C语言—总结4—算法效率：代码，场景

一.时间复杂度

    1. 定义：衡量算法的运行速率。 一个算法所花费的时间与其语句的执行次数成正比。

       例1：

                   

     执行次数： F(N)=N^2;              时间复杂度：  O(N)=N^2;

     例2：

                   

            执行次数： F(N)=N^2+N;              时间复杂度：  O(N^2);     

          2.推导时间复杂度的方法：

                <1>. 用常数1取代运行时间中的所有假发常数

                <2>. 只保留最高阶项

                <3>. 如果最高阶项不是1，去除与之相乘的常数。             

         3.时间复杂度大小排序

            O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

 二.空间复杂度

            1.定义：衡量算法所需的额外空间。 对一个算法在运行过程中临时占用储存空间大小的亮度。

           2.  创建常数个变量：O(1);

                创建N个变量：O(N);

       例1. 

                 

                     空间复杂度：O(1);

             例2.  

 空间复杂度：因为没有开辟额外的空间，所以空间复杂度为：O(1);

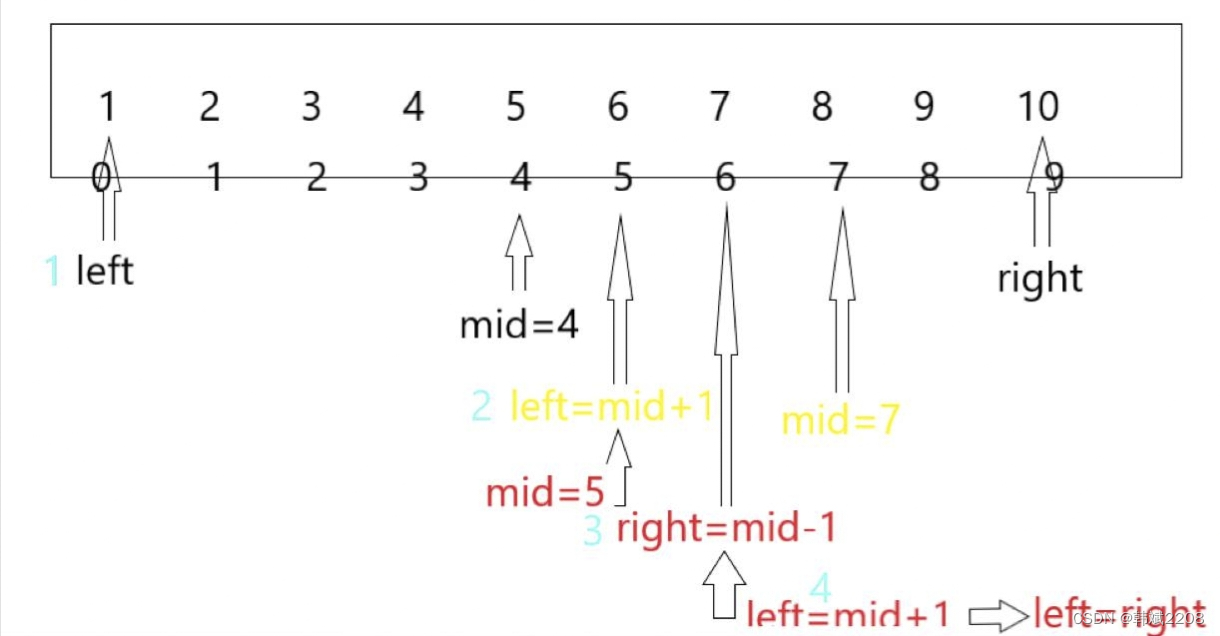
三.  二分查找

      1. 要求：<1>. 必须采取顺序存储结构

                  <2>. 时间复杂度：O(logn);

                  <3>. 空间复杂度：O(1);

       2.求中间数字

                    奇数： 

                       

               偶数：

                         

      3. 代码：

              

 

4. 过程