汉诺塔(hanoi)问题从0到1详解

文章目录

一、汉诺塔问题的起源

二、汉诺塔问题的实现

 一、汉诺塔问题的要求

​二、汉诺塔思路从易到难

1、一个盘子的实现

 2、两个盘子的实现

3、三个盘子的实现

4、 n个盘子的实现

三、汉诺塔代码的实现

四、尾言

---

 

标题：汉诺塔问题详解

作者：@Ggggggtm

寄语：舞台再大，你不上台，永远是观众

一、汉诺塔问题的起源

  有没有人会和我一样，看到这个问题就会想到这个问题是怎么形成的呢？是谁提出来的呢？或者是来源是呢？于是我查询了一下，跟大家简单叙述一下。 

  传说在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。 

   当然，如果真的要是把64片金片由一根针上移到另一根针上，并且始终保持上小下大的顺序。那么到底要移多少次呢？假如一秒移一次，还是每一次都移的是正确的前提下，要移动多长时间呢？也就是传说的移动结束后世界就会消灭，那我们来看看到底还有多长时间世界会消灭！

 二、汉诺塔问题的实现

 一、汉诺塔问题的要求

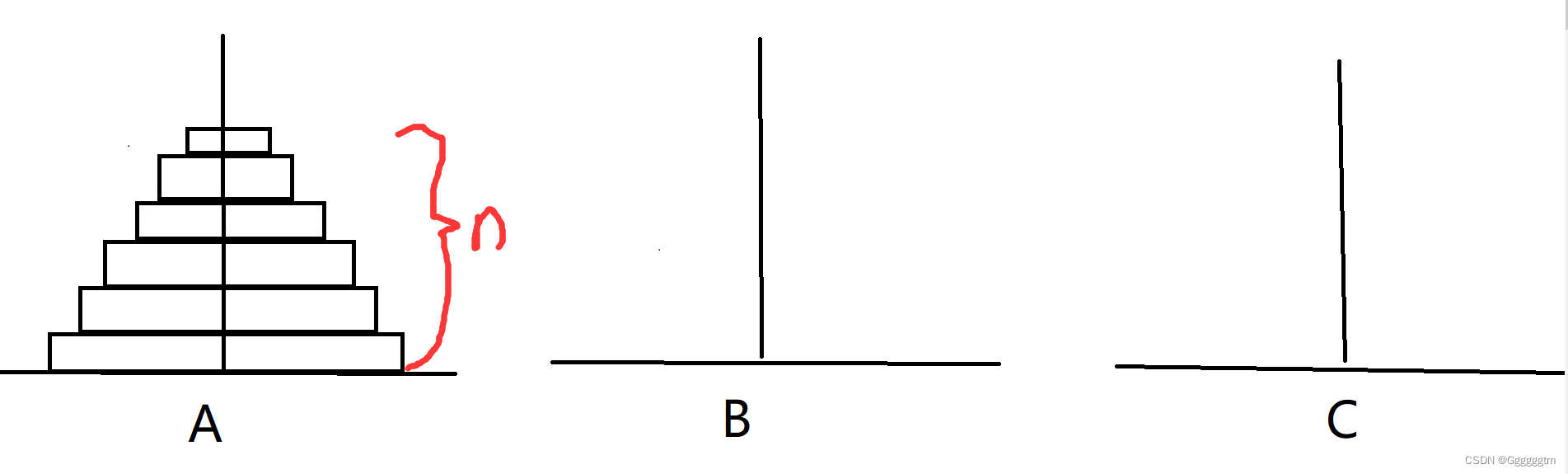
  如下图，把A柱子上的盘子借助B柱子移动到C柱子上面。移动的要求：每一步只能移动一个盘子，同时必须满足大盘子在小盘子的下面。我们先从简单的开始一步一步分析。

 二、汉诺塔思路从易到难

1、一个盘子的实现

    当只有一个盘子的时候很简单，直接从A移动到C上。如图： 

 2、两个盘子的实现

   当有两个盘子的时候，我们就要借助B柱子了。接下来，我将移动的步骤直接简化表达。

1. A->B
2. A->C
3. B->C

 第一步：

第二步：

 

 第三步：

   第三步移动结束后就算完成了。 

3、三个盘子的实现

   我么你来看一下三个盘子的实现，A->C,A->B,C->B,A->C,B->A,B->C,A->C. 

如图：

第一和第二步：

 第三步：

第四步：

   注意！！！！！！

   到这里我们先简单总结一下：我们移动的思路其实就是先把除了最下面的盘子，也是就上面的两个盘子借助柱子C移动到柱子B上，然后我们再把最下面的盘子直接移动到柱子C上，最后我们只需要把柱子B上的盘子借助柱子A 移动到柱子C上即可。

  第五和第六步：

 第七步：

 总览图：

 

  到这里我们就移动和结束了。 

4、 n个盘子的实现

  我们来看一下n个盘子的实现思路。总上我们可以总结出：当有n个盘子的时候，我们先把除了最底下的盘子之外的n-1个盘子借助柱子C移动到柱子B上，然后再把最后一个盘子移动到柱子C上。到这里我们只需要将柱子B上的n-1个盘子借助柱子A移动到柱子C上即可。

  如图：

第一步：

第二步：

第三步：

   归根结底，我们上面用到了把大化小，从而一步一步解决的思想。这不就是递归吗！我们来看一下代码的实现。可以结合着代码一起理解一下哦。

 三、汉诺塔代码的实现

#include<stdio.h>
void move(char pos1, char pos2)
{
	printf("%c->%c ", pos1, pos2);
}
void hanoi(int n, char A, char B, char C)
{
	if (n == 1)
		move(A, C);
	else
	{
		hanoi(n - 1, A, C, B);//n-1个盘子从柱子A通过柱子C移动到柱子B上
		move(A, C);           //最底下的盘子移动到C上
		hanoi(n - 1, B, A, C);//n-1个盘子从柱子B通过柱子A移动到柱子C上
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	hanoi(n, 'A', 'B', 'C');
	return 0;
}

四、尾言

  通过上面的规律我们可以看出：假设有n片，移动次数是f(n).显然f(1)=1,f(2)=3,f(3)=7，且f(k+1)=2*f(k)+1。此后不难证明f(n)=2^n-1。n=64时，假如每秒钟一次，还是移动正确的情况下，共需多长时间呢？一个平年365天有31536000 秒，闰年366天有31622400秒，平均每年31556952秒，计算一下：18446744073709551615秒，这表明移完这些金片需要5845.54亿年以上，而地球存在至今不过45亿年。太阳系的预期寿命据说也就是数百亿年。

  要是僧侣们预言是准确的，那我们何乐而不为呢？当然，预言终究是是预言，我们这个时代还是要讲究科学依据的。

  好了，汉诺塔的问题我们就讲解到这里，希望这篇文章对你很好的帮助，感谢阅读！