量子计算的基本运算：Hadamard 门、CNOT 门、Pauli 门详解

量子计算是现代计算科学的前沿领域，它与经典计算机在处理信息的方式上有着本质的区别。量子计算机利用量子比特（qubit）的叠加态和量子纠缠等特性来进行计算，从而在某些特定任务上超越传统计算机。量子计算的核心运算单元是量子门，它们通过作用于量子比特来操控量子状态。本文将详细介绍三个基础的量子门：Hadamard 门（H 门）、CNOT 门（Controlled-NOT 门） 和 Pauli 门，并对它们的工作原理、数学描述以及在量子计算中的应用进行深入讲解。

1. Hadamard 门（H 门）详解

定义与作用

Hadamard 门（通常用符号 H 表示）是量子计算中一个非常重要的单比特门。它的主要作用是将量子比特从基础的确定性状态（|0⟩ 或 |1⟩）转换到叠加态，即将量子比特的状态同时“分配”到多个可能的结果。Hadamard 门广泛应用于创建量子叠加态，通常作为量子算法的初始步骤。

在量子比特的状态空间中，Hadamard 门的作用是将比特的状态变成两个基态的均匀叠加。

数学表示

对于单个量子比特状态 |0⟩ 或 |1⟩，Hadamard 门的作用如下：

这表示，当 Hadamard 门作用于 |0⟩ 状态时，量子比特会变为 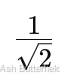的叠加态，分别包括 |0⟩ 和 |1⟩。对于 |1⟩ 状态，Had