CSP初赛基本信息(书接上回)

一、逻辑运算

逻辑运算一共有三种，每种都有两种写法：
逻辑非：!
逻辑与：&&
逻辑或：|| 

二、逻辑运算的优先级

非>与>或

三、位运算+逻辑运算的优先级

逻辑非(!)=按位反(~)>位移运算(<<,>>)>不等号（>=,<=）>等号（==,!=）>按位与（&）>按位异或（^）>按位或（|）>逻辑与（&&,^）>逻辑或 （||)

四、逻辑表达式

由逻辑运算复合而成，只有两种结果：true和false，在C/C++中，返回的值以0表示假，以
1表示真。

五、条件表达式(三目运算)

条件表达式的基本形式如下：
<表达式1>？<表达式2>：<表达式3> 

若果表达式1为真，就返回表达式2，否则返回表达式3

(define:#define 表达式1 表达式2表示 表达式1为表达式2)

注意：如果条件表达式有多个进行复合，那么在执行的时候需要从由往左依次判断最后得出一个结
果。即：右结合性。
比如:
<表达式1>？<表达式2>：<表达式3>？<表达式A>：<表达式5>
那么，在执行的时候是从3开始判断是否为真，然后执行某一个表达式，依次向上回溯。

六、图论理论知识

完全图：任意两点都有边相连，我们很容易推出来，一张完全图的边数为（n为节点个数)n*(n-1)
连通图：顾名思义，连通图就是连通的图，即任意两点都能直接或间接到达，这就区别于完全图
必须直接用边到达的定义。

树：直观来讲，就是一张长得像树的图。定义是任意两点之间的简单路径有且只有一
条。树是一棵连通且无环的图。它的边数是n-1。

七、二叉树的遍历

二叉树有不同的遍历方式，一般来讲，我们将其分成三类：先序遍历（也叫先根遍历）、中序遍历
（中根遍历）以及后序遍历（后根遍历）。 

先序遍历：遍历方式如下：根—左儿子一右儿子。

中序遍历：遍历方式如下：左儿子—根—右儿子。

后序遍历：遍历方式如下：左儿子一右儿子一根

 

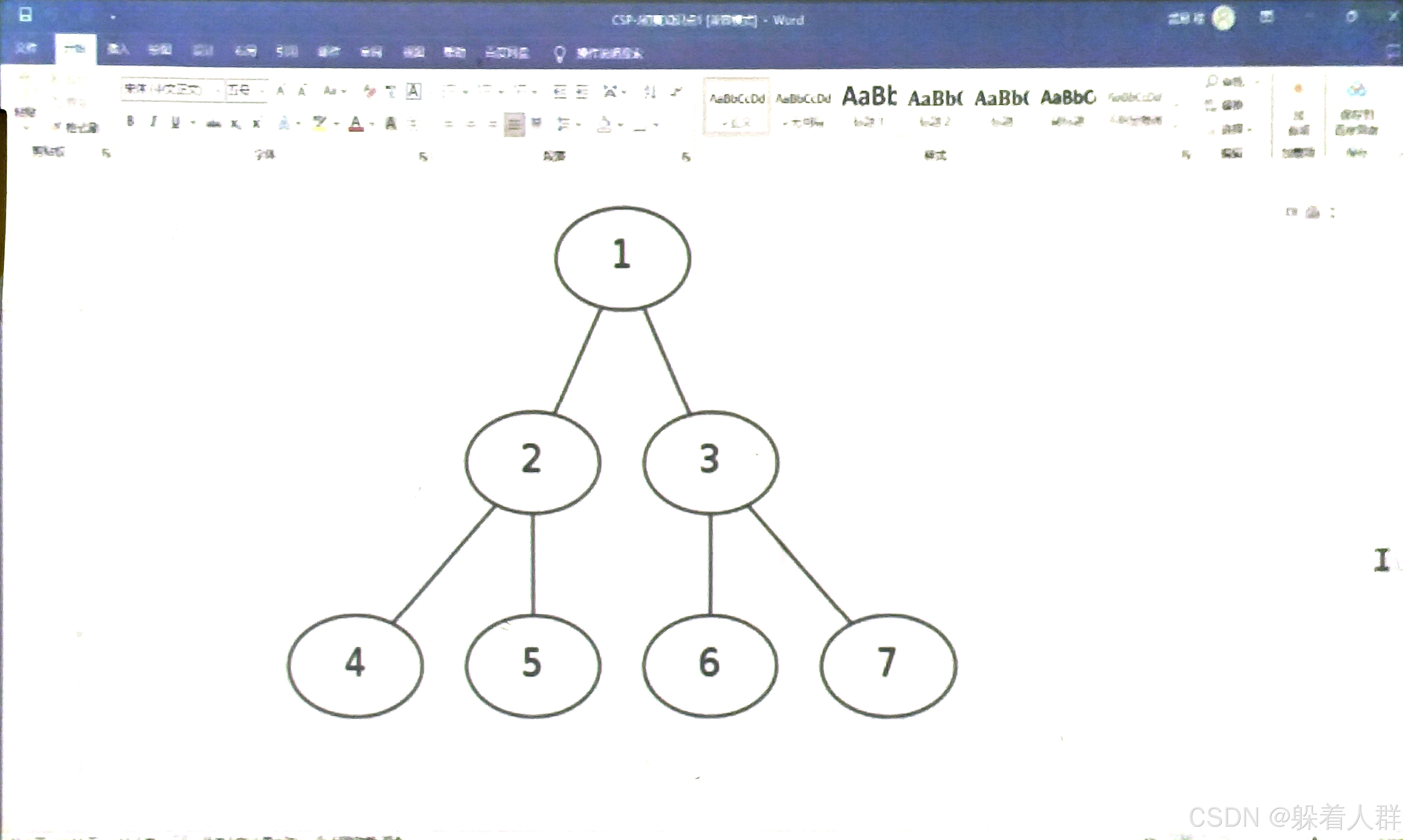
这张图的三种遍历

先序遍历：1245367
中序遍历：4251637
后序遍历：4526731

 一个推论:
先序遍历+中序遍历＝一棵确定的二叉树
后序遍历+中序遍历＝一棵确定的二叉树
先序遍历+后序遍历=啥也不是

已知两种遍历，求第三种遍历(求后续遍历)

#include <bits/stdc++.h>
using namespace std;
string inorder,preorder;
void Postorder(int pre_f,int pre_l,int in_f,int in_l) {  //pre为前序遍历 in为中序遍历
    if(pre_f>pre_l||in_f>in_l){
		return;
	}
    int root_point=inorder.find(preorder[pre_f]);//根左右
    Postorder(pre_f+1,pre_f+root_point-in_f,in_f,root_point-1);//pre_f+1左子树根节点
	//左子树的节点数等于中序遍历中根节点位置之前的节点数root_point - in_f 
    Postorder(pre_f+root_point-in_f+1,pre_l,root_point+1,in_l);//右子树
    cout<<preorder[pre_f];
}
int main(){
    cin>>inorder>>preorder;
    int l=inorder.length()-1;
    Postorder(0,l,0,l);
    return 0;
}

求先序遍历

#include <iostream>  
#include <string>  
using namespace std;  

string preorder;  // 存储先序遍历的结果  
  
// 递归函数，根据中序遍历和后序遍历构建二叉树，并输出先序遍历  
void buildPreorder(string inorder, string postorder, int inStart, int inEnd, int postStart, int postEnd) {  //inorder 中序post order后序 
    if (inStart > inEnd || postStart > postEnd) return;  //instart和inorder对应序的边界（字符串长度） 
  
    // 后序遍历的最后一个元素是当前子树的根  
    char root = postorder[postEnd];  
    preorder += root;  // 添加到先序遍历结果中  
  
    // 在中序遍历中找到根的位置  
    int rootIndex = inStart;  //rootIndex 
    while (inorder[rootIndex] != root) rootIndex++;  
  
    // 递归构建左子树和右子树  
    int leftSubtreeSize = rootIndex - inStart;  
    buildPreorder(inorder, postorder, inStart, rootIndex - 1, postStart, postStart + leftSubtreeSize - 1);
    buildPreorder(inorder, postorder, rootIndex + 1, inEnd, postStart + leftSubtreeSize, postEnd - 1);
}  
  
int main() {  
    string inorder, postorder;  
    cin >> inorder >> postorder;  
  
    // 调用递归函数构建先序遍历  
    buildPreorder(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);  
  
    // 输出先序遍历结果  
    cout << preorder << endl;  
  
    return 0;  
}

特殊二叉树及其性质
完全二叉树：只有最后一层不是满的，且最后一层的所有节点均集中在左侧。

特殊二叉树的性质：
1、对于一棵完全二叉树来讲，它的叶子节点为n，则节点总数为2×n-1。此结论可逆。
2、对于一棵满二叉树来讲，它的层数（深度）为k，则它的节点总数为2k-1。此结论可逆。

八、拓扑排序

不会

拓扑排序是一种对有向无环图（DAG）进行排序的算法。

它的主要思想是：对于一个有向无环图，选择一个入度为 0 的顶点并将其输出，然后删除该顶点以及与其相关的边，重复这个过程，直到图中所有顶点都被输出。

以下是一个简单的拓扑排序的示例：

假设有一个有向无环图，顶点表示任务，边表示任务之间的先后关系。

顶点：A、B、C、D、E

边：A -> B，A -> C，B -> D，C -> D，D -> E

首先，找到入度为 0 的顶点，即 A 。输出 A ，然后删除 A 及其相关的边，此时 B 和 C 的入度变为0 。接着，选择 B 输出，删除 B 及其相关的边，此时 D 的入度变为 0 。然后，输出 C ，再输出 D ，最后输出 E ，完成拓扑排序。需要注意的是，如果一个图不是有向无环图，那么就无法进行拓扑排序。

九、简单数据结构基本理论

1、栈
想象一个桶，你从上面往里扔砖，然后你想把某一块砖拿出来，你需要先拿出来你后扔进去的砖。
这就是栈。栈的基本原则是：后进先出
附：前、中、后缀表达式
https://www.cnblogs.com/fusiwei/p/11615499.html
2、队列
想象你在排队买票，这个队伍中的人都非常有素质，都自觉排队而且不会提前离开队伍。这样就只
能从队首买完票再离开，从队尾进入队伍。队列的基本原则是：先进先出。
再来一发图示:

十、链表

链表分两种：单向链表和双向链表.
https://www.cnblogs.com/fusiwei/p/11387165.html

十一、字符串

字符串子串的概念：字符串是一串字符（废话），它的子串被定义为：字符串中任意个连续的字符
组成的子序列。
字符串子串个数的计算公式：
（就是字符串长度等差数列) 

十二、时、空复杂度的计算

时间复杂度：渐进时间复杂度用符号0 表示。一个程序的语句执行次数可以用一个代数式表示，那么我们取这个代数式的最高次项且忽略此项系数作为时间复杂度。如果一个程序的语句执行次数为2n^3+3n^2+n+7，那么这个程序的渐进时间复杂度为O(n^3)。
计算非递归程序的时间复杂度：简单粗暴，数循环。
1.常数：常数即为我们忽略掉的O中最高次项的系数与低次项所带来的时间消耗。
2.空间复杂度：类比时间复杂度。看开空间开了多大。
*计算空间占用量：根据我们以上说过的计算机存储单位的知识：一个int占用的内存是4B，所以
我们把开的int乘上4，再除以1024就是KB，同理，再除1024就是MB.
公式：n为元素个数，M为最终答案（以MB为单位)

PS:一般来讲，比赛中所给的256MB内存可以开 6×10的7次方个int类型的变量。另外，大数组必须开全局变量。如果扔在主函数里极容易爆栈。