手把手拆解排序算法（计数排序、桶排序、基数排序）

最新推荐文章于 2025-04-11 19:41:22 发布

搞程序的心海

最新推荐文章于 2025-04-11 19:41:22 发布

阅读量924

点赞数 20

文章标签：排序算法算法数据结构

本文链接：https://blog.youkuaiyun.com/weixin_66485800/article/details/146150865

版权

嗨，大家好，这是排序算法第 8 篇文章，其它算法详细分析，可前往合集查看！

一、计数排序

1. 算法介绍

计数排序是唯一不需要元素比较的排序算法，通过统计元素出现次数完成排序。适用于整数数据且数据范围较小的情况（如年龄排序、考试成绩排序）。

2. 原理分析及代码实现

核心步骤：

统计每个元素出现次数
计算元素累计分布
反向填充有序数组

流程演示如下

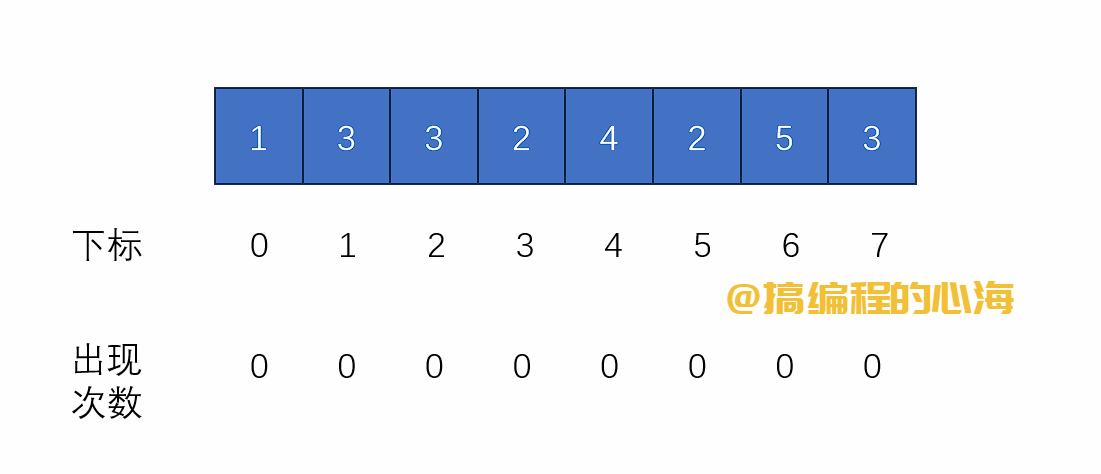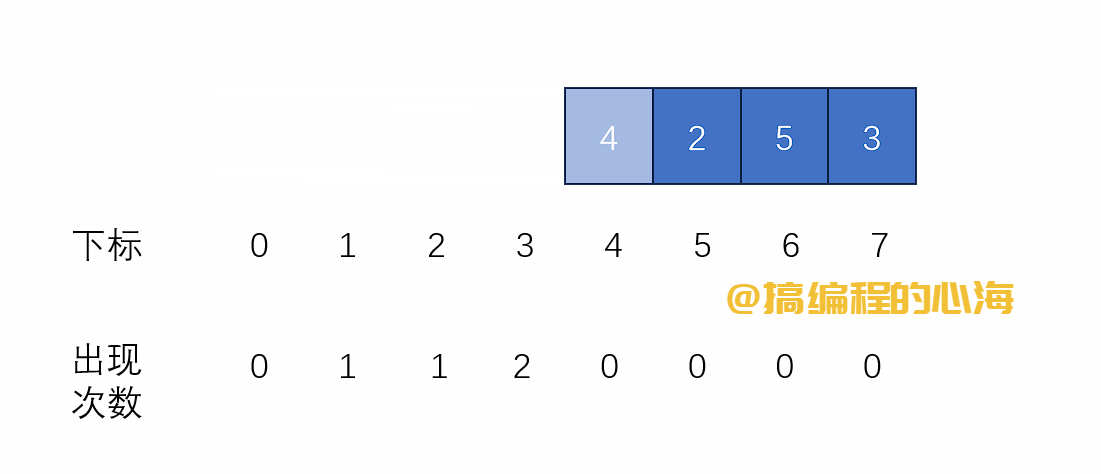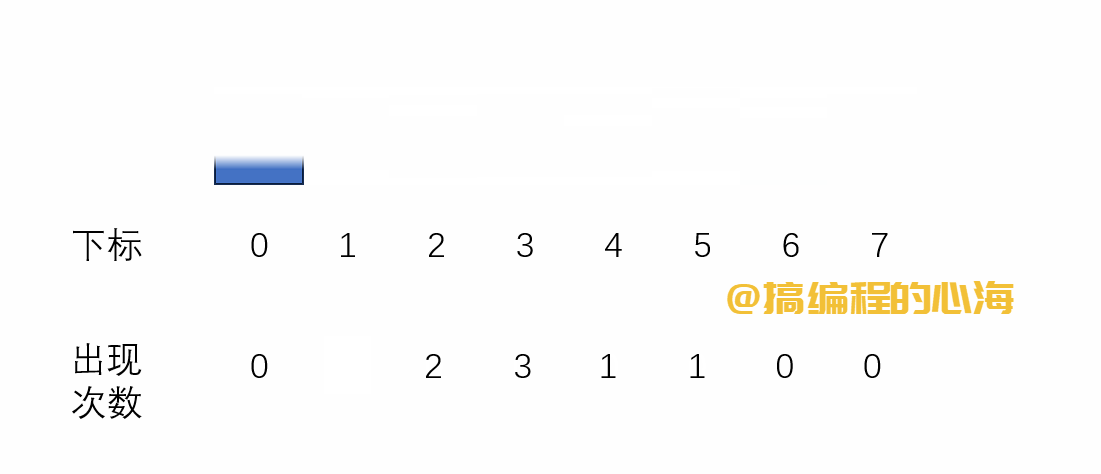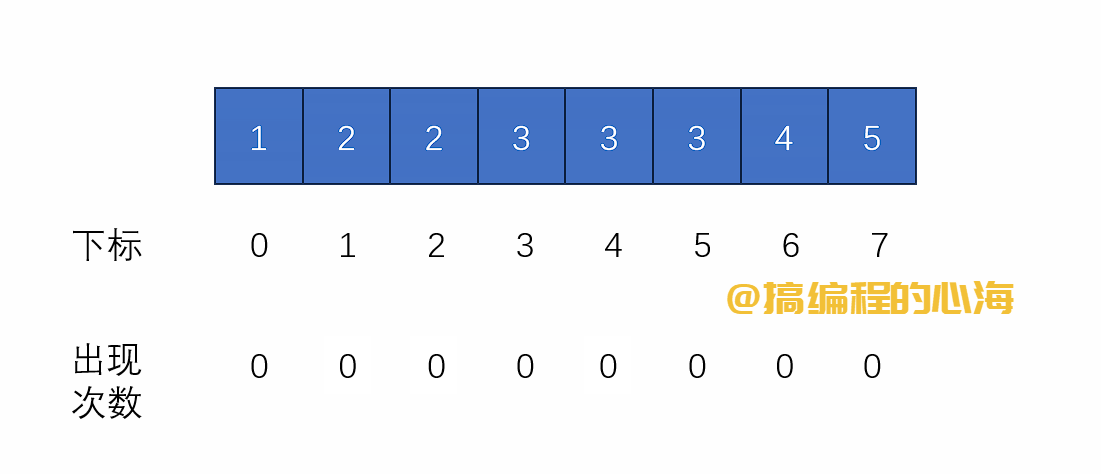
基础版本代码如下

# 计数排序函数（基础版）
def count_sort(li, max_num):
    # 创建计数数组（长度=max_num+1，包含0~max_num的所有可能值）
    # 例如max_num=10时，可统计0-10共11个数字的出现次数
    count = [0 for _ in range(max_num + 1)]  
    
    # 统计元素出现频率（时间复杂度O(n)）
    for val in li:
        count[val] += 1  # 直接以元素值作为索引统计
    
    # 清空原列表准备重建有序数据
    li.clear()
    
    # 根据计数数组重构有序列表（时间复杂度O(k)，k为max_num+1）
    for index, val in enumerate(count):
        # 将当前数值重复添加val次（val是该数字出现的次数）
        # 例如count[5]=3时，会向列表添加三个5
        for i in range(val):
            li.append(index)

因为计数排序并不太常用，局限性也比较大，这里就给出基础版代码，不再进一步优化（比如说 count 列表范围，这里我们假设数据是 0 到 max_num ，没有负数等等情况）

3. 算法分析

从上一节的代码可以看出，计数排序需要重新新建一个空列表，并且我们需要知道我们数据的长度，所以它就会有比较大的局限性

时间复杂度

我们前面的代码，新建的数组假设长度为 k ，原数组长度 n ，第二个 for 循环执行 n 次，所以时间复杂度为 O(n+k)，虽然时间复杂度快，但是计数排序无法处理小数，总不可能说1.1 1.11 这些小数，一个数占一个位置，没法处理

空间复杂度

我们额外建一个长度 k 的列表，所以空间复杂度为 O( k )

当我们处理的数据量很小，而范围很大，那么我们重新建一个列表就很浪费空间，比如只有5个数，但是范围是 0 到 1 亿，那我们建一个这么长的列表是不是太浪费空间了？

4. 小结

优点：线性时间复杂度，适用于小范围整数；
缺点：数据范围过大时空间浪费严重，无法处理浮点数或字符串

二、桶排序

1. 算法介绍

桶排序是计数排序的优化版，将数据分到有限数量的桶中，每个桶单独排序后合并。其特点包括：

适用于分布均匀的数据（如学生成绩、年龄）；
通过分桶降低数据规模，提升排序效率

2.算法原理及实现

步骤：

（1）分桶：根据数据范围确定桶的数量，将元素分配到对应桶中

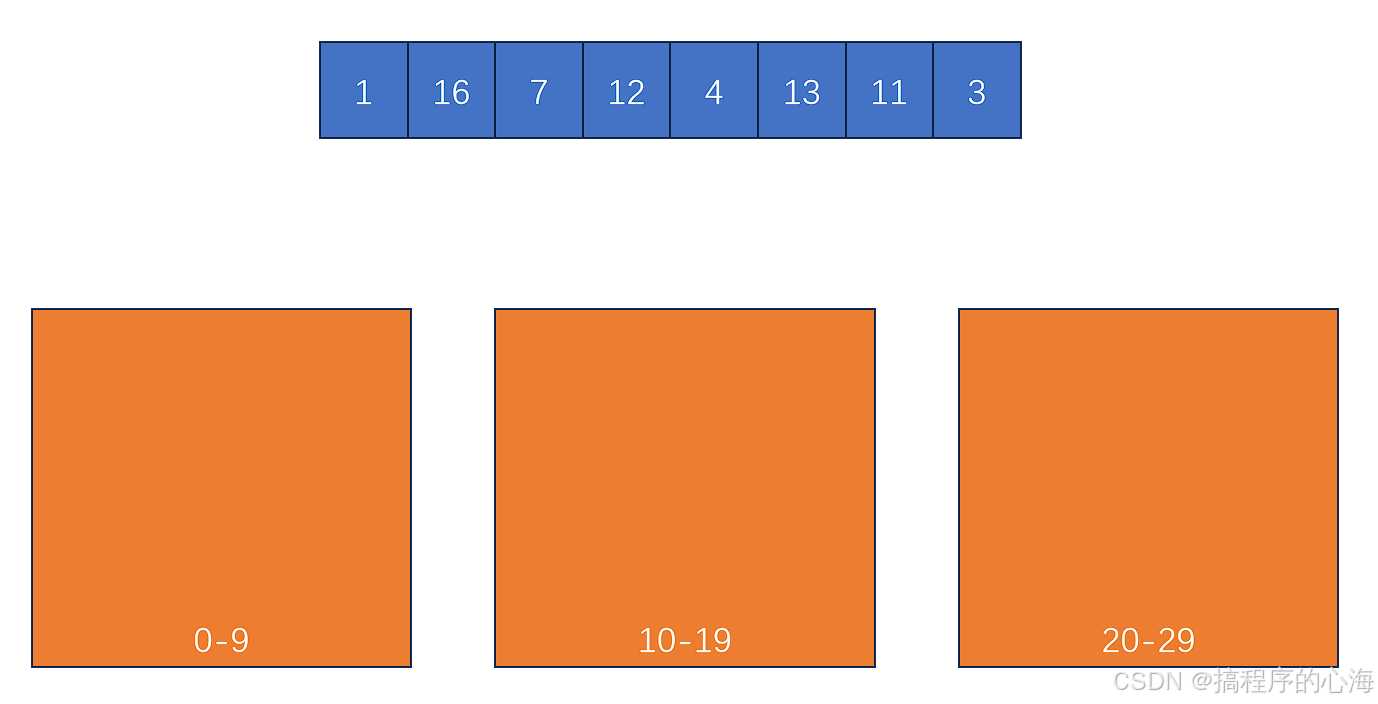
（2）桶内排序：对每个桶使用其他排序算法（如插入排序）

（3）合并结果：按桶顺序合并所有元素

当然，我们也可以在元素入桶的同时进行排序，效果也是一样的，例如下方代码

def bucket_sort(li, n=100, max_num=10000):
    buckets=[[] for _ in range(n)]
    for var in li:
        i =min(var // (max_num // n),n-1)# i 表示var放到几号桶
        buckets[i].append(var)#把var加到桶里
        for j in range(len(buckets[i])-1,0,-1):#插入排序
            if buckets[i][j]<buckets[i][j-1]:
                buckets[i][j],buckets[i][j-1] = buckets[i][j-1],buckets[i][j]
          	else:
                break
     	sorted_li=[]
        for buc in buckets:
            sorted_li.extend(buc)
      	return sorted_li

这个代码就是假设默认最大数是 10000，然后 100 个桶，这里的第四行 i 的计算使用 min ，是为了确保 10000 以及比它大的数字，最后我们放入99号桶，其实桶在这里就是我们的一个列表，然后元素进入对应桶后，使用插入排序，确保列表有序，最后按顺序汇入一个空列表即可

3. 算法分析

时间复杂度：平均O(n + k)，最坏O(n²k)（取决于桶内排序算法）
空间复杂度：O(nk)，需存储桶和结果数组

4. 小结

优点：优化计数排序的数据范围限制，适合均匀分布的大规模数据，如果分布不均，比如100个桶，但是大部分数据在一个桶里，那么这个桶就会在排序上小号大量时间
缺点：数据分布不均时效率下降，桶数量和大小需合理选择

三、基数排序

1.算法介绍

基数排序通过按位分配和收集实现排序，分为LSD（最低位优先）和MSD（最高位优先）两种方式。其核心特点：

适用于多位数整数或字符串（如手机号、日期）
每次按某一位分配到桶中，重复多次直到最高位

2.算法原理及实现

基数排序类似我们生活中的多关键字排序，比如说班级成员按总成绩降序排序，总成绩相同某一科目成绩高的排名靠前

排序演示如下

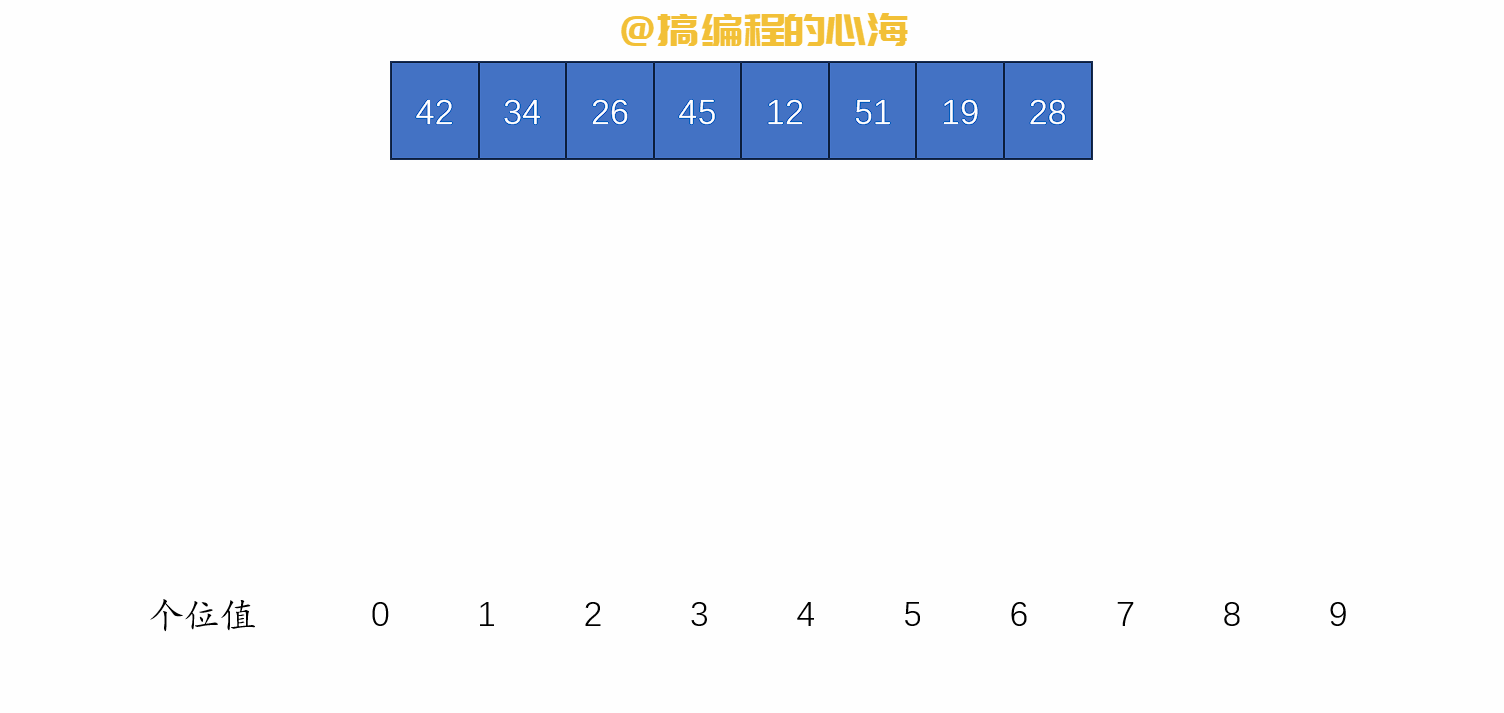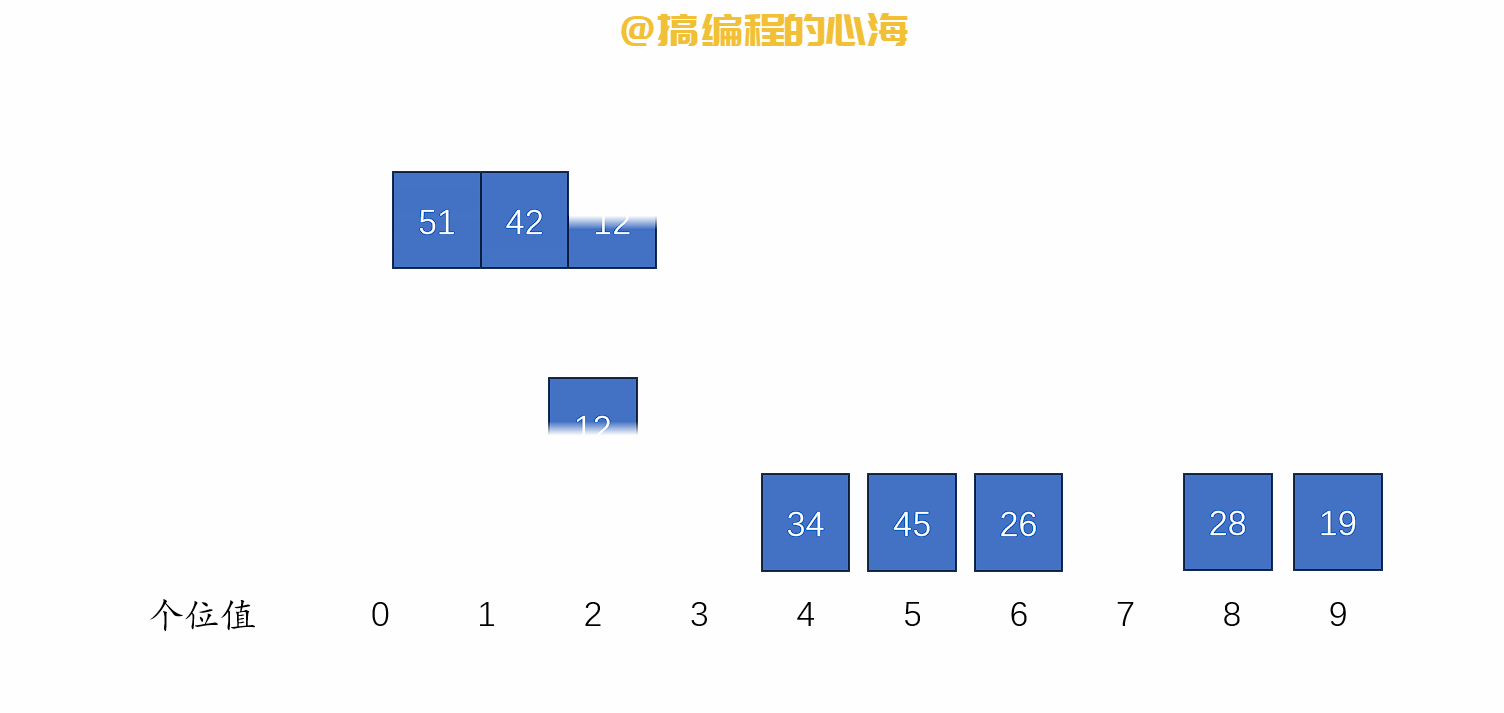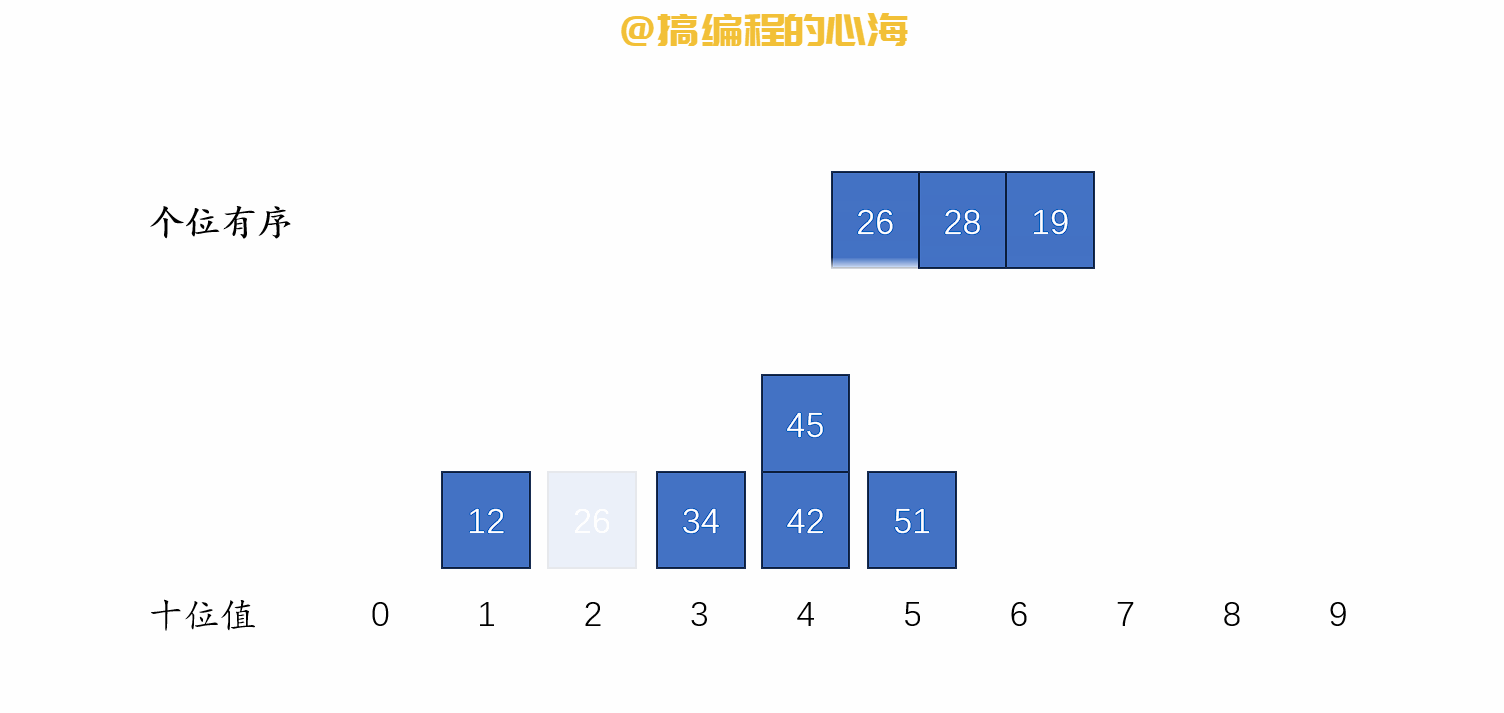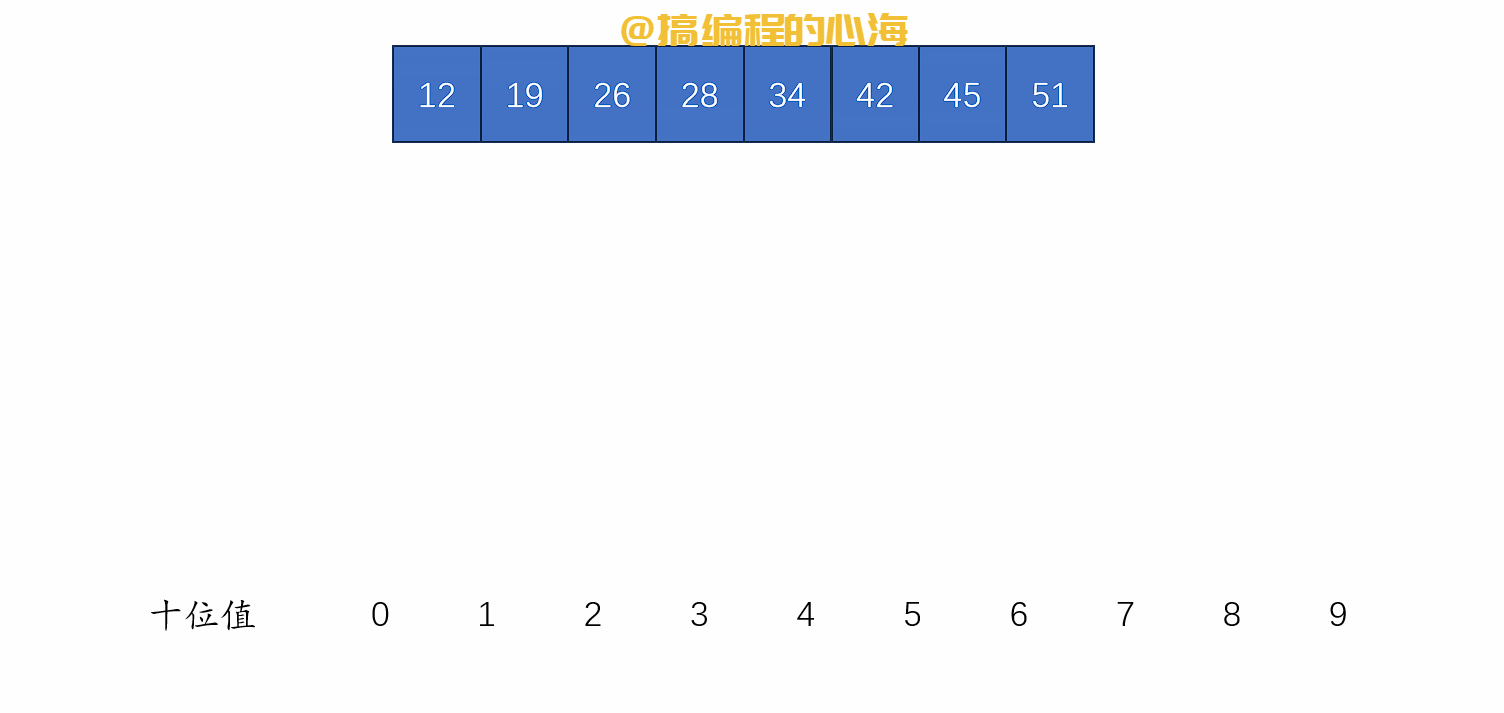
def radix_sort(li):
    # 1. 确定最大值以计算最高位数
    max_num = max(li)  # 获取列表中最大值，用于终止循环条件
    
    it = 0  # 当前处理的位数（0表示个位，1表示十位...）
    
    # 2. 按位数循环处理（直到覆盖最大值的最高位）
    while 10**it <= max_num:  # 当10^it超过max_num时，说明所有高位已处理完毕
        
        # 3. 创建10个空桶（对应数字0-9）
        buckets = [[] for _ in range(10)]  
        
        # 4. 按当前位数分配元素到桶中
        for var in li:
            digit = (var // (10**it)) % 10  # 提取当前位的数字
            buckets[digit].append(var)  # 将元素放入对应桶
            
        # 5. 清空原列表并按桶顺序重构列表
        li.clear()
        for buc in buckets:
            li.extend(buc)  # 按0-9桶顺序合并元素
        
        # 6. 处理下一位数
        it += 1

步骤1：通过max_num确定需要处理的位数（例如max_num=325时需处理3位）
步骤2：外层循环按位迭代（个位→十位→百位...）
步骤3-4：按当前位数字分配元素到桶（类似扑克牌按花色分组）
步骤5：合并桶时保持桶0-9的顺序（确保低位排序结果被高位排序保留）
步骤6：迭代处理更高位，直到覆盖最大数的所有有效位

3.算法分析

时间复杂度

从前面代码可以看出，其时间复杂度与最大位数有关，假如最大为 k 位数，数组长度 n，则时间复杂度为 O(kn)

空间复杂度

这里因为有额外的数组，空间复杂度为 O(k+n)

4. 小结

优点：适用于多位数数据，时间复杂度与数据规模线性相关；
缺点：需明确位数，对非整数类型需额外处理

四、总结

关系与演进：
- 计数排序是桶排序的特例（每个桶对应一个数值）
- 桶排序通过分桶降低数据规模，而基数排序通过多次分桶处理多位数问题
适用场景：
- 计数排序：小范围整数，如年龄、成绩
- 桶排序：均匀分布的浮点数或字符串
- 基数排序：多位数整数（如身份证号、电话号码）
核心权衡：
计数排序速度快但空间消耗大，桶排序依赖数据分布，基数排序需明确位数