手把手拆解三大基础排序算法（选择排序）

嗨，大家好，我是心海，这是我2025年第 2 篇文章，未来大家相互学习，文章若有不足，欢迎指正！

目录

一、算法简介

二、算法原理及实现

三、算法时空复杂度分析

四、总结

---

一、算法简介

选择排序是一种简单直观的排序算法。它的基本思想是：

每一次从待排序的数据中选出最小的一个元素，存放在序列的起始位置；

然后，再从剩余未排序元素中继续寻找最小元素，放到已排序序列的末尾。以此类推，直到所有元素都排好序（若降序排列则相反，寻找最大元素）。

二、算法原理及实现

选择排序原理非常简单

例如下面这个数组

每一轮遍历，从无序区第一个数据开始，将该数据标记为最小值，同时标记该位置，然后向后遍历，依次和目前最小值比较，我们这一轮就可以找到最小值 4 ，那么它和我们标记的位置，也就是原来 7 的位置交换一下就完成了。

完整的一轮动画演示如下：

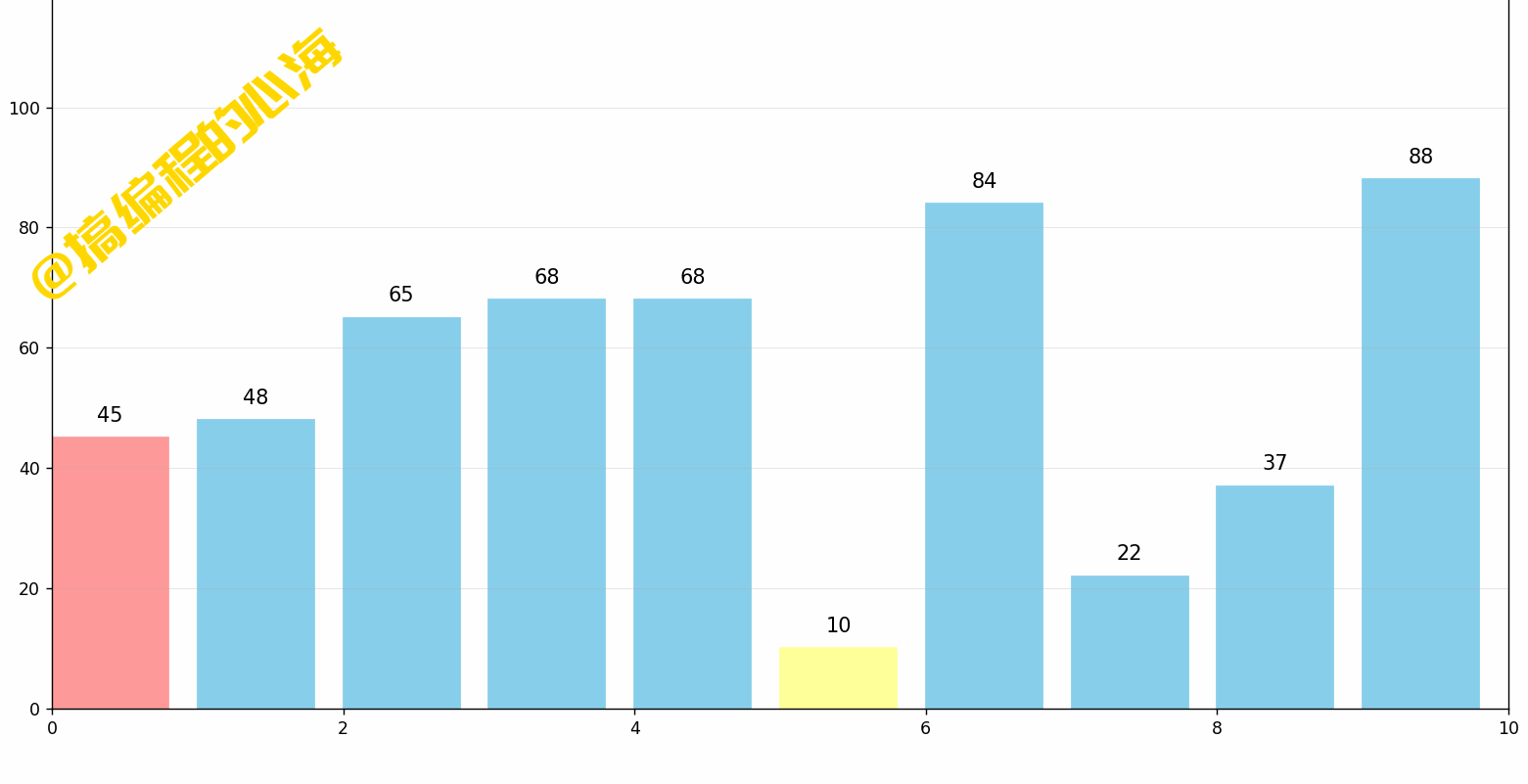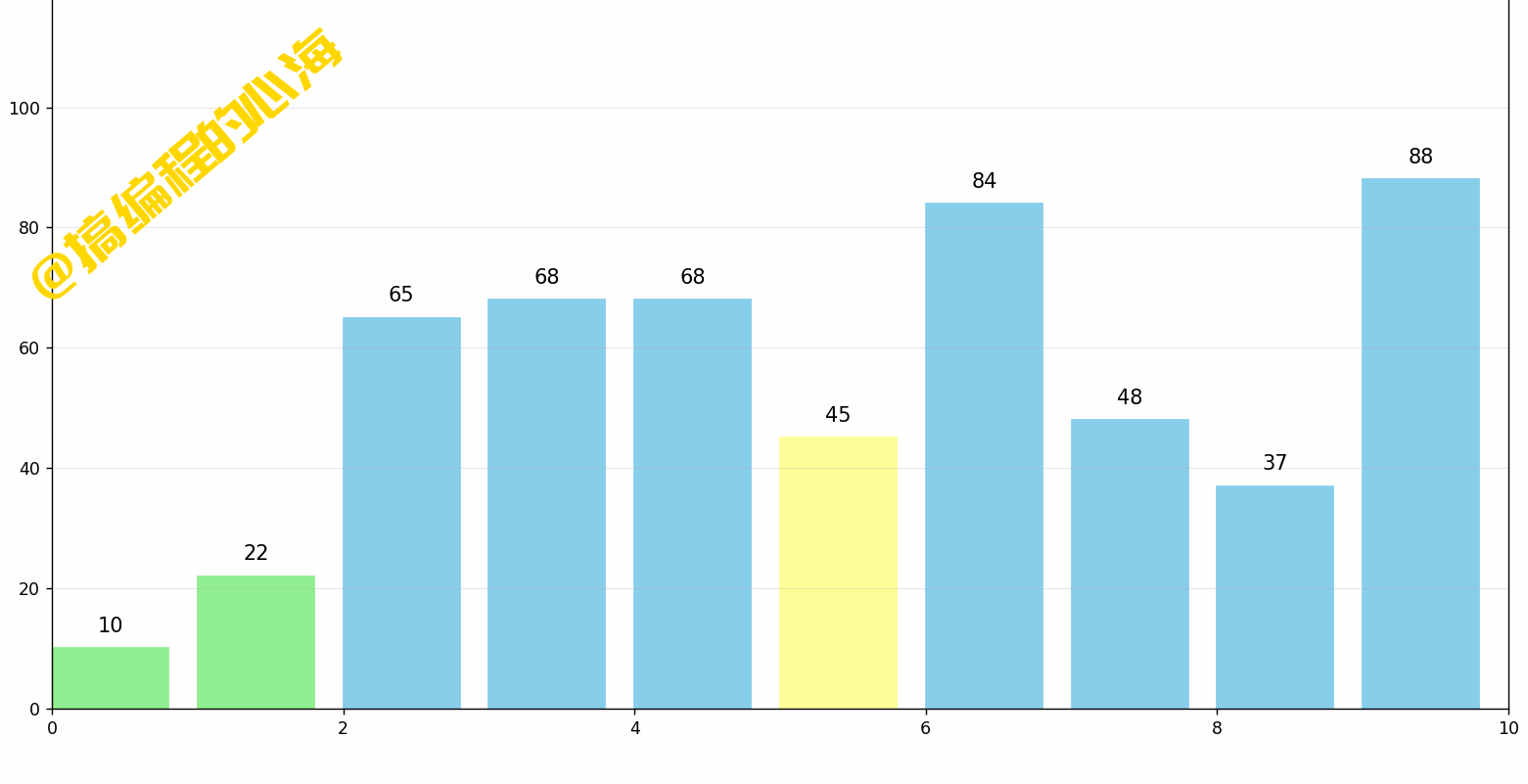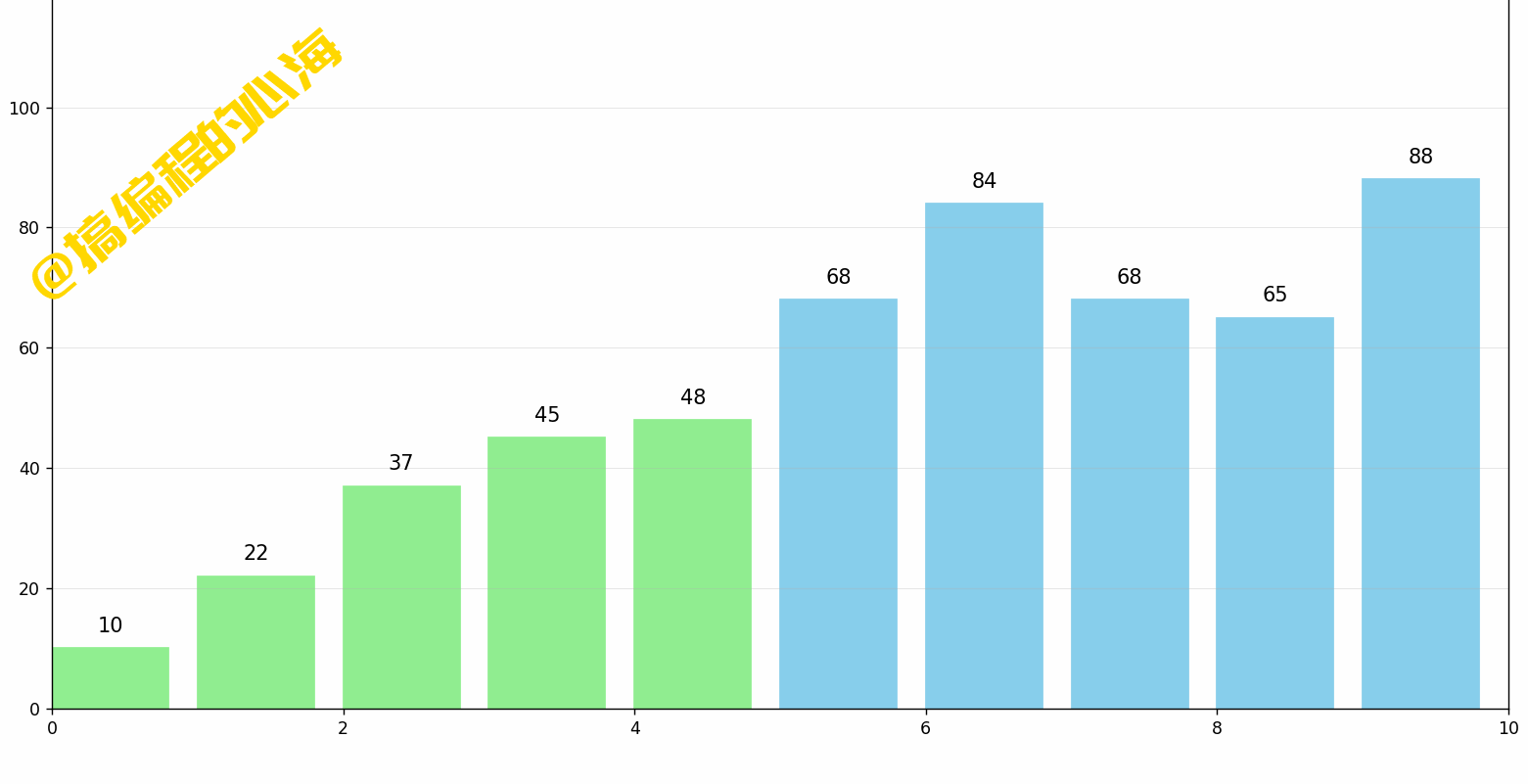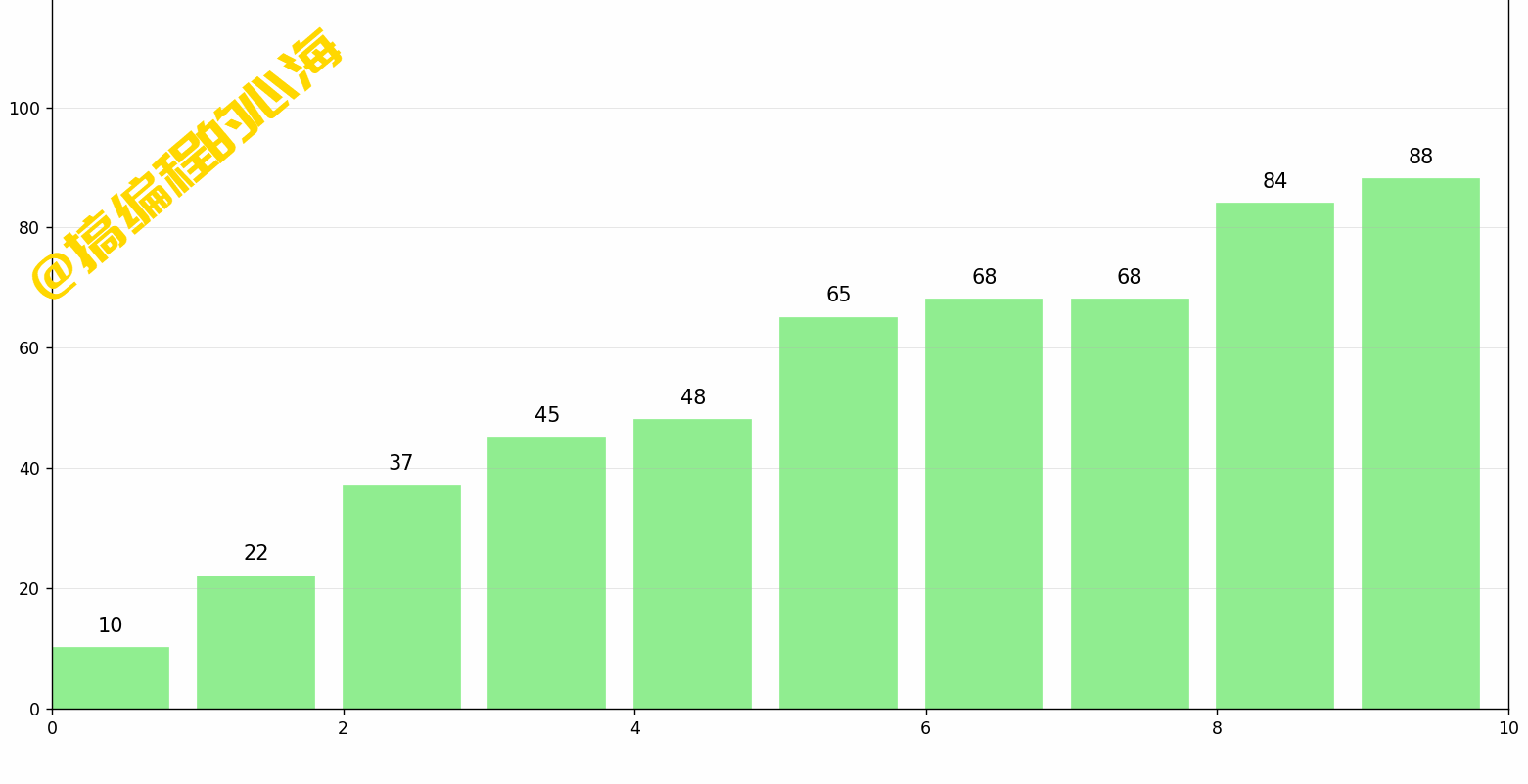
那么思考一下，我们选择排序需要遍历几趟？每一趟需要从第几个数据开始寻找最小值？

首先，每一趟排序，有序区就增加一个元素，那么n-1躺后，有序区就有n-1个元素，而无序区只有1个元素，那么此时整个数组就是有序的了，也就是需要总共n-1躺排序；

先看完整代码

def select_sort(li):
    for i in range(len(li)-1):#第i躺
        min_loc=i
        for j in range(i+1,len(li)):
            if li[j]<li[min_loc]:
                min_loc=j
        li[i],li[min_loc]=li[min_loc],li[i]

而第i躺（i从0开始）遍历结束，有序区就有i+1个元素，也就是说第i躺遍历开始时有序区有i个元素，那么无序区第一个元素下标也就是i

我们用一个变量 min_loc 保存无序区第一个值的下标，那么我们比较时，j 就可以从无序区第二个下标开始，也就是从i+1开始，直到无序区最后一个元素（下标n-1）

而在后续遍历时，如果我们遇到元素值小于当前最小值，就将下标赋值给min_loc，最后遍历完这一趟，将最小值与无序区第一个元素交换即可

三、算法时空复杂度分析

时间复杂度

选择排序不像我们前面的冒泡排序，我们不会提前终止，所以无论数组是什么情况，都要遍历n-1躺，每一趟遍历n-i-1次，时间复杂度为O(n²)

空间复杂度

和前面冒泡排序一样，选择排序没有生成新的数组，只使用一个额外变量min_loc，故空间复杂度为O(1)

四、总结

选择排序是一种简单但效率较低的排序算法，适用于数据量较小的场景。它的优点是实现简单，缺点是时间复杂度较高，不适用于大规模数据排序。

如果这篇文章对您有所启发，期待您的点赞关注！