[日常一练] 最小K个数,堆排序

面试题 17.14. 最小K个数 - 力扣（LeetCode） 

 方法一:

既然是找前K个最小的元素,把那就直接建立小根堆,直接出K次堆顶元素即可

 public static int[] smallestK(int[] array, int k) {
        PriorityQueue<Integer> minqueue = new PriorityQueue<>(array.length);
        //把这个数组直接建堆,要找前K个最大的,出K次堆顶元素即可;时间复杂度是n * log2n
        for (int i = 0; i < array.length; i++) {
            minqueue.offer(array[i]);
        }
        //建成最小堆后,出K次
        //出出来的元素放到新的数组中去
        int[] ret = new int[k];
        for (int i = 0; i < ret.length; i++) {
            ret[i] = minqueue.poll();
        }
        return ret;
    }

方法二:

堆排序:

目标:将这组数据从小到大排序!!建立大根堆好>还是建立小根堆合适?

将一组数据从小到大去排序,先建立一个大根堆,然后再去排序

思路:(欢迎指导)

创建一个大根堆,然后把这个堆顶元素(此刻堆顶元素一定是最大的)放到最后一个位置,此刻最后一个元素就有序了,交换完毕之后,继续调整为大根堆,再从调整后最后一个元素-1的位置开始循环调整,最后这个数组就会变成小根堆,从小到大排序完毕,想出K个出K个即可,此题解

代码:

    //堆排序
    public void heapSort() {
        int end = usedSize - 1;
        //堆排序,和数组的最后一个交换,然后进行下一个的交换
        while(end > 0) {
            swap(elem,0,end);
            //先交换,然后循环交换下一个,直到变为小根堆
            shiftDown(0,end);
            end--;
        }
    }
}




  /**
     * 交换方法;
     */
    public void swap(int[] array,int i ,int j ) {
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }



/**
     *向下调整;
     * @param root 是每棵子树的根节点的下标
     * @param len  是每棵子树调整结束的结束条件
     * 向下调整的时间复杂度：O(logn)
     */
    private void shiftDown(int root,int len) {
        //此刻拿到父亲节点的值和数组的长度之后,就要找孩子节点的下标去比较并且交换,完毕即可;
        int child = 2 * root + 1;
        while(child < len) {
            //孩子节点必须小于数组的长度才能进来
            //能进来就代表最少有一个左节点
            if(child + 1 < len && elem[child + 1] > elem [child]) {
                //右孩子节点下标 小于 有效数组长度,并且 右孩子 比 左孩子 大
                child++;
                //代码走到这 就说明 已经 找到 根节点下左右孩子最大值的下标了 并且这个下标是右孩子;
                //如果没进来说明 两种 情况 ,一种是  没有右孩子, 或者 右孩子 没有 左孩子大;
            }
            //你找到最大值之后要干嘛? , 当然是和根 节点的值相比较,如果大与就交换即可;
            if(elem[root] < elem[child]){
                int tmp = elem[root];
                elem[root] = elem[child];
                elem[child] = tmp;
                root = child;
                child = 2 * root + 1;
            } else {
                break;
            }

        }
    }

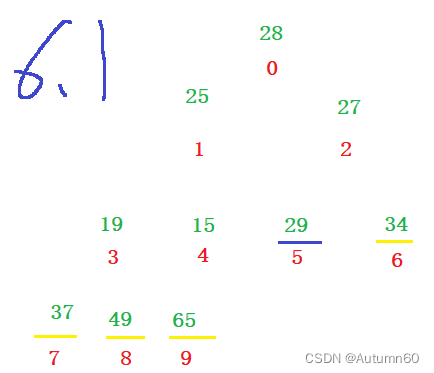
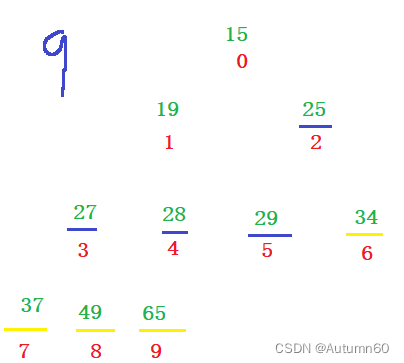
原数组加图解:

这里横线代表一个数调整完毕