二叉树的介绍及其堆的实现

原创 于 2022-11-04 16:30:16 发布
· 286 阅读 · 0 ·
版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#numpy #c++

 

一、二叉树的介绍

1.树的主要特点：

                        1.树是非线性的数据结构。

                        2.任何树都会被分成根和子树。

                        3.树是递归的定义。

                        4.有一个特殊节点，称为根节点。

                        5.树形结构中，子树之间不能有交集，否则就不是树形结构。

                        6.除了根节点外，每个节点有且仅有一个父节点。

                        7.一棵树N个节点的树有N-1条边。

                

2.树的相关概念：

节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6

叶节点或终端节点 ：度为 0 的节点称为叶节点； 如上图： B 、 C 、 H 、 I... 等节点为叶节点
非终端节点或分支节点 ：度不为 0 的节点； 如上图： D 、 E 、 F 、 G... 等节点为分支节点
双亲节点或父节点 ：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图： A 是 B 的父节点
孩子节点或子节点 ：一个节点含有的子树的根节点称为该节点的子节点； 如上图： B 是 A 的孩子节点
兄弟节点 ：具有相同父节点的节点互称为兄弟节点； 如上图： B 、 C 是兄弟节点
树的度 ：一棵树中，最大的节点的度称为树的度； 如上图：树的度为 6
节点的层次 ：从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推
树的高度或深度 ：树中节点的最大层次； 如上图：树的高度为 4
堂兄弟节点 ：双亲在同一层的节点互为堂兄弟；如上图： H 、 I 互为兄弟节点
节点的祖先 ：从根到该节点所经分支上的所有节点；如上图： A 是所有节点的祖先
子孙 ：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是 A 的子孙
森林 ：由 m （ m>0 ）棵互不相交的树的集合称为森林

3.二叉树类型的介绍：

满二叉树：一个二叉树，如果每一层的节点数(h每层节点数2^(h-1),h为层数)都达到最大值，则这个二叉树就是满二叉树。如果一个二叉树的层数为K，且节点总数是(2^k)-1 (k为总层数),则它就是满二叉树。

有以下特点：1.所有叶子节点都在最后一层

2.所有的分节点都有两个孩子

当然还有完全二叉树：

1.前k -1层都是慢的（k为总层数）

2.最后一层不满，但是最后一层从左到右是连续的。

3.满二叉树可以说是一颗特殊的完全二叉树

 4.二叉树的性质

二叉树有以下几个性质：TODO(上标和下标)
性质1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2：深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

性质5：

假设partent是父亲节点在数组中的下标：leftchild=partent*2+1 ,  rightchild=partent*2+2。

假设孩子的下标是child，不管左孩子还是右孩子，partent=(child-1)/2。

5.二叉树的存储结构

二叉树有两种存储结构一是顺序存储，所谓顺序存储就是使用数组

还有一种链式的结构

 

 这一个是物理结构一个是逻辑结构


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;//左孩子
	struct BinaryTreeNode* right;//右孩子
	BTDataType data;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	assert(node);

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

二、叉树的顺序结构实现

2.1 二叉树的顺序存储

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

2.2 堆的概念及其结构

大堆（大根堆）：树中一个树及子树中，父亲都大于等于孩子。

小堆（小根堆）：树中一个树及子树中，父亲都小于等于孩子。

 

2.3 堆的实现（ 建大堆）

堆的主要难点其实就是向上调整算法

和向下调整算法

这是堆的声明

#pragma once
#include<iostream>
#include<stdio.h>
#include<stdio.h>
#include<string.h>
#include<assert.h>


using namespace std;



typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capcaity;

}HP;
void HeapInit(HP* hp);//初始化
void HeapDestroy(HP* hp);
void HeapPush(HP* hp,HPDataType x);//插入
void HeapPop(HP* hp);//删除
bool HeapEmpty(HP* hp);//判空
int HeapSize(HP* php);//大小
void AdjustUp(HPDataType* a, int child);//向上调整
void AdjustDwon(HPDataType* a, int size, int parent);//向下调整算法
void HeapPrint(HP* hp);//打印

这是堆的实现

#include"Heap.h"

void HeapInit(HP* hp)
{
	assert(hp);
	hp->a = nullptr;
	hp->capcaity = hp->size = NULL;
	
}
void HeapDestroy(HP* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capcaity = hp->size = 0;
}
void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void HeapPush(HP* hp,HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capcaity)
	{
		int newcapicaty = hp->capcaity == 0 ? 4 : hp->capcaity * 2;//如果他为0扩容2倍
		HPDataType*tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType)*newcapicaty);
		if (tmp == NULL)
		{
			printf("扩容失败");
			exit(-1);
		}
		hp->a = tmp;//指向新空间
		hp->capcaity = newcapicaty;
	}

	hp->a[hp->size] = x;//数组的覆盖删除因为size是数组最后一个位置
	hp->size++;

	AdjustUp(hp->a, hp->size - 1);
}
void HeapPrint(HP* hp)
{
	assert(hp);
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;//公式的出父亲=孩子-1处于2
	while (child > 0)
	{
		if (a[child] < a[parent])//小堆孩子比父亲小就往上进行调整
		{
			Swap(&a[child], &a[parent]);
			child = parent;//把父亲的位置给孩子继续往上走
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(HP*hp)
{
	assert(hp);
	assert(hp->size > 0);//堆区必须有元素
	//这里思路是吧堆顶的数据和最后一个元素进行交换在向下调整
	Swap(&(hp->a[0]), &(hp->a[hp->size - 1]));
	hp->size--;

	AdjustDwon(hp->a, hp->size, 0);
}
void AdjustDwon(HPDataType* a, int size, int parent)//向下调整算法
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		//1.选出左右节点晓得那个
		if (child + 1 < size && a[child + 1] > a[child])//右节点<左节点 
			//child+1防止右边没节点
		{
			child++;
		}
		//小的孩子进行比较
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

堆的测试

#include"Heap.h"
#include<time.h>
void TestHeap()
{
	HP hp;
	HeapInit(&hp);
	int a[] = { 10,15,19,25,18,34,65,49,27,37,28};
	for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
	{
		HeapPush(&hp, a[i]);
	}
	HeapPrint(&hp);

}
void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int* kMinHeap = (int*)malloc(sizeof(int)*k);
	assert(kMinHeap);
	for (int i = 0; i < k; ++i)
	{
		kMinHeap[i] = a[i];//把数组所有的元素给这个数组
	}
	for (int i = (k - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDwon(kMinHeap, k, i);//向下调整成为堆
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (int j = k; j < n; ++j)
	{
		if (a[j] > kMinHeap[0])
		{
			kMinHeap[0] = a[j];
			AdjustDwon(kMinHeap, k, 0);
		}
	}

	for (int i = 0; i < k; ++i)
	{
		printf("%d ", kMinHeap[i]);
	}
	printf("\n");
}
void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int)*n);
	srand(time(0));
	for (int i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[120] = 1000000 + 5;
	a[99] = 1000000 + 6;
	a[0] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;
	PrintTopK(a, n, 10);
}

int main()
{
	/*TestHeap();*/


	//TestTopk();


	system("pause");
	

	return 0;
}

2.4 堆向上调整算法

 

 主要调整的是红色的位置

2.5 向下调整算法

注意：while的条件一定是child>0,若是partent >= 0,是不对的。因为：当 partent=0 时 ，child=partent,则 child 的值就是0，partent=(0-1)/2=0。这时这时的 partent==child ,还会重新进入循环，或者进入死循环。

 

 

void AdjustDwon(HPDataType* a, int size, int parent)//向下调整算法
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		//1.选出左右节点晓得那个
		if (child + 1 < size && a[child + 1] > a[child])//右节点<左节点 
			//child+1防止右边没节点
		{
			child++;
		}
		//小的孩子进行比较
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

2.6 堆的插入

HeapPush 需要用到顺序表和向上挑战的知识

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* temp = (HPDataType*)realloc(hp->a, newcapacity *sizeof(HPDataType));
		if (temp == NULL)
		{
			printf("增容失败\n");
			exit(-1);
		}
		hp->capacity = newcapacity;
		hp->a = temp;
	}
		hp->a[hp->size] = x;
		hp->size++;
		AdjustUp(hp->a,hp->size-1);
}

2.7 删除堆顶的数据

删除堆是删除堆顶的数据，将堆顶的数据跟最后一个数据交换，然后删除数组最后一个数据。意义：取最小值或最大值，次小值或次大值依次类推。


void HeapPop(HP*hp)
{
	assert(hp);
	assert(hp->size > 0);//堆区必须有元素
	//这里思路是吧堆顶的数据和最后一个元素进行交换在向下调整
	Swap(&(hp->a[0]), &(hp->a[hp->size - 1]));
	hp->size--;

	AdjustDwon(hp->a, hp->size, 0);
}

2.8 堆的应用

堆主要有两个问题，一个用于TOP k问题 还有一个堆排序问题

TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

1.用数据集合中前K个元素来建堆 (建前K个数的堆，复杂度为O(K))

        前K个最大的元素，建小堆。

        前K个最小的元素，建大堆。

2.用剩余的N-K个元素依次与堆顶数据比较，满足条件则替换堆顶元素，并向下调整。(按照最坏打算，假设每个数都进行交换并向下调整一遍，所以执行了(N-K)*logK次  ）。

3.建堆复杂度是O(N)后面会证，所以TOP-K的复杂度为：O(K+(N-K)*logK)  K很小所以约等于O(N*logK)约等于O(N)。

TOP-K的实现过程：

注意：找前K个最大的数，需要建立小堆。若是建了大堆，堆顶数据最大，如果说这个数据是数组中最大的数，其他次级大的数直接就不可能入堆，会出错。

 

堆排序：

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1.建堆

        升序：建大堆。

        降序：建小堆。

2.利用堆删除思想来进行排序

实现升序，建大堆，分别使用向上调整和向下调整，然后利用堆删除的思想，使数组为升序：

注意：向下调整算法前提是左右子树都是小堆或大堆，一般排序的数组是乱序，按照堆定义根本不符合堆的定义，所以需要向下调整从数组后面的非叶子节点开始调整。

使用向下调整进行建大堆：
 

//需要从数组后面的非叶子节点开始调堆
	int i = 0;
	for (i = (n-1-1)/2; i >= 0; i--)//注意n-1是数组下标在-1是算父亲节点
	{
		
		AdjustDown(a,n, i);
	}

使用向上调整进行建大堆：

	for (int i = 1; i < n; i++)
	{
		AdjustUp(a,i);//用向上调整，建堆复杂度是O（N*logN）
	}

利用堆删除的思想：

	for (int end = n - 1; end > 0; end--)
	{
		Swap(&a[0], &a[end]);//第一个数据与最后一个数据相换
		AdjustDown(a,end,0);//在向下调整
	}

二. 二叉树的实现

1.因为普通二叉树增删改查没有意义所以我创建了一颗简单二叉树

#include <stdio.h>
#include <stdlib.h>
 
typedef char BTDataType;
 
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType Data;
}BTNode;
 
BTNode* ButBTNode(BTDataType x);//创建节点
BTNode* CreatBinaryTree();//创建二叉树
BTNode* ButBTNode(BTDataType x)
{
	BTNode* BTNewNode = (BTNode*)malloc(sizeof(BTNode));
	if (BTNewNode == NULL)
	{
		printf("申请失败\n");
		exit(-1);
	}
	BTNewNode->Data = x;
	BTNewNode->left = NULL;
	BTNewNode->right = NULL;
	return BTNewNode;
}
 
 
BTNode* CreatBinaryTree()
{
	BTNode* node1 = ButBTNode('A');
	BTNode* node2 = ButBTNode('B');
	BTNode* node3 = ButBTNode('C');
	BTNode* node4 = ButBTNode('D');
	BTNode* node5 = ButBTNode('E');
	BTNode* node6 = ButBTNode('F');
	node1->left = node2;
	node1->right = node3;
 
	node2->left = node4;
 
	node3->left = node5;
	node3->right = node6;
	return node1;
}

2.2 二叉树的遍历

前序：根 左子树 右子树

中序：左子树 根 右子树

后续：左子树 右子树 跟

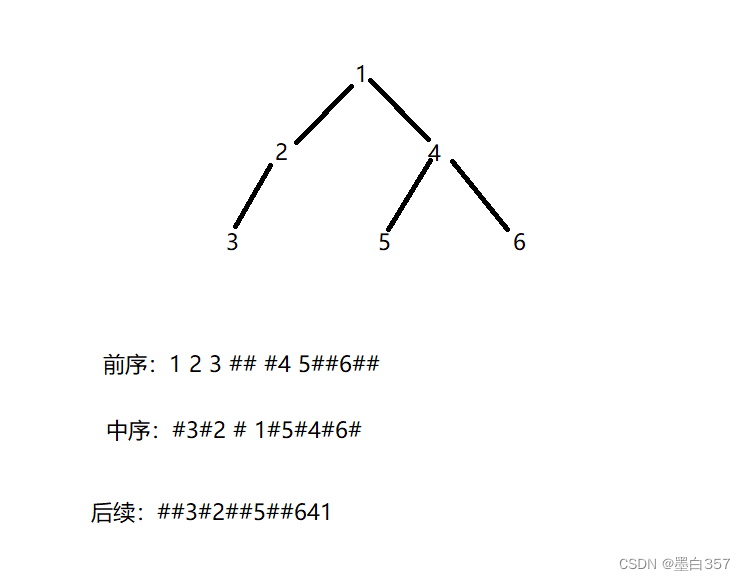
2.3 前序遍历代码实现 

 

//前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
		
	printf("%c ",root->Data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}
//中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	
	BinaryTreeInOrder(root->left);
	printf("%c ", root->Data);
	BinaryTreeInOrder(root->right);
}
//后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->Data);
}

2.4 节点个数以及高度

二叉树节点个数代码实现：

左边+右边+自身

//计算节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

2.5 二叉树叶子节点代码实现

//计算叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

2.6 二叉树第k层节点的个数

//计算第K层的节点
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
	{
		return 1;//只有一层自己就是
	}
	return BinaryTreeLevelKSize(root->left,k-1)+ BinaryTreeLevelKSize(root->right, k - 1);
     //每一层往下走k-1层 比如说k=3 第二层就走2层
}

2.7 二叉树查找

//找值为X的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->Data == x)
		return root;
	BTNode* LeftNode = BinaryTreeFind(root->left, x);
	if (LeftNode != NULL)
		return LeftNode;
	BTNode* RightNode = BinaryTreeFind(root->right, x);
	if (RightNode != NULL)
		return RightNode;
	return NULL;
}

2.8 二叉树的深度

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
		return 0;
 
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);
	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

墨白1357

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值