Day13 Error surface is rugged……
Tips for training :Adaptive Learning Rate
critical point is not the difficult





Root mean Square --used in Adagrad

这里为啥是前面的g的和而不是直接只除以当前呢?
这种方法的目的是防止学习率在训练过程中快速衰减。如果只用当前的梯度值来更新学习率,那么任何较大的梯度值都可能会导致很大的学习率变化,这可能会使得学习过程不稳定。通过使用所有过去梯度的平方的平均值,我们可以使学习率的变化更加平滑,因为这个值不会因为个别极端的梯度值而发生剧烈波动。
以及这个式子和之前讲的那个正则化是不是一样的呢?
啊!!!woc 我发现这两个是差不多的思想啊,你把上面那个正则化的东西用Gradient做出来
gi = 2xw+ ∑ \sum ∑ 2w…… 额……好吧完全不一样,但是我又不知道这个会不会对于我的……废了,乱了;稳一稳哈
- 这里为什么不是让这个梯度直接等于0 呢?-- 或许是因为有的loss function 我们无法直接求出来梯度等于0 的w?哦哦 那我就知道了md 吓死,差点以为自己的machine Learning route ending了


RMSProp
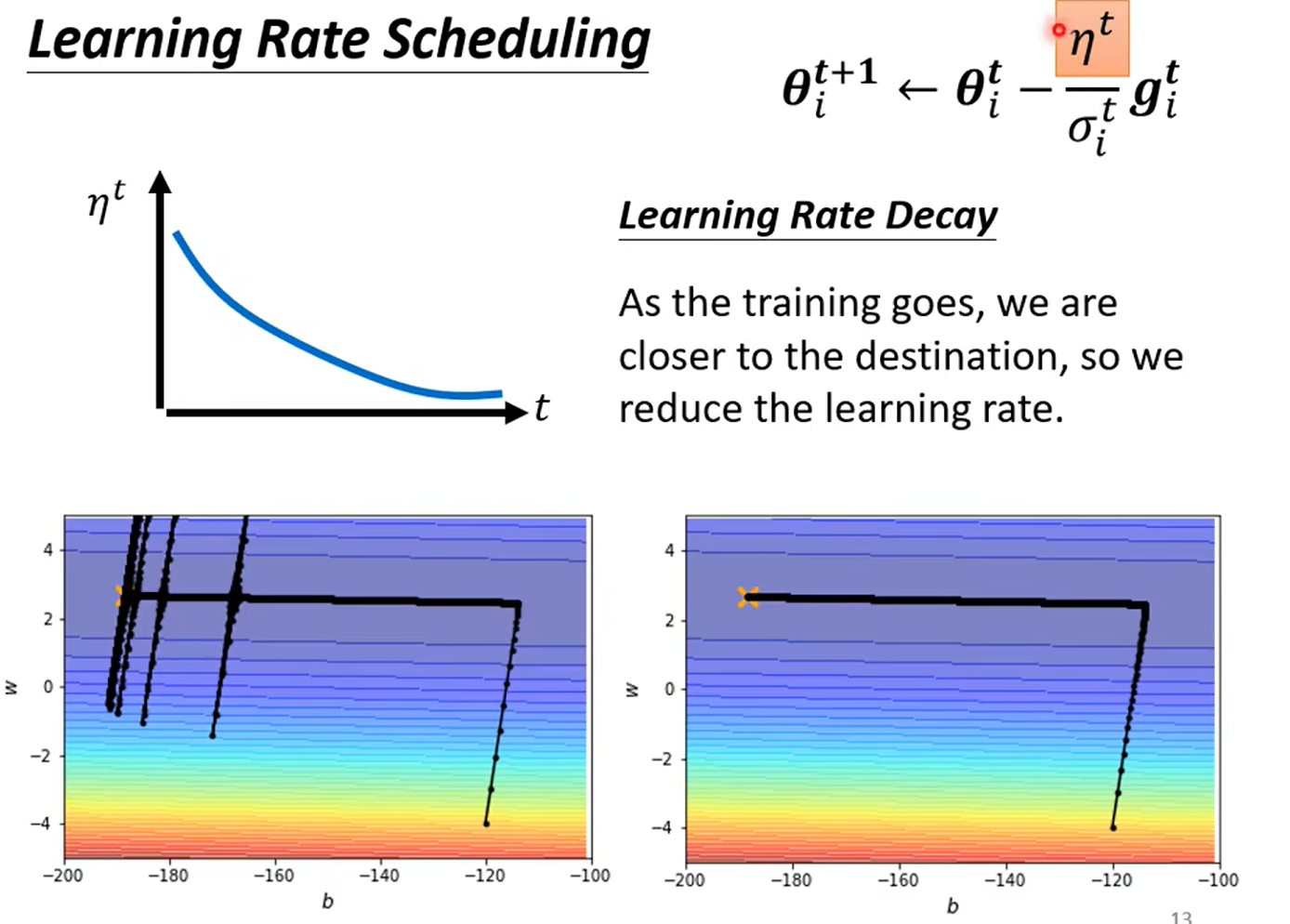
因为上一个方法只能解决 不同的 θ \theta θ 时候的学习率,但是由图我们可以知道有时候同一个参数我们也希望起有变化率的不同取值

我怎么没看出来这种思想啊


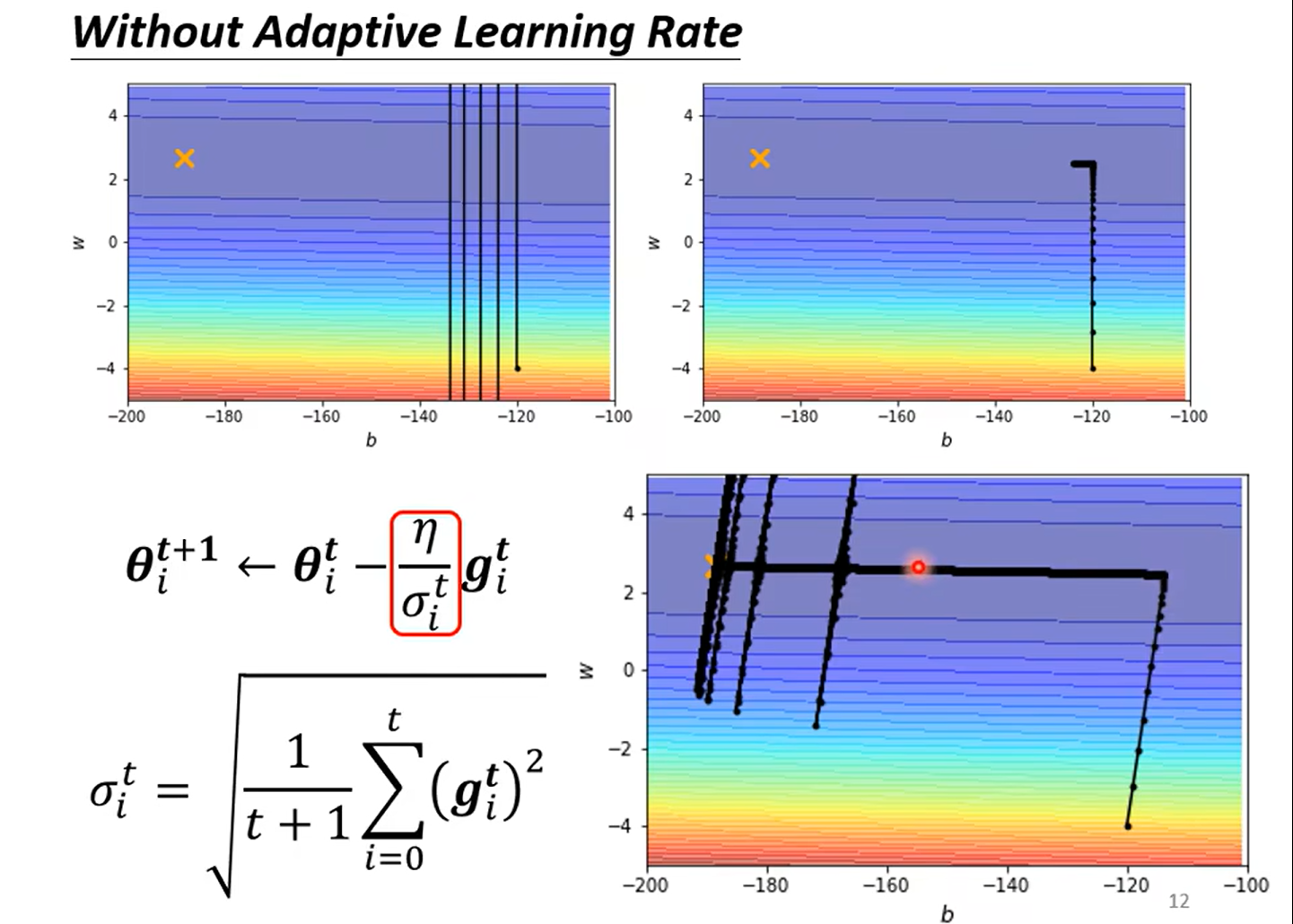

解决井喷问题

在bert里面需要用到


SUmmary of OPtimization


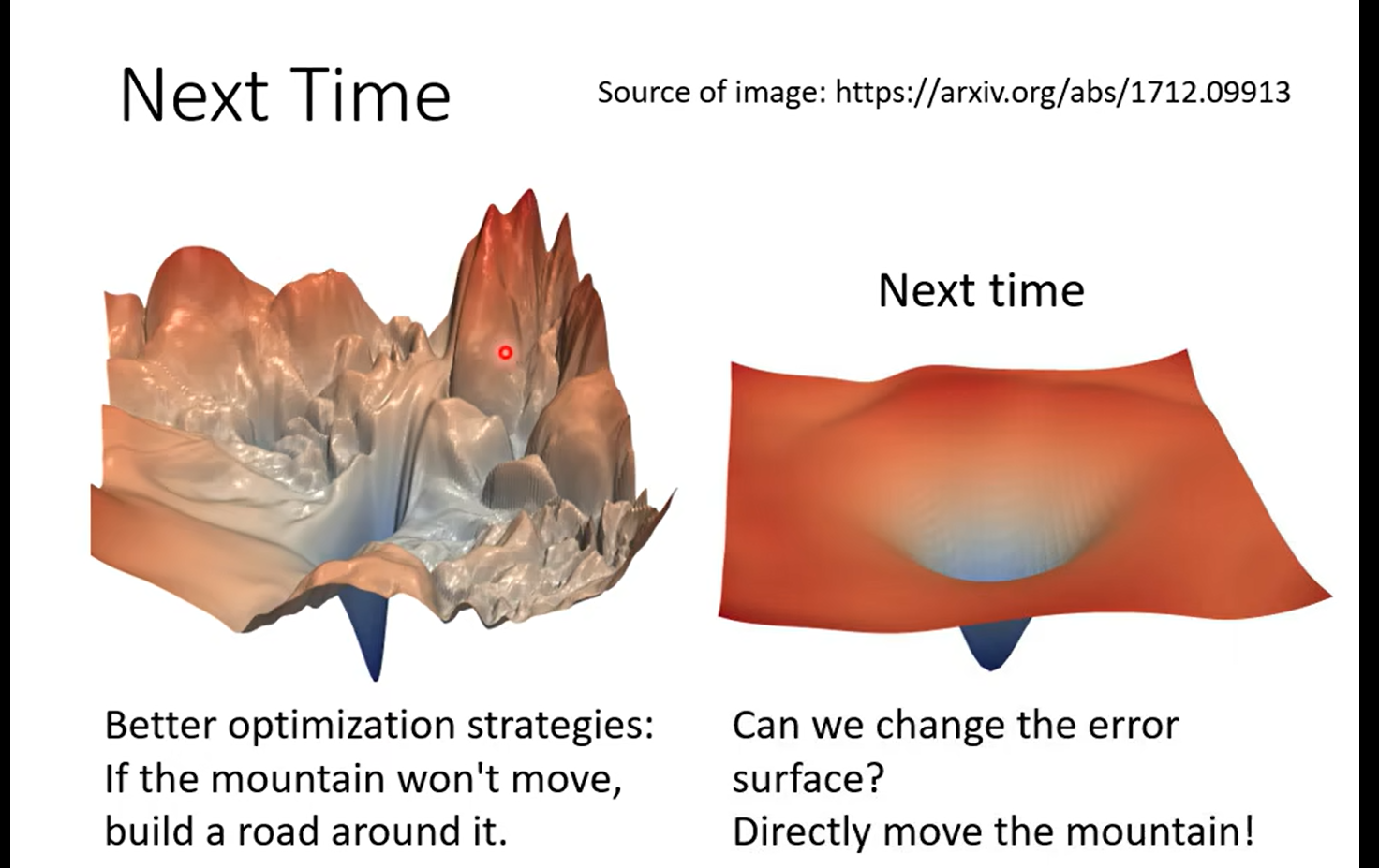
下节预告:


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








