树、树、树

树：

目前学过的基本数据结构

1.数组 链表 哈希表

哈希表本身是数组加链表   达到O(1)

不管存储什么数字，根据数除以数组长度的余数

考虑一个链表，是O(n),短的话是O(1)

能不能降低时间复杂度

循环减半logn —— > 折半查找

有一个有序数组

进行查询可以用一个折半查找法

 找到中间位置：首尾相加/2

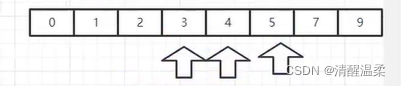
数组必须有序才能达到logn

链表是可以达到logn时间复杂度

树也是链式存储，特殊的树可以达到logn

先学一个，有序二叉树

树的根节点必须大于等于左子树

必须小于等于右子树

 画一个特殊的树

每次查询折掉一半的数据，O(1)

树的存取和读取效率比较高。

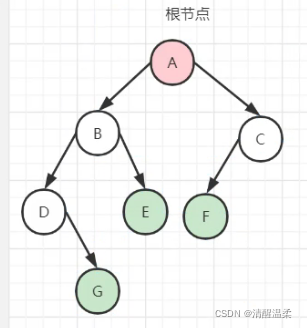
树的概念：

（树可能有很多叉）

1.节点 根节点 父节点 子节点 叶子结点

2.节点的权（节点的值）

3.路径：（从根节点到该节点走过的节点）

4.层

5.子树

例如：画圈的

6.树的高度：有几层

7.森林：多颗子树构成森林

二叉树：每个节点上最多有两个节点称为二叉树。

满二叉树：最后一层的数据也是铺满的。

完全二叉树：从上到下从左到右依次进行平铺。

===================================================

二叉树的遍历说明

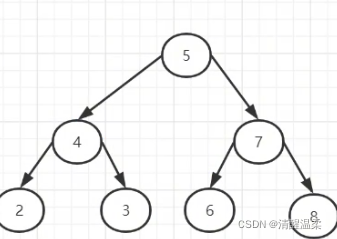
• • 深度优先遍历：

• • 先序遍历：先输出父节点，再遍历输出左子树，再遍历输出右子树

• • • 中序遍历 ：先左再父再右

• • • 后序遍历 2 3 4  6 8 7 5

• • 广度优先遍历
    • 层次遍历 一层一层遍历