ps:动态规划常见题型
文章目录
动态规划常见问题
大家劫舍
挺简单的,但是没做出来。当时想成背包问题了,然后没搞明白 99 1 2 88这种情况怎么处理
如 6 99 1 2 99 6,这种情况。最优选取是99 ,99。
自己模拟一下,就知道了 – 一定要理清楚,这点(99,99可以由下面的递推公式推出来)挺重要的
然后也没有容量问题,所以很难抽象成背包吧
仔细一想,当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。 – 本质就是当前房屋偷不偷,然后得出推导公式
所以这里就更感觉到,当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。


dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历!
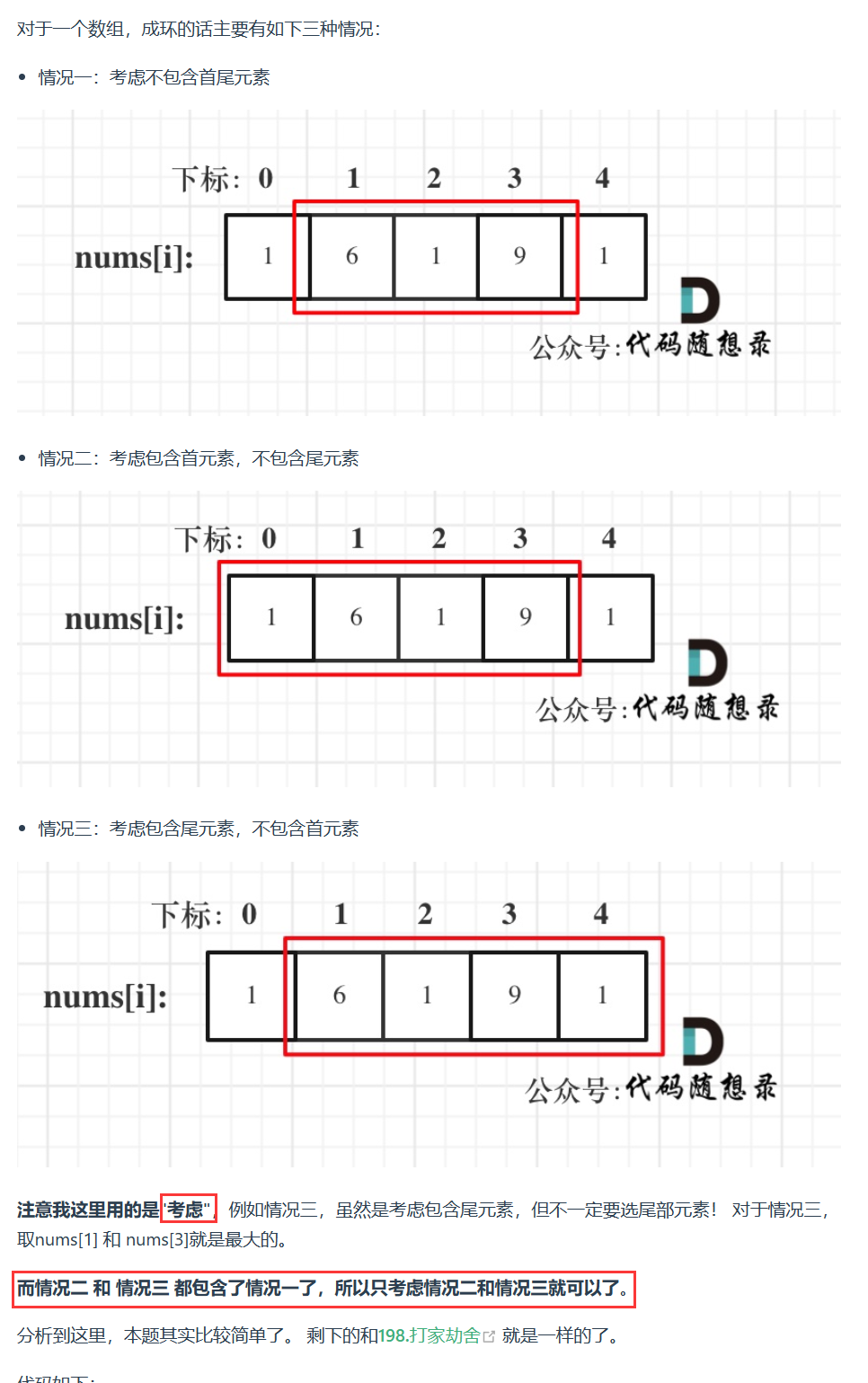
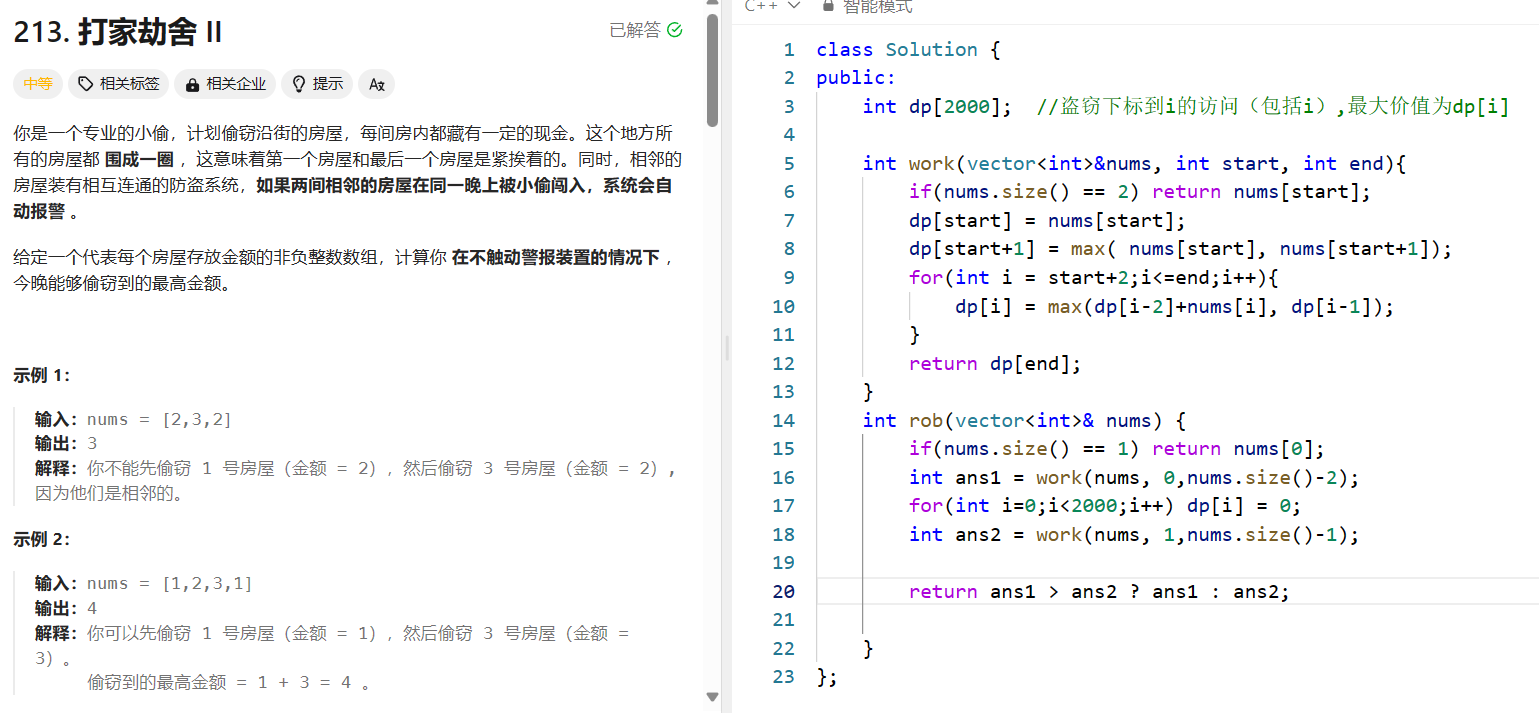
打家劫舍II
环形问题,最后答案的选取有三种情况
买卖股票的最佳时机
贪心:

动态规划:



买卖股票的最佳时机II
可以无限次买卖 – 和III IV的区别
动态规划解法:
和上一题很类似,就是多了可以多次购买股票(但是任意时刻最多持有一股)



dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。
上面两题的结果其实就是dp[len-1][1] – 卖出股票后的钱肯定 大与 买入股票后的钱
买卖股票的最佳时机III
分为5个状态(可以省略一个),注意理解持有的意思

买卖股票的最佳时机IV
困难题a出来啦哈哈哈
其实就是上一道的延伸,做上一道的时候我还在想,万一最多可以交易三次咋办。看到这道题我就狂喜哈哈哈
使用二维数组 dp[i][j] :第i天的状态为j,所剩下的最大现金是dp[i][j]
j的状态表示为:
- 0 表示不操作
- 1 第一次持有股票
- 2 第一次卖出
- 3 第二次持有股票
- 4 第二次卖出
**找规律 ** 除了0以外,偶数就是卖出,奇数就是买入。
j == 1 其实也可以不用写可以合并进else里面

买股票的最佳时机含冷冻期
也是a了出来,比老师的方法简单
类似与打家劫舍的方法

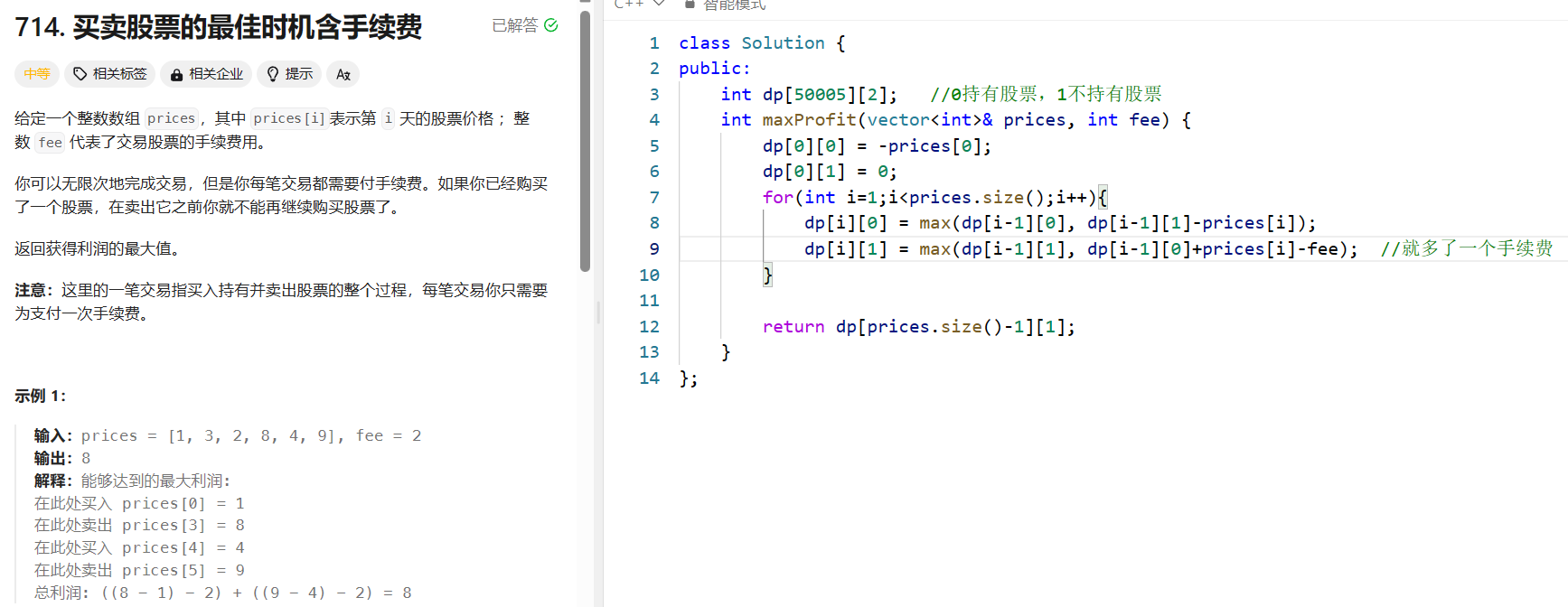
买股票的最佳时机含手续费
Leetcode股票问题总结篇!

121 122都可以用贪心做,很简单。 但是练手的时候还是用动态规划好一点,更系统
121 122 309 714 都只有两种状态
dp数组定义:
- dp[i][0] 表示第i天持有股票所得现金
- dp[i][1] 表示第i天不持有股票所得最多现金
122 123 有2*k种状态 – 然后也是有规律的,相邻两天之间是有规律的
- 第一次买入
- 第一次卖出
- 第二次买入
- 第二次卖出
- …
最长递增子序列
第一次接触子序列相关的题目,dp[]的定义还是挺巧的
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i] 和 题解里面的dp的意思一样

最长连续递增序列
暴力:

动态规划:
和上一题很类似,区别就是连续

子序列默认不连续,子数组默认连续
最长重复子数组
第一次看还是挺懵逼的,但是本质不难
dp数组的定义也很讲究,i-1,j-1可以减少初始化的工作量
本题的细节
- dp的定义问题
- for循环的遍历 【1,size】;
- 不相等情况默认 就是默认值0了

最长公共子序列
要处理相等,不相等时(继承哈哈哈)
不相等时:
如
abc
ace
c 和 e已经不相等了,就没有必要在比较了。我们就可以回退dp(和现在不回退是等价的),然后回退有两种方式


不想交的线
和上一题一样

最大子数组和
贪心:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ans = -2000000000, sum = 0;
for(int i=0 ;i<nums.size(); i++){
sum += nums[i];
ans = ans > sum ? ans : sum;
if(sum < 0) sum = 0; //前面的总和为负时,直接全部放弃 重新累计
}
return ans;
}
};

判断子序列
我直接把它抽象成求两个子串的重复子序列了
dp定义中应该为最长公共子序列的长度为dp[i] [j]

编辑距离本质就是删除字符串里面的字母
dp[i][j] = max(dp[i-1][j], dp[i][j-1]); 我上面的题解是不相等时可以删两个字符串(即两种删法)
其实本题不相等时只需要删一个字符串就行了
编辑距离的解法(也是dp):
class Solution {
public:
bool isSubsequence(string s, string t) {
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1]; //s不删,只删t
}
}
if (dp[s.size()][t.size()] == s.size()) return true;
return false;
}
};

接龙数列

当时第一反应就是DP,然后信心满满(都DP了是吧),感觉可以拿满分
但是交卷后发现才拿了一半的分,然后看了眼数据范围 1e5 ,我感觉要是1e4应该就全过了
#include <bits/stdc++.h>
using namespace std;
long long dp[100005],n,arr[100005],len ;
int sta(int x){
while(x >= 10){
x /= 10;
}
return x;
}
int en(int x){
return x % 10;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
dp[i] = 1;
}
if(n == 1){
cout<<0;
return 0;
}
for(int i=2;i<=n;i++){
for(int j=1;j<i;j++){
if(sta(arr[i]) == en(arr[j])){
dp[i] = max(dp[i], dp[j]+1);
}
len = max(len, dp[i]);
}
}
cout<<n-len;
return 0;
}
然后看了题解,神仙做法 真的很厉害 直接不需要内层循环了
#include <bits/stdc++.h>
using namespace std;
long long dp[100005],n,arr[100005],len; //dp 以arr[i]为结尾的接龙数组,最大的长度为dp[i]
long long val[20]; //以数值i为结尾(i的数值为0到9)的接龙数列,最大的长度为val[i]
int sta(int x){
while(x >= 10){
x /= 10;
}
return x;
}
int en(int x){
return x % 10;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
dp[i] = 1;
}
if(n == 1){
cout<<0;
return 0;
}
for(int i=1;i<=n;i++){
dp[i] = val[sta(arr[i])] + 1; //不需要遍历直接定位到对应的最大值
val[en(arr[i])] = max(val[en(arr[i])], dp[i]); //更新对应的数据
len = max(len, dp[i]); //记录答案
}
cout<<n-len;
return 0;
}
不同的子序列
- dp数组定义
- 递推公式还是挺有讲究的

递推公式得慢慢理解,多看
- 简单理解就是也不用s[i-1]

两个字符串的删除操作
直接秒了

解法二:

由上面两种解法我们可以发现,dp数组的定义是很重要的。dp数组的定义不同,递推公式就不同,初始化也就不同
编辑距离
一开始不知道插入该怎么操作会不会涉及word字符串长度变换啥的 – 导致for循环条件变化.
后面发现想多了,之前删了那么多次,也没见for循环条件改变啥的。 然后就是插入可以理解为删除,他们是等效的。
- 注意初始化


编辑距离总结
注意dp的定义



子序列问题 + 编辑距离总结
绝大部分是求长度大小,小部分求个数
所以是一个数值
dp数组一般是怎么定义的?
一般就两种定义方法
- 以下标i-1结尾的s1,和 以下标j-1为结尾的s2 的最小公共子序列/子数组 的长度为 dp[i] [j] – 两个数组时
- 以nums[i]为结尾的子数组/子序列
都是由什么推过来的
在给两个数组的子序列里面,dp[i] [j] 的推导公式一般只与 dp[i-1] [j], dp[i] [j-1], dp[i-1] [j-1] 有关!
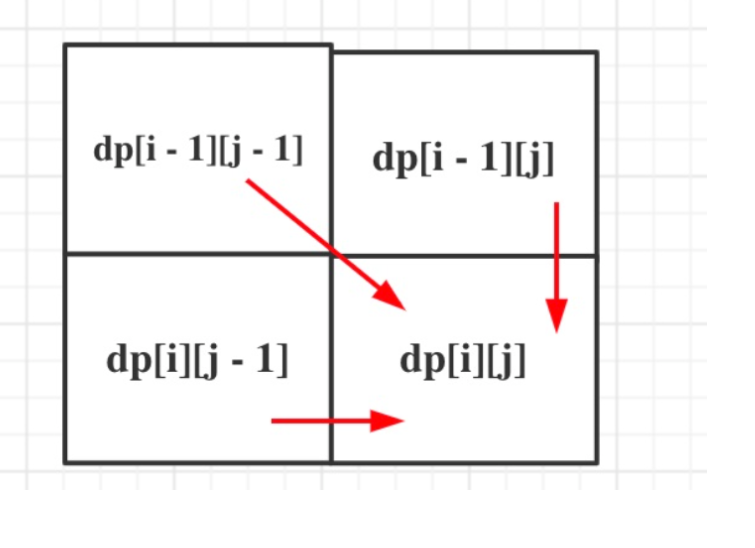
关于玄学dp
实在不行可以试试玄学dp(遇见新的不会的题时,最后实在没办法)。 dp[i-1] [j], dp[i] [j-1], dp[i-1] [j-1]直接怼上去试试
回文子串
双指针法:
关键就是找中心,然后向两边扩
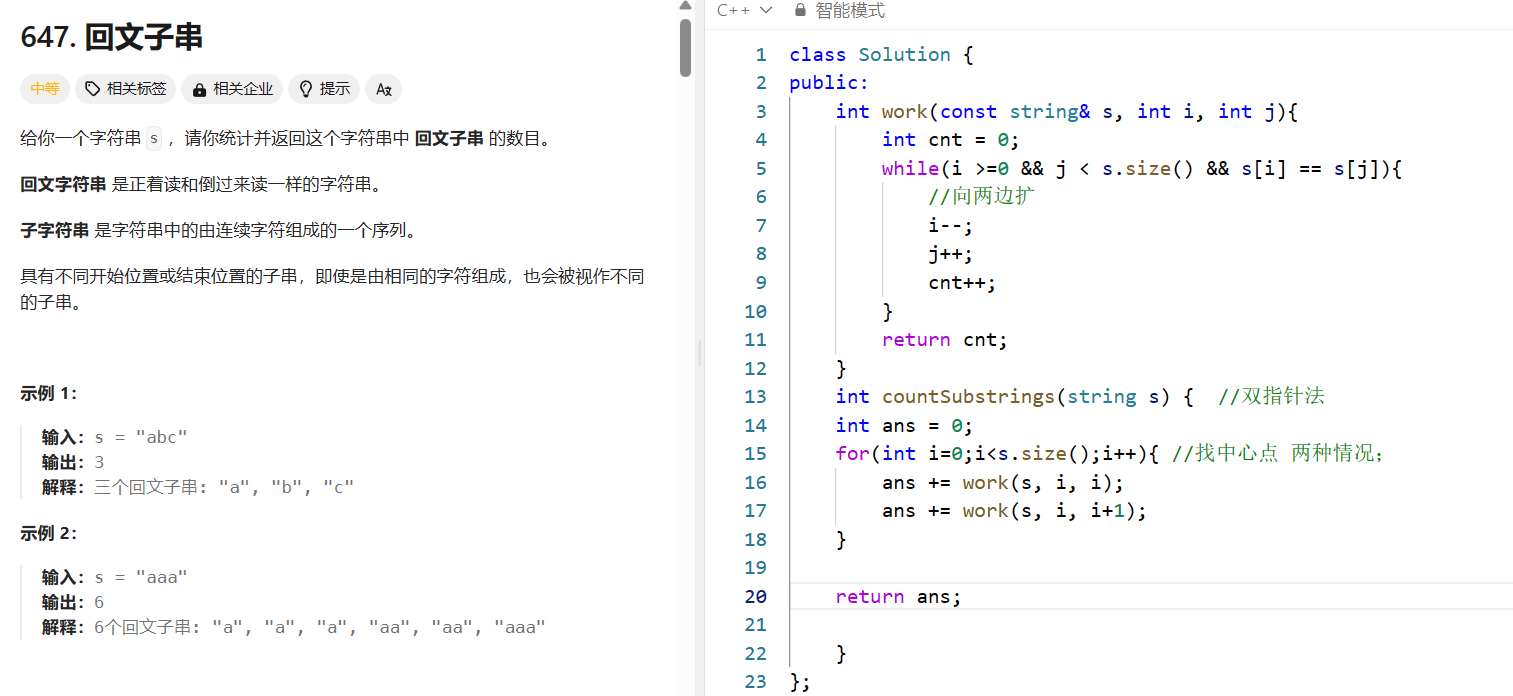
动态规划:

容易掉进思维定式 – dp数组的含义


递推公式

遍历顺序
遍历顺序都是由递推公式决定的!!!


注意因为dp[i] [j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
最长回文子序列
和上一题差不多
所以目前来说可以得到一个规律,关于回文串的dp,通常定义为二维的dp[i] [j],表示范围的
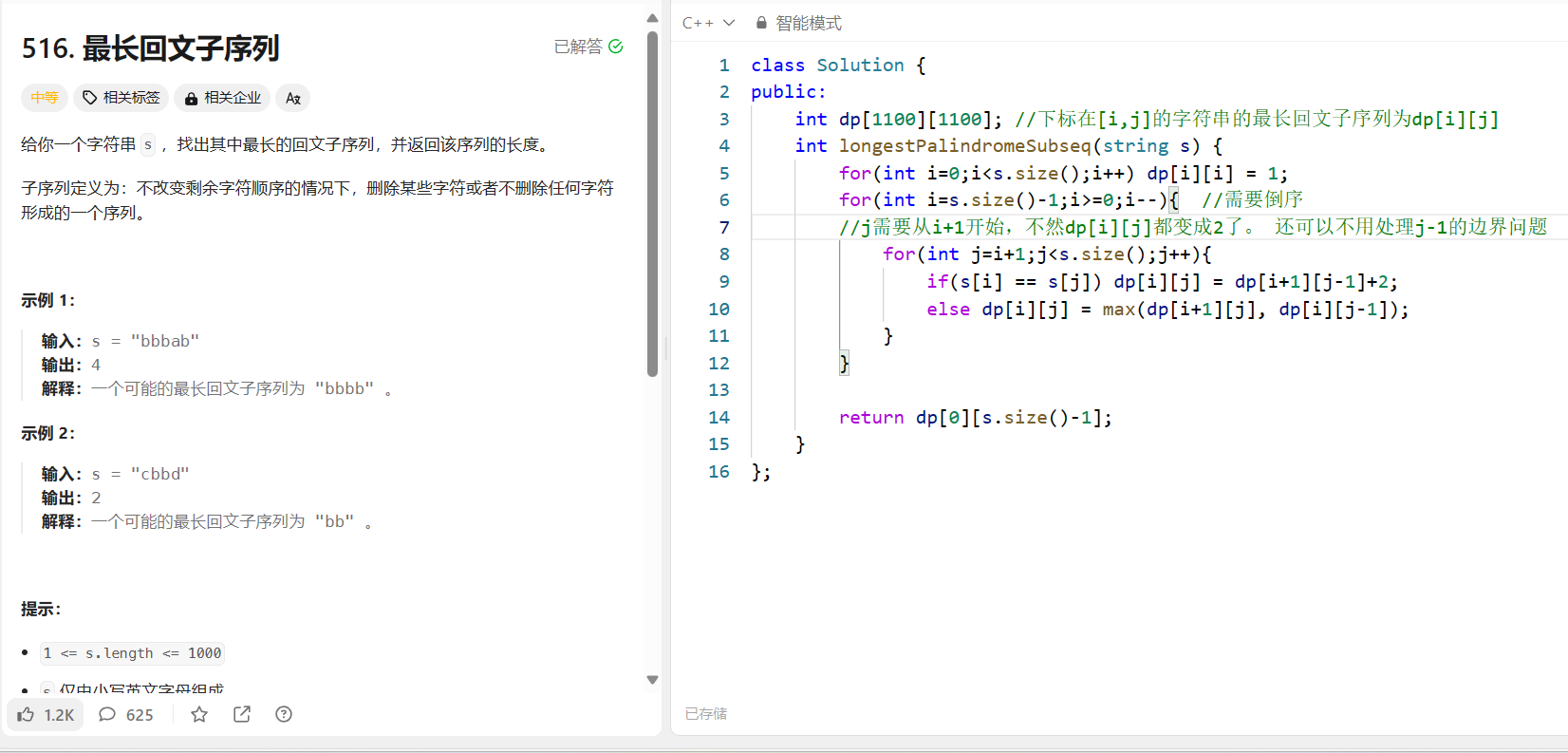
动态规划大总结





此文章用于笔者记录学习,也希望对你有帮助
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








