XJTUSE-图形学

YiYo832

已于 2023-12-01 16:29:45 修改

阅读量2.4k

点赞数 33

分类专栏： XJTUSE-大三上文章标签：软件工程

于 2023-11-25 00:08:03 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_64112516/article/details/134566258

版权

XJTUSE-大三上专栏收录该内容

20 篇文章

订阅专栏

本文是计算机图形学的复习资料，涵盖研究内容、发展历史、图形设备等基础知识，介绍直线段、圆弧扫描算法，多边形扫描转换与填充等，还涉及参数曲线与曲面、颜色视觉、光照明模型等，最后有20届期末考题及答案，以及OpenGL相关知识。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

非常感谢泉佬的笔记，同时感谢祝老师把资源都放出来。（不像某些PPT用7年的老师|_|）

希望看到这篇的同学考试顺利！！！

本文转载部分blog，若侵权，请联系

请注意，编写者为21届考生。

部分内容为略，但不代表一定不涉及考试，各届需根据祝老师的说法适当改变。

2023-11-24 开始复习，主要是最近事情也不少，各种DDL，复习也不连续，写到哪里算哪里吧。

2023-11-30 16:37 更新了部分省略的内容。

前言

复习资料参考：

泉和其他学长学姐的笔记：

计算机图形学_雨落俊泉的博客-优快云博客

老师群里发的笔记：eg:习题2.pdf

最后一节课的视频

思源学堂上的OpenGL相关内容+PPT

下面先进行知识汇总和复习，其实泉佬的很全了，我主要是自己写一下复习，建议同学们看泉的。我自己写的主要是按照PPT上面来着，有些一概而过，有些压根没写

第一章

1.1 研究内容

典型的图形系统由图形输入、图形输出和图形处理系统组成。

图形的要素：

几何要素：刻画对象的轮廓、形状等
非几何要素：刻画对象的颜色、材质等

图形图像表示法：

点阵图
矢量图

1.2 发展历史

个人想法：我觉得发展历史这一块了解啥的就好了，没想到老师真出考题，哎/>_<\。被迫整理笔记

1.2.1 历史追溯

CRT的出现为计算机生成和显示图形提供了可能.

MIT林肯实验室，在Whirlwind上开发SAGE空中防御系统，通过光笔在屏幕上指点与系统交互标志着交互式图形技术的诞生.

Ivan.E.Sutherland的博士论文：Sketchpad：一个人机通信的图形系统。该系统确定了交互图形学作为一个学科分支.

1.2.2 发展历史

图形显示器的发展

图形输入设备的发展

第一阶段：控制开关、穿孔纸等等
第二阶段：键盘
第三阶段：二维定位设备，如鼠标、光笔、图形输入板、触摸屏等等，语音
第四阶段：三维输入设备（如空间球、数据手套、数据衣），用户的手势、表情等等
第五阶段：用户的思维

1.3 图形学应用（略）

1.4 当前研究状况

图形学的杂志和会议

会议：

Siggraph
Eurograph
Asiagraph
IEEE Virtual Reality
IEEE Visualization Conference

杂志

ACM Transaction on Graphics
IEEE Computer Graphics and Application
IEEE Visualization and Computer Graphics
IEEE T. on Visualization and Computer Graphics
Graphical Models
Computer Graphics Forum
The Visual Computer

1.5 图形设备（重点）

显示器：

CRT：技术成熟，亮度和对比度好，有极少量辐射，体积大并且笨重
LCD：要有光源才能显示图像，可以做到数字信号直接显示，失真小，体积小，重量轻
LED：发光效率高，寿命长，一般做LCD的光源

打印机：

针式打印机：依靠打印针击打色带在打印介质上形成色点的组合来实现规定字符和图像（24针）
喷墨打印机：打印头上的喷口将墨滴按特定的方式喷到打印介质上形成文字或图像, 分为热汽泡式和压电式
激光打印机：采用电子成像技术，激光束扫描感光鼓，将墨粉吸附到感光区域，再将墨粉转印到打印介质上，最后通过加热装置将墨粉熔化固定到打印介质

1.6 相关开发技术（略）

第二章

基本概念

扫描转换（光栅化）：确定最佳逼近图形的像素几何，并用指定属性写像素的过程
区域填充：光栅化过程中确定区域对应的像素集，并用指定的属性或图案显示
裁减：确定一个图形的哪部分在窗口内显示
走样：由于显示器的空间分辨率有限，因像素逼近误差，使所画图形产生畸变（台阶、锯齿）的现象
反走样：减少或消除走样的技术：硬件、软件的方法
隐藏部分：当不透光的物体遮挡了来自某些物体部分的光线，使其无法到达观察者
消隐：把隐藏的部分从图中删除，消除歧义性

直线段扫描算法

建议自己翻书看算法，我不给出详细讲解了。

数值微分法（DDA）
中点画线法
Bresenham算法

数值微分法（DDA）

算法代码：

void DDALine(int x0,int y0,int x1,int y1,int color)     
{     
    int x；							
	float dx, dy, y, k;						
	dx= x1-x0, dy=y1-y0;					   
	k=dy/dx, y=y0;	 					   
	for (x=x0; x<=x1, x++)					   
	{
       drawpixel (x, int(y+0.5), color);		   
	   y=y+k;
     }
}

关键点：y+5

中点画线法

算法代码：

void MidpointLine (int x0, int y0, int x1, int y1, int color) {
	int a, b, d1, d2, d, x, y;
	a = y0 - y1, b = x1 - x0, d = 2 * a + b;
	d1 = 2 * a, d2 = 2 * (a + b);
	x = x0, y = y0;
	drawpixel(x, y, color);
	while (x < x1) {
		if (d < 0)       {
			x++, y++, d += d2;//取右上方
		} else       {
			x++, d += d1;//取右方
		}
		drawpixel (x, y, color);
	}  /* while */
} /* mid PointLine */

关键点：

核心思想为利用中点与直线的距离判断选取哪个点进行绘制
为了减少小数运算，整体*2。

Bresenham算法

算法代码

带有小数计算版本：

void BresenhamLine (int x0, int y0, int x1, int y1, int color) {
	int x, y, dx, dy,i;
	float k, e;
	dx = x1 - x0, dy = y1 - y0, k = dy / dx;
	e = -0.5, x = x0, y = y0;
	for (i = 0; i <= dx; i++) {
		drawpixel (x, y, color);
		x = x + 1，e = e + k;
		if (e >= 0) {
			y++, e = e - 1;
		}
	}
}

消去小数部分计算版本：

void BresenhamLine (int x0, int y0, int x1, int y1, int color) {
	int x, y, dx, dy, i, e;
	dx = x1 - x0, dy = y1 - y0, e = -dx;
	x = x0, y = y0;
	for (i = 0; i <= dx; i++) {
		drawpixel (x, y, color);
		x++, e = e + 2 * dy;
		if (e >= 0)   {
			y++, e = e - 2 * dx;
		}
	}
}

关键点：

核心思想就是利用中点与0.5之间的关系
为了消去小数计算，优化思想如下：

观察 e = e + k; 和 e = e - 1;

其中 e = e + k = e + dy / dx ，为了消去除法

可以转化为 e * dx = e * dx + dy

因为e初始化为-0.5，不妨再乘2得：

2 * e * dx =2 * e * dx + 2 * dy

这时把 e（新） = 2 * e（旧） * dx 后 2 * e * dx =2 * e * dx + 2 * dy 式子就转化为

e = e + 2 * dy

这时候，e（新）初始化应该为 2 * e（旧） * dx = 2 * -0.5 * dx = -dx

现在考虑e = e - 1式子，进行下面转换即可

e * 2 * dx = (e - 1) * 2 * dx

替换后得到：

e（新） = e(新) - 2 * dx

达到了消除小数计算的目的！！！！

（写的有点绕，看不懂的话还请多多包涵！！）

圆弧的扫描转换算法

圆弧扫描算法
角度DDA法
中点画圆法

圆的特征：八对称性。

void CirclePoints(int x, int y, int color) {
	drawpixel(x, y, color);
	drawpixel(y, x, color);
	drawpixel(-x, y, color);
	drawpixel(-y, x, color);
	drawpixel(x, -y, color);
	drawpixel(y, -x, color);
	drawpixel(-x, -y, color);
	drawpixel(-y, -x, color);
}

圆弧扫描算法

简要描述，即利用:Y=±sqrt(R2-X2)直接绘制。

角度DDA法

直接上图（非重点）

中点画圆法

直接上代码：

需要注意的是，代码画的圆是以原点为中心，半径为r的圆！！！

未优化版本（存在小数计算）：

MidPointCircle(int r int color)
{ 
    int x,y;
    float d;
    x=0; y=r; d=1.25-r;
    circlepoints (x,y,color); 
    while(x<=y){
        if(d<0) d+=2*x+3;
        else { 
            d+=2*(x-y)+5; 
            y--;
        }
        x++;
        circlepoints (x,y,color);
    }
}

优化版（不存在小数计算）：

void MidPointCircle(int r, int color) {
	int x, y, d;
	x = 0;
	y = r;
	e = 1 - r;                    // 初值e=1-r
	Circlepoints (x, y, color);         // 画八分对称性的其他点
	while (x <= y) {                        // 画到直线x=y结束
		if (e < 0) e += 2 * x + 3;        // 取右侧点
		else {
			e += 2 * (x - y) + 5;    // 取右下点
			y--;
		}
		x++;
		Circlepoints (x, y, color);       // 画八分对称性的其他点
	}
}

核心思想如下（其实和中点画线一模一样）：

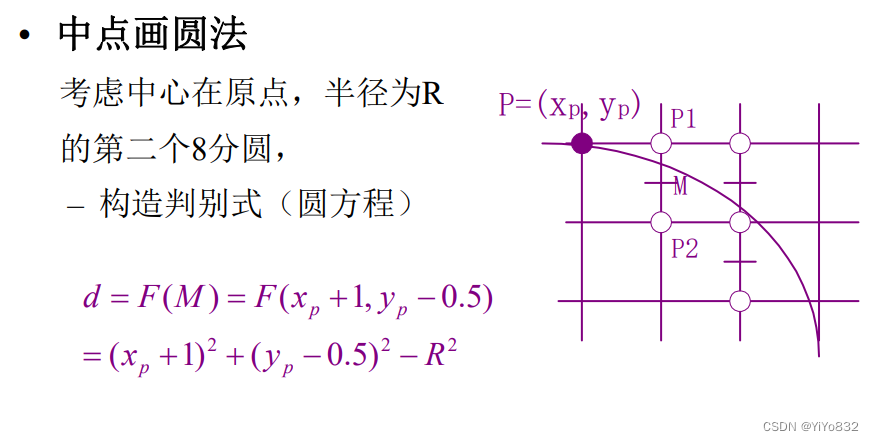
不过，这个优化思路与中点画线法的思想差别有点大。

借用泉的笔记：

如果按照中点画线法的优化思路应该改写为如下：

d = 1.25 -r

改为 4*d = 5 - 4r

然后d(新) = 4d（旧）

多边形的扫描转换与区域填充

最好自己看看PPT，我简要解释

多边形的扫描转换是什么？

多边形两种重要的表示方法：

顶点表示：用多边形的顶点序列来表示：直观，占内存少，便于几何变换，不能用于面着色
点阵表示：用位于多边形内部的像素几何刻画：便于帧缓冲器表示图形且是面着色所需的多边形表示形式

多边形的扫描转换就是把多边形的顶点表示转换为点阵表示

扫描算法（推荐看PPT）

核心思想：按扫描线顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的象素，即完成填充工作

所需数据结构：

活性表AET

新边表NET

具体看PPT

需要注意的是：如何正确处理交点的取舍。

算法步骤：

创建新边表NET；
把新边表NET［i］中的边结点，用插入排序法插入活性边表 AET，使之按X坐标递增顺序排序；
遍历AET表，把配对交点之间的区间(左闭右开)上的各象素(X，Y)，用drawpixel(x,y,color)改写象素颜色值；
遍历AET表，把Ymax=i的结点从AET表中删除，并把Ymax＞i 的结点的X值递增△X；
重复各扫描线。

优缺点：

优点：

对每个像素只访问一次
与设备无关

缺点：

数据结构复杂
只适合软件实现

边界标志算法

核心思想：

帧缓冲器中对多边形的每条边进行直线扫描转换，亦即对多边形边界所经过的象素打上标志，然后再采用和扫描线算法类似的方法将位于多边形内的各个区段着上所需颜色

伪代码：

void edgemark_fill(polydef, color)
多边形定义  polydef；   
int color;
{
	对多边形polydef每条边进行直线扫描转换；
	inside = FALSE;
	for (每条与多边形polydef相交的扫描线y )
		for (扫描线上每个象素x ) {
			if (象素 x 被打上边标志)
				inside = ! (inside);
			if (inside！ = FALSE)
				drawpixel (x, y, color);
			else drawpixel (x, y, background);
		}
}

区域填充算法

连通的类型：

4连通
8连通

种子填充算法：相当于深度优先搜索算法（不讲）

扫描线算法：个人理解：按照扫描线为单位进行搜索，减少了不必要的压栈弹栈，增加算法效率。

字符

字符集：

国际上最流行的字符集： ASCII码，用7位二进制数进行编码表示128个字符

汉字编码的标准字符集：GB2312－80，分为94个区，94个位，每个符号由一个区码和一个位码共同标识

字符类型：

点阵字符：轮廓压缩法
矢量字符

裁剪

类型：

直线段裁剪
多边形裁剪
字符裁剪

直线段裁剪

直接求交算法：简单粗暴

Cohen-Sutherland裁剪：将正方形显示区域分割成9个区域，然后分别编码，利用二进制的运算可以快速判断是否全在显示区域内或全部都在显示区域外。

中点分割裁剪算法：改进了Cohen-Sutherland裁剪中最坏要求4次交点的情况，使用中点简化情况。该算法具有二分的特点，大大减少运算量。

梁友栋－Barsky算法：核心思想为求出直线与窗口边界的交点，利用距离判断出两个点，然后决定显示。

Nicholls-Lee-Nicholl算法：考试不做要求，感兴趣的可以自行查看。

多边形裁剪

太难了，看不懂。不知道会不会考。aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa>___<

逐边裁剪法
Weiler-Athenton算法

逐边裁剪法（掌握思想）

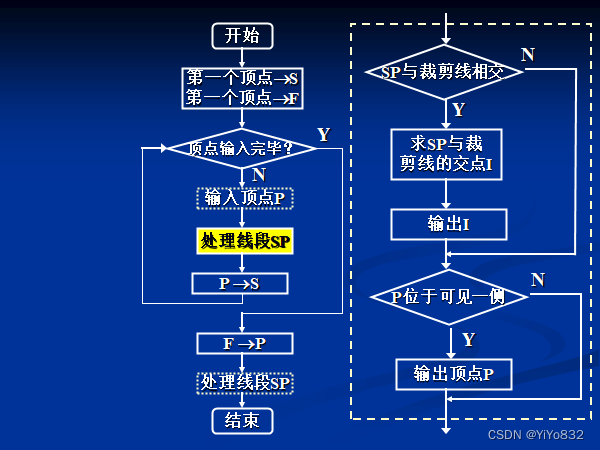
Weiler-Athenton算法（不要求）

算法的流程：

建立主多边形和裁剪多边形的顶点表；
求主多边形和裁剪多边形的交点，并将这些交点按顺序插入两多边形的顶点表中；相同交点间建立双向指针；

字符裁剪

串精度：将包围字串的外接矩形对窗口作裁剪,当字符串方框整个在窗口内时予以显示，否则不显示。
字符精度：将包围字的外接矩形对窗口作裁剪,当字符方框整个在窗口内时予以显示，否则不显示。
笔画\象素精度：将矢量字符的笔划分解成直线段对窗口作裁剪；将点阵字符像素相对窗口边界作取舍当字符方框整个在窗口内时予以显示，否则不显示。

反走样

走样是什么？

由于显示器的空间分辨率有限，因像素逼近误差，使所画图形产生畸变（台阶、锯齿）的现象

反走样是什么？

减少或消除走样的技术：硬件、软件的方法

反走样技术：

提高分辨率方法；
非加权区域采样；
加权区域采样；
半色调技术。

提高分辨率

方法如名字一样，不解释

区域采样（非加权/加权）

区域采样核心思想就是把直线模型改为长方形模型，使其有面积。

非加权采样：利用相交的面积决定像素的亮度值。

加权采样：

1、加入权函数，利用与像素中心点的距离计算亮度值。

2、为了简化计算，采用离散的计算的方式，计算亮度值。

eg：

太炫酷啦，伙计！图形学很神奇吧~~

半色调技术

在只有两级色调的情况下，牺牲分辨率增加色调级数。

对于两级灰度显示器可能构成的灰度数等于单元中像素个数加1；
若有m级灰度，n*n个像素组成一个单元，则灰度级别数为n*n*(m-1)+1

消隐

消隐概念：为了消除二义性，必须在绘制时消除被遮挡的不可见的线或面，习惯上称作消除隐藏线和隐藏面；

提高消隐算法效率的常见方法：

连贯性：相邻事物的属性之间有一定的连贯性，其属性值通常是平缓过渡的，如颜色值、空间位置关系等
包围盒技术：一个形体的包围盒指的是包围它的简单形体
背面剔除：
后向面：若多边形的外法向与投影方向（观察方向）的夹角为锐角（V· N>0），称为后向面（背面）。

后向面总是看不见的，不会由于后向面的遮挡，而使别的棱成为不可见的。因此计算时，可以把这些后向面全部去掉，这并不影响消隐结果。

空间分割技术：将投影平面上的窗口分成若干小区域；为每个小区域建立相关物体表，表中物体的投影于该区域有相交部分；则在小区域中判断那个物体可见时，只要对该区域的相关物体表中的物体进行比较即可
物体分层表示：模型变换中的树形表示方式；

消除隐藏线

算法

1️⃣ 若线段的两端点及视点在给定平面的同侧，线段不被给定平面遮挡，转(7)；

2️⃣ 若线段的投影与平面投影的包围盒无交，线段不被给定平面遮挡，转(7)；

3️⃣ 求直线与相应无穷平面的交：

•无交点转(4)；

•若交点在线段内部，交点将线段分成两段，与视点同侧一段不被遮挡，另一段在视点异侧转(4)；

•若交点在线段外部,转(4)。

4️⃣ 求所剩线段的投影与平面边界投影的所有交点。若无交点，转(7)。

5️⃣ 以上所求得的各交点将线段的投影分成若干段，求出第一段中点。

6️⃣ 若第一段中点在平面的投影内，则相应的段被遮挡，否则不被遮挡；其他段的遮挡关系可依次交替取值进行判断。

7️⃣ 结束。

消除隐藏面

画家算法
Z缓冲算法
扫描线Z缓冲算法
区间扫描线算法
区域子分割(Warnack)算法
光线投射算法

这几个算法难的不行，看不懂~~

画家算法

列表优先算法：画家的作画顺序暗示出所画物体之间的相互遮挡关系。

基本思想
1️⃣ 先把屏幕置成背景色；

2️⃣ 再把物体的各个面按其离视点的远近进行排序，排序结果存在一张深度优先级表中；

3️⃣ 然后按照从远到近的顺序逐个绘制各个面。

关键是如何对场景中的物体按深度排序。

优点：简单（如何对场景中的物体按深度排序）。

缺点：只能处理互不相交的面，且深度优先级表中面的顺序可能出错

Z缓冲算法

Z-Buffer算法（）
{ 	
	帧缓存全置为背景色
	深度缓存全置为最小Z值
	for(每一个多边形)
	{   
		扫描转换该多边形
	    for(该多边形所覆盖的每个象素(x,y) )
	   {	
	   		计算该多边形在该象素的深度值Z(x,y);
			if(Z(x,y)大于Z缓存在(x,y)的值)
			{    
				把Z(x,y)存入Z缓存中(x,y)处
				把多边形在(x,y)处的颜色值存入帧缓存的(x,y)处
			}	
	  }                       
     }                                                
}

优点：

简单稳定，利于硬件实现；
不需要整个场景的几何数据。

缺点:

空间：需要一个额外的Z缓冲器；
时间：在每个多边形占据的每个像素处都要计算深度值。

改进算法：先像素后多边形

{
	帧缓存全置为背景色
	for (屏幕上的每个象素(i, j)) {
		深度缓存变量zb置最小值MinValue
		for (多面体上的每个多边形Pk) {
			if (象素点(i, j)在Pk的投影多边形之内) {
				计算Pk在(i, j)处的深度值depth;
				if (depth大于zb) {
					zb = depth;
					indexp = k;
				}
			}
		}
		if (zb != MinValue)
			在交点 (i, j) 处用多边形Pindexp的颜色显示
		}
}

扫面线Z缓冲算法

扫描线Z - buffer算法() {
	建多边形y表；根据多边形顶点最小y值，将多边形置入多边形y表。
	活化多边形表APT，活化边对表AET初始化为空。
	For(每条扫描线i，i从小到大) {
		1. 帧缓存CB置为背景色。
		2. 深度缓存ZB (一维数组) 置为负无穷大。
		3. 将对应扫描线i的，多边形Y表中的多边形加入到活化多边形表APT中。
		4. 对新加入的多边形，生成其相应的边表。
		5. 对APT中每一个多边形，若其边表中对应扫描线i增加了新的边，将新的边配对，加到活化边对表AET中。
		6. 对AET中的每一对边：
			6.1 对xl < j < xr 的每一个象素，按增量公式z = z + ? za计算各点depth 。
		    6.2 与ZB中的量比较，depth > ZB(j), 则令ZB(j) = depth，并确定颜色
		                值，写帧缓存。
		7. 删除APT中多边形顶点最大y坐标为i的多边形，并删除相应的边。
		8. 对AET中的每一个边对，作如下处理：
		    8.1 删除ylmax或yrmax 已等于i的边。若一边对中只删除了其中一边，
		        对该多边形的边重新配对。
		    8.2 用增量公式计算新的xl 、 xr 和zl
	}
}

优点：

将整个绘图窗口内的消隐问题分解到一条条扫描线上解决，使所需的Z-Buffer大大减少
计算深度值时，利用了面连贯性，只用了一个加法。

缺点：

每个像素处都计算深度值，甚至不止一次的计算（多边形重叠区域），运算量仍然很大。

区间扫面线算法

基本思想

把当前扫描线与各多边形在投影平面的投影的交点进行排序后，使扫描线分为若干子区间。只要在区间任一点处找出在该处z值最大的一个面，这个区间上的每一个象素就用这个面的颜色来显示。

for (绘图窗口内的每一条扫描线）
{   求投影与当前扫描线相交的所有多边形
     求上述多边形中投影与当前扫描线相交的所有边，将它们记录在活化边表AEL中
     求AEL中每条边的投影与扫描线的交点；
     按交点的u坐标将AEL中各边从左到右排序，  两两配对组成一个区间；
      for （AEL中每个区间）
       {
          求覆盖该区间的所有多边形，将它们记入活化多边形表APL中；
          在区间上任取一点，计算APL中各多边形在该点的深度值，记深度最大者为P；
           用多边形P的颜色填充该区间
        }
}

区域子分割(Warnack)算法

基本思想

首先将场景中的多边形投影到绘图窗口内，判断窗口是否足够简单，若是则算法结束；否则将窗口进一步分为四块。对此四个小窗口重复上述过程，直到窗口仅为一个像素大小。此时可能有多个多边形覆盖了该像素，计算它们的深度值，以最近的颜色显示该像素即可。

光线投射算法

基本思想：

考察由视点出发穿过观察屏幕一象素而射入场景的一条射线，则可确定出场景中与该射线相交的物体；
在计算出光线与物体表面的交点之后，离象素最近的交点的所在面片的颜色为该象素的颜色；
如果没有交点，说明没有多边形的投影覆盖此象素，用背景色显示它即可。

for屏幕上的每一象素
  {形成通过该屏幕象素(u,v)的射线；
	 for 场景中的每个物体
         {将射线与该物体求交；
		if 存在交点
		     以最近的交点所属的颜色显示象素(u,v)
		 else
		      以背景色显示象素(u,v)
	    }
    }

第三章

参数曲线与曲面

描述物体的三维模型:

线框模型
曲面模型
实体模型

基本概念

主要涉及一些基本概念，比如曲线曲面的参数表示，切线，法线，法平面，密切平面，从切平面，曲率，挠率等等等。其实就是高数教的那些东西，估计也不会考，不再赘述，感兴趣可自行查阅高数书。

插值、拟合和光顺

插值：给定一组有序的数据点Pi构造一条曲线顺序通过这些数据点，所构造的曲线称为插值曲线。
拟合：构造一条曲线使之在某种意义下最接近给定的数据点，所构造的曲线为拟合曲线。
光顺(Fairing)：指曲线的拐点不能太多。对平面曲线而言，相对光顺的条件是

a. 具有二阶几何连续性(G2)
b. 不存在多余拐点和奇异点；
c. 曲率变化较小。

在图形学中，逼近包含了插值和拟合。

参数化

均匀参数化
累加弦长参数化
向心参数化
修正弦长参数化

连续性

简单理解：

参数连续性为在连接处，不仅切线的方向一致，而且切线斜率大小也一样。

而几何连续性为在连接处，方向一致，大小不等。

Bezier 曲线与曲面

可以看我写的了解一下都讲了什么，但要看懂还是得看PPT或者泉的笔记。这一部分确实好难懂/*—*\

是什么？

按照我的学习理解，可以理解为把所有控制点给予一定的权重，其中权重就是基函数。同时，可以注意到，该公式与所有的控制点都有关系。

Bernstein基函数的性质

正性
端点性质
权性
对称性
递推性：高一次的Bernstein基函数可由两个低一次Bernstein基函数线性组合而成

导函数
最大值：在i/n处最大
积分
升阶公式

Bezier曲线的性质

端点性质
Bezier曲线的起点、终点与相应的特征多边形的起点、终点重合。
起点和终点处的切线方向和特征多边形的第一条边及最后一条边的走向一致
r阶导矢只与（r+1）个相邻点有关
k阶导函数的差分

对称性

凸包性
几何不变性
变差缩减性
仿射不变性

de Casteljau递推算法

Bezier曲线的拼接（略）

非重点复习，同时我也看不懂

Bezier曲线的升阶和降阶（重点掌握升阶）

升阶核心公式：

升阶示意图如下：

降阶公式如下：

降阶时，选择一个递推公式即可

Bezier曲面

掌握递推公式即可：

Bezier曲线缺点：

缺少灵活性
控制性差
不易修改

B样条曲线与曲面

是什么？

de Boor-Cox递推

基函数性质

局部支撑性
权性
微分公式
非负性

如果节点数目是(m+1),函数的阶数是k,控制点的个数是(n+1)，则m=(n+k)，即节点数等于控制点数+阶数

分类

均匀样条曲线
准均匀样条曲线
分段Bezier曲线
一般的非均匀B样条曲线

B样条性质

局部性
开曲线定义域
凸包性
Bezier曲线是B样条曲线的特例
分段参数多项式
连续性
导数公式
变差缩减性
仿射不变性
几何不变性
直线保持性
造型灵活性

De Door算法

三次B样条的Bezier表示（略）

节点插入算法

B样条曲面（略）

三角网格

形体表示方法：

线框模型
实体模型
表面模型

三角网络概念

用三角形组成面片列表近似三维模型；

三角网格描述

顶点几何信息
三角网络拓扑连接的信息
附加属性

三角网格模型的存储

文本：易于阅读和理解；(OBJ和PLY文件格式)
二进制：具有较高的编码效率。

三角网格的半边表示（略）

网格处理概述

网络处理包括以下：

简化：用较少面片表示几何，提高绘制效率；
细分：以原始网格为基础，按一定规则生成包含更多面片的几何；
重剖：为了获得更规则的网格模型，可能具有更少或更多的面片。

光顺
参数化
网格修复：因为数据采集和配准存在误差
网格变形
网格分割
网格分析
模型检索

网格简化

顶点删除操作
边压缩操作
面片收缩操作
几何形状过渡

网格细分

Loop细分法
Butterfly细分。

特征敏感网格重剖

在网格简化后的模型中，三角形形状的规则性难以有较好的保证；网格重剖：生成较规则的网格模型，并尽可能与原网格在几何上相近。

特阵区域:具有至少一个较大主曲率的区域

第四章

真实图像的生成（略）

颜色视觉

光源分类

点光源
线光源
面光源

颜色

非彩色只有一个属性：明度
彩色有三个属性：色调(Hue) ；饱和度(Saturation) ；亮度(Value）

同时，颜色的物理属性有

主波长（Dominant Wavelength)：产生颜色光的波长，对应于视觉感知的色调；

纯度(Purity)：对应于饱和度；

明度(Luminance)：对应于光的亮度。

颜色视觉理论

简要看看了解三色学说，四色学说啥的（基本属于常识范围内的了）

CIE色度图（略）

常用颜色模型

RGB模型
CMY模型
HSV模型

简单光照明模型

Phong光照明模型

单光照明模型模拟物体表面对光的反射作用，不考虑折射。

增量式光照明模型

不同法向的多边形邻接处光强突变且有马赫带效应.

增量式光照明模型：

在每个多边形顶点处计算光照明强度或参数，然后在各个多边形内部进行双线性插值，得到多边形光滑均匀颜色分布
保证多边形之间的颜色光滑过渡。

两个主要算法（掌握步骤）

双线性法向插值：Phong明暗处理
双线性光强插值：Gouraud明暗处理

Gouraud明暗处理的步骤：

求出多边形顶点的平均法向。
使用Phong光照明模型计算顶点的平均光强。
利用线性插值，计算多边形各边上的像素的光强。
利用线性插值，计算多边形区域内各像素的光强。

Phong明暗处理的步骤：

计算各顶点的平均法向。
利用线性插值，计算多边形各边上的像素的法向。
利用线性插值，计算多边形区域内各像素的法向。
利用光强是法向量的函数（简单光照明模型），计算各点的光强。

对比：

阴影

阴影分类：

自身阴影
投影阴影

纹理及纹理映射（掌握概念）

纹理概述

纹理：物体表面的微小结构

从三方面思考：

简单光照明模型：改变漫反射系数->改变颜色；改变物体表面法向量。
真实感图形学：图像纹理；函数纹理
二维图像纹理和三维物体之间的关系：纹理空间，景物空间，图像空间。

二维纹理映射：

获取和表示
映射
滤波

几何纹理：生成图像时，对曲面的法向量进行扰动。

20届期末考题

一、填空题

1.常见的三角网格存储格式包含和。

2.深度缓冲区算法两类需要存储器存储的信息分别是: 和。

3. 图形通常由点、线、面、体等要素和灰度、色彩、线型、线宽等要素组成。

4.非点光源生成的阴影由 _和组成。

5.典型的图形系统通常由哪三种设备组成: 、和。

6.投影变换有两种基本方式，分别是和。

7. OpenGL函数库主要分为哪三类: 、和。

8.在计算机图形学中，和都可视为逼近。

二、选择题

三、简答题

四、计算证明题

答案

填空

1.OBJ PLY

2.颜色深度值

3.几何非几何

4.本影半影

5.输入设备输出设备图形处理设备

6.透射投影平行投影（正投影）

7.核心库gl 实用库glu 工具库glut

8.拟合插值

选择

1.A

2.B

3.D

4.D

5.A

6.D

7.C

8.C

9.D

简答

3.Phong明暗处理的实质是法向插值。

基本思想：

1、求顶点的法向；

2、用线性插值的方式求线上的法向；

3、用线性插值的方式求面上的法向；

4、根据各个点的法向使用简单光照明模型来计算各个点的光强。

计算证明题

看代码画图：

（草图）

理论作业

第二章 （除了2-2，基本都能在前面找到，不再给出）

第三章 （答案老师发了，自查）

答案：

2-2：

字丑勿喷~~~~~~~~~~~

OpenGL

参考：

OpenGL知识点-优快云博客

和老师给的资料

基本概念

使用的光照模型是整体光照模型

两种物体着色模式：RGBA颜色模式、颜色索引模式

OpenGL主要有核心库，实用库，辅助库，工具库，Windows(X窗口)专用库， Win32 API函数库。其中最主要的核心库gl，实用库glu，工具库glut。

坐标变换

视图变换：从不同的位置去观察它。
模型变换：移动或者旋转它，可以放大或缩小它。
投影变换：透视投影（近大远小）和平行投影。
视口变换：希望把整个看到的图形画下来，但它只占据纸张的一部分，而不是全部。

glFrustum函数：将当前可视空间设置为透视投影空间
glOrtho函数：将当前的可视空间设置为正投影空间
gluPerspective():设置透视投影矩阵
glViewport：视口变换,两个参数定义了视口的左下角（0,0表示最左下方），后两个参数分别是宽度和高度。
gluLookAt：视图变换
glMatrixMode(GL_PROJECTION):模型视图和投影矩阵都有相应的堆栈，glMatrixMode来指定当前操作。
glScale* : 缩放物体

双缓冲技术

在存储器（很有可能是显存）中开辟两块区域，一块作为发送到显示器的数据，一块作为绘画的区域，在适当的时候交换它们。

glutInitDisplayMode (GLUT_ RGB| GLUT_SINGLE);

GLUT_SINGLE:单缓冲

GLUT_DOUBLE:双缓冲

glutIdleFunc:在CPU空闲的时间调用某一函数

glutDisplayFunc(&myDisplay)：如需绘制窗口，调用myDisplay函数

垂直同步技术

只有在显示器刷新时，才把绘制好的图象传输出去供显示

看代码画图

个人总结以下步骤：

先看显示屏的像素，是1024*1024啊，还是800*800；
看主函数中，将要绘制的窗口设置在那里，注意左上角是(0,0)；
看绘制窗口的大小。
在看glutDisplayFunc(&myDisplay)中myDisplay绘制的图像，注意窗口的中心点为（0，0）。
需要了解简单的绘制函数，下面进行总结

多边形：

glBegin(GL_POLYGON);// 绘制为多边形
glVertex2f(0.0f, 0.0f);
glVertex2f(0.5f, 0.0f);
glVertex2f(0.5f, 0.5f);
glVertex2f(0.0f, 0.5f);
glEnd();
 // 实际是一个矩形

圆：

void myDisplay(void)
{
    //画一个圆
    int i;
    glClear(GL_COLOR_BUFFER_BIT);
    glBegin(GL_POLYGON);//单个简单填充多边形
    for (i = 0; i < n; i++) {
        glVertex2f(R * cos(2 * Pi / n * i), R * sin(2 * Pi / n * i));
    }
    glEnd();
    glFlush();
}

画点：

void myDisplay(void)
{
    glClear(GL_COLOR_BUFFER_BIT);
    glPointSize(5.0f);
    glBegin(GL_POINTS);
    glVertex2f(0.0f, 0.0f);
    glVertex2f(0.5f, 0.5f);
    glEnd();
    glFlush();
}

颜色：

glColor3f(1.0f, 1.0f, 1.0f); // RGB,范围从0-1

考后

整张试卷难度不大，不过有部分小题没复习到。OpenGL考了之前没遇到过的代码。整体来说，老师挺好的。