COMPFEST 14 - Preliminary Online Mirror (Unrated, ICPC Rules, Teams Preferred) M. Moving Both Hands

 

 翻译：

Pak Chanek正在玩他最喜欢的一种棋盘游戏。在游戏中，有一个有向图，顶点为𝑁，边为𝑀。在图中，边𝑖连接两个不同的顶点𝑈𝑖和𝑉𝑖，长度为𝑊𝑖。通过使用𝑖-th边缘，可以从𝑈𝑖移动到𝑉𝑖，但不能从𝑉𝑖移动到𝑈𝑖。

要玩这个游戏，首先Pak Chanek必须把他的双手放在两个不同的顶点上。在一个动作中，他可以移动他的一只手到另一个顶点使用边。将一只手从顶点𝑈𝑖移动到顶点𝑉𝑖，Pak Chanek需要𝑊𝑖秒的时间。注意Pak Chanek一次只能移动一只手。当Pak Chanek的双手都在同一顶点时，游戏结束。

Pak Chanek有几个问题。对于每个𝑝满足2≤𝑝≤𝑁，你需要找出Pak Chanek结束游戏所需的最小时间(以秒为单位)，如果最初Pak Chanek的左手和右手放在顶点1和顶点𝑝上，或者报告如果不可能的话。

输入
第一行包含两个整数𝑁和𝑀(2≤𝑁≤105,0≤𝑀≤2⋅105)——图中顶点和边的数量。

下𝑀行包含三个整数的𝑖-th𝑈𝑖,𝑉𝑖,和𝑊𝑖(1≤𝑈𝑖,𝑉𝑖≤𝑁,𝑈𝑖≠𝑉𝑖,1≤𝑊𝑖≤109)——一个有向边,连接两个顶点𝑈𝑖和𝑉𝑖长度的𝑊𝑖。没有一对不同的边𝑖和𝑗使得𝑈𝑖=𝑈𝑗和𝑉𝑖=𝑉𝑗。

输出
输出包含𝑁−1个整数的行。𝑗-th整数表示Pak Chanek结束游戏所需的最小时间(以秒为单位)，如果最初Pak Chanek的左手和右手被放置在顶点1和顶点𝑗+1上，如果不可能，则放置在顶点−1上。

例子
inputCopy
5 7
1 2 2
2 4 1
4 1 4
2 5 3
5 4 1
5 2 4
2 1 1
outputCopy
1 -1 3 4
请注意
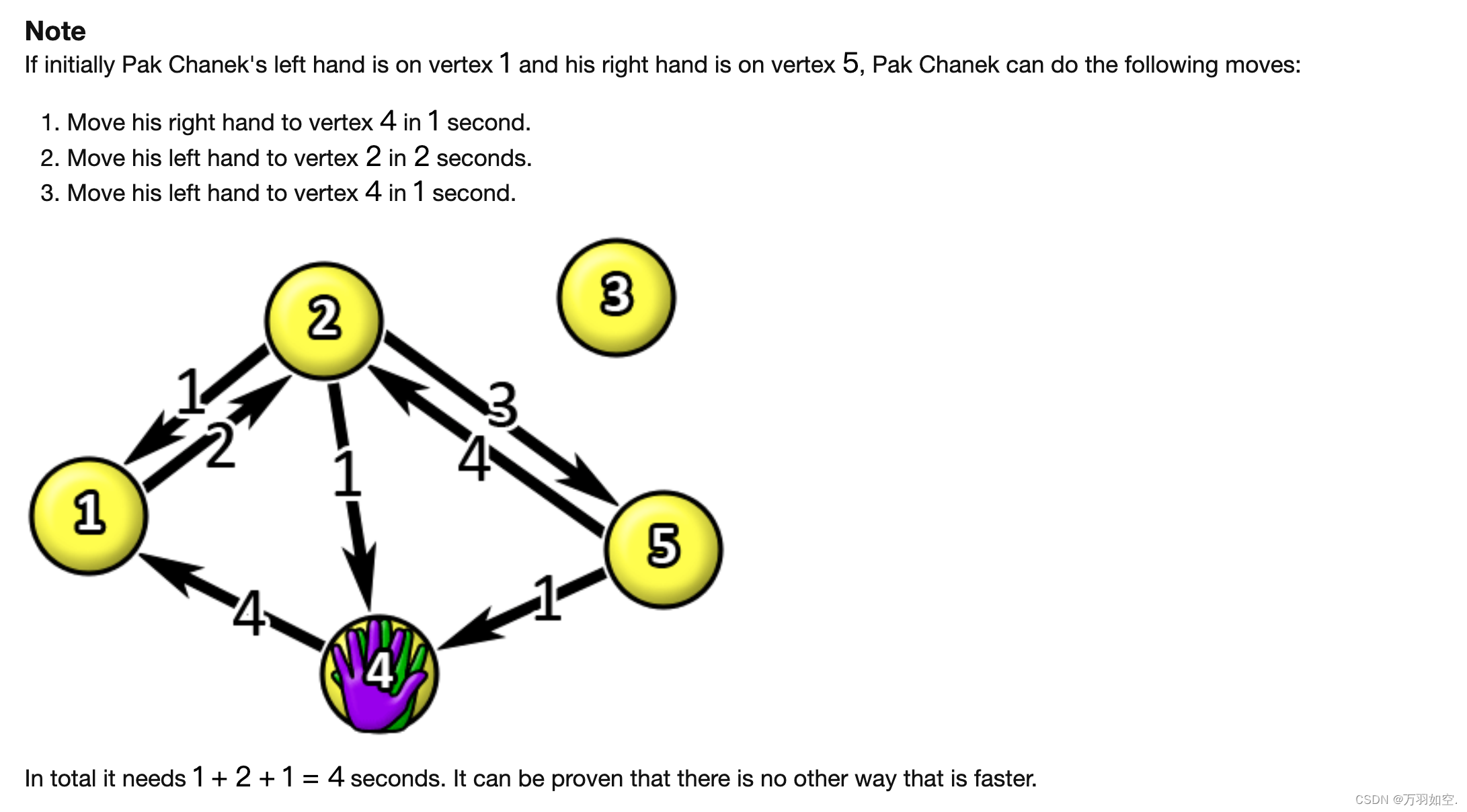
如果最初Pak Chanek的左手在顶点1上，他的右手在顶点5上，Pak Chanek可以做以下动作:

1秒内移动他的右手到顶点4。
2秒内将他的左手移到顶点2。
1秒内移动他的左手到顶点4。

总共需要1+2+1=4秒。可以证明没有其他方法比它更快。

思路：一个起点到很多点的的最短距离，单源最短路，用dijkstra建反向边，然后可以求解。感觉是一道很经典的最短路的图论题目。

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
using namespace::std;
typedef long long  ll;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
int n,m;
ll wa,ac;
vector<pair<ll, ll>>q[100005];
vector<pair<ll, ll>>w[100005];
ll a,b,c;
ll dis[100005][3];
int bj[100005];
void dijkstra(ll x){
    for (int i = 0; i<=n; i++) {
        dis[i][0]=dis[i][1]=1e18;
        bj[i]=0;
    }
    dis[x][1]=dis[x][0]=0;
    priority_queue< pair<ll, ll> ,vector<pair<ll, ll>>,greater<pair<ll, ll>>>ds;
    ds.push({0,1});
    ds.push({0,-1});
    while (!ds.empty()) {
        pair<ll,ll> kl=ds.top();ds.pop();
        ac=kl.first;wa=abs(kl.second);
        if (kl.second>0&&!(bj[wa]&1)) {
            bj[wa]|=1;
            for (auto k:q[wa]) {
                if (dis[k.first][0]>ac+k.second) {
                    dis[k.first][0]=ac+k.second;
                    ds.push({dis[k.first][0],k.first});
                }
            }
            for(auto k:w[wa]){
                if (dis[k.first][1]>ac+k.second) {
                    dis[k.first][1]=ac+k.second;
                    ds.push({dis[k.first][1],-k.first});
                }
            }
        }
        if (kl.second<0&&!(bj[wa]&2)) {
            bj[wa]|=2;
            for(auto k:w[wa]){
                if (dis[k.first][1]>ac+k.second) {
                    dis[k.first][1]=ac+k.second;
                    ds.push({dis[k.first][1],-k.first});
                }
            }
        }
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>n>>m;
    for(int i =1;i<=m;i++){
        cin>>a>>b>>c;
        q[a].push_back({b,c});
        w[b].push_back({a,c});
    }
    dijkstra(1);
    for (int i =2; i<=n; i++) {
        if (dis[i][0]==dis[i][1]&&dis[i][0]==1e18) {
            printf("-1 ");continue;
        }
        printf("%lld ",min(dis[i][1],dis[i][0]));
    }printf("\n");
    return 0;
}