数据结构【二叉树链式结构的实现、LeetCode刷题--8】

目录

1.1 二叉树链式结构

1.2 二叉树的前/中/后序遍历

1.3 二叉树节点数量

1.4 二叉树叶子节点个数

1.5 二叉树第k层节点个数

1.6  二叉树查找值为x的节点

1.7 二叉树深度

 1.8 二叉树销毁

2.1 层序遍历

2.2 判断二叉树是否是完全二叉树

3.1 Leetcode单值二叉树

3.2 Leetcode相同的树

3.3 LeetCode对称二叉树

3.4 LeetCode另一棵树的子树

3.5 二叉树的前序遍历

3.6 二叉树遍历_牛客题霸_牛客网

---

1.1 二叉树链式结构

当二叉树结构不是满或者完全二叉树时，二叉树实现用链式二叉树结构更适合

同时普通二叉树的增删查改无太大意义

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode	;

---

1.2 二叉树的前/中/后序遍历

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次

1. 前序遍历(Preorder Traversal 亦称先序遍历)—访问根结点的操作发生在遍历其左右子树之前。

2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

简化：前序：根 左子树 右子树        中序：左子树 根 右子树           后序：左子树 右子树  根

任何二叉树的结点都要化为根 左子树 右子树(前序时)，空树才不可再被分割的最小单位

void BinaryTreePrevOrder(BTNode* root)// 二叉树前序遍历 
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	printf("%d ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

void BinaryTreeInOrder(BTNode* root)// 二叉树中序遍历
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	BinaryTreeInOrder(root->left);
	printf("%d ", root->data);
	BinaryTreeInOrder(root->right);
}

void BinaryTreePostOrder(BTNode* root)// 二叉树后序遍历
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->data);
}

前序遍历递归思路图

1.3 二叉树节点数量

思路：

1.两种写法，一种使用全局变量count++统计，另一种采用分治方式

int count = 0;
void TreeSize1(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	count++;
	TreeSize1(root->left);
	TreeSize1(root->right);
}


int TreeSize2(BTNode* root)
{
	return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right) + 1;//分治，带返回值写法
}

右边就不递归了        

---

1.4 二叉树叶子节点个数

 大思路不变，如果为NULL树返回，如果为叶子节点返回，剩下的则不是叶子也不是空，继续递归

int BinaryTreeLeafSize(BTNode* root)// 二叉树叶子节点个数  分治带返回值方式写
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right == NULL)
		return 1;

	return BinaryTreeLeafSize(root->left)+ BinaryTreeLeafSize(root->right);//不是NULL也不是叶子节点

}

---

1.5 二叉树第k层节点个数

 二叉树第k层节点个数可以转换为左子树的第k-1层+右子树的第k-1层（子问题）

int BinaryTreeLevelKSize(BTNode* root, int k)// 二叉树第k层节点个数 (可以转换为左右子树k-1层)
{
	assert(k >= 1);
	if (root == NULL)
		return 0;

	if (k == 1)
		return 1;

	return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}

---

1.6  二叉树查找值为x的节点

注意：每次递归return返回值返回的是递归的上一层，而不是直接返回

用两个结点保存的好处是：可以判断返回值是否为结点或者NULL，如果为结点地址则依次返回，避免了找到结点后，再去递归从而浪费时间

当左子树都找完后没有找到结点，则继续去右子树寻找

假设我们要找的是4，递归展开图如下所示

---

1.7 二叉树深度

 思路：分治思想，算出左子树和右子树中的最大深度，比较即可得出最大深度

int TreeDepth(BTNode* root)
{
	if (root == NULL)
		return 0;

	int a = TreeDepth(root->left)+1;
	int b = TreeDepth(root->right)+1;
	return a > b ? a : b;
}

---

 1.8 二叉树销毁

 使用后序遍历销毁，先销毁左右子树再销毁根结点

void BinaryTreeDestory(BTNode* root)// 二叉树销毁
{
	if (root == NULL)
		return;

	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	//printf("%d \n", root ->data);
	free(root);
}

---

2.1 层序遍历

二叉树递归通常是深度优先遍历（DFS），先搜索最深的一条路径，再走分岔再回来，前序最符合深度优先

广度优先遍历（BFS）在二叉树中就是层序遍历（从根开始，一层一层遍历），一般借助队列辅助完成

 用队列辅助完成，出来后应该代入下一层结点，所以队列的typedef应该把数据类型改为二叉树指针

typedef struct BinaryTreeNode* QDataType;

void BinaryTreeLevelOrder(BTNode* root)// 层序遍历
{
	Queue q;
	QueueInit(&q);
	if (root)//root不为空，放数据
		QueuePush(&q,root);

	while (!QueueEmpty(&q))//如果队列不为空，则循环
	{
		BTNode* front = QueueFront(&q);//拿队头数据
		printf("%d ", front->data);
		QueuePop(&q);
		if (front->left)
			QueuePush(&q, front->left);

		if (front->right)
			QueuePush(&q, front->right);
	}

	QueueDestroy(&q);
}

---

2.2 判断二叉树是否是完全二叉树

思路：利用刚刚的层序遍历，把二叉树和空结点（#）打印出来，完全二叉树非空和空一定是间隔开的，是连续的值；如果其连续值中间存在#代表它不是完全二叉树

 

---

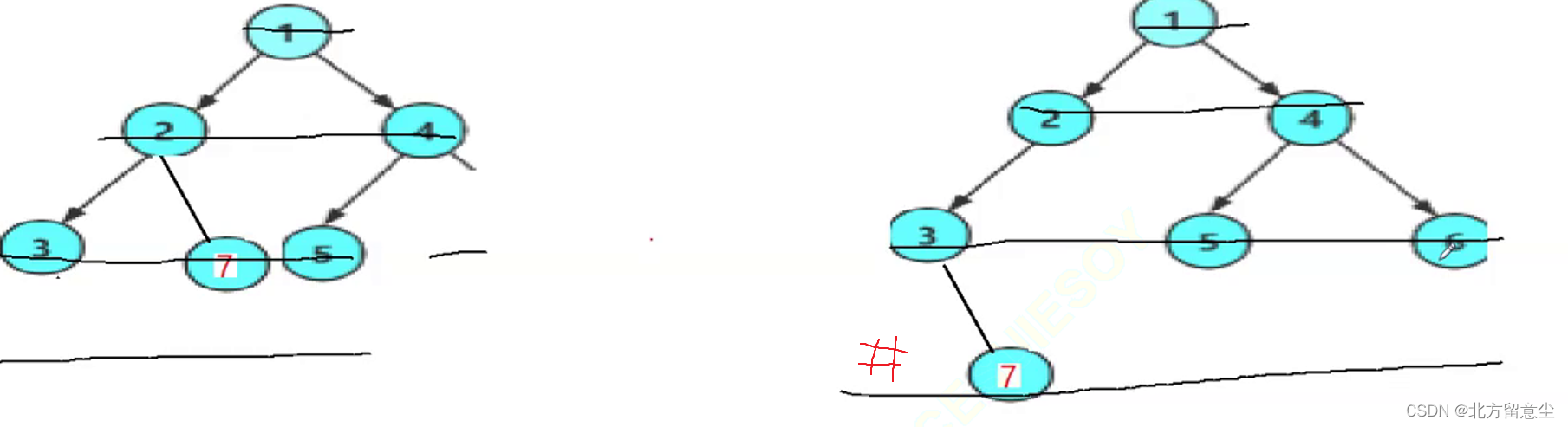
 做法：将刚刚层序遍历代码改下，把空也同样放入队列中，当取队头数据时取到了空，则代表此时队列里有可能是全空，也有可能包含非空结点，由于层序遍历完全二叉树性质：连续的值，如果有非空则代表此时是非完全二叉树

int BinaryTreeComplete(BTNode* root)// 判断二叉树是否是完全二叉树
{
	Queue q;
	QueueInit(&q);
	if (root)  //如果root为不为空则放数据
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);	
		QueuePop(&q);
		if (front)//空也放进去，直到取到的数据是空
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break;//遇到null则跳出来
		}
	}
	while (!QueueEmpty(&q))//两种情况，第一种是后面都为null，第二种是后面还有除null的值，为非完全二叉树
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)//第二种情况，为非完全二叉树
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;
}

---

3.1 Leetcode单值二叉树

思路：

1.结点和左右子树比较，如果相同则继续递归

2.爷爷和父亲比较，父亲和孩子比较，如果都相同则爷爷和父亲相同

bool isUnivalTree(struct TreeNode* root){
  if(root == NULL)
       return true;

    if(root->left && root->val != root->left->val)
    return false;

    if(root->right && root->val != root->right->val)
    return false;
    
    //剩下情况是根和孩子都相等
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

第二种写法：

思路：

1.拿结点作为基准值，遍历和每个结点值判断

2.其中要注意，如果一个结点值不等于基准值，则return返回给上一层，不然造成效率浪费

bool flag = true;
void TreeCopSame(struct TreeNode* root,int val)
{
    if(root == NULL || flag == false)
    {
        return;
    }


    if(root->val != val)
    {
        flag = false;
        return;
    }
    TreeCopSame(root->left,val);
    TreeCopSame(root->right,val);
}

bool isUnivalTree(struct TreeNode* root){
   if(root == NULL)
    return true;

    flag = true;
    TreeCopSame(root,root->val);
    return flag;
}

---

3.2 Leetcode相同的树

 思路：如果都为空，返回真；一个为空，为假；若均不为空，但是节点数值不一样，结果为假。

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
  if(p == NULL && q == NULL)
    return true;


    if(p == NULL && q != NULL)
    return false;


    if(p != NULL && q == NULL)
    return false;


  if(p->val != q->val)
    return false;


   return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

---

3.3 LeetCode对称二叉树

思路：

1.思路还是比较不相同，最后剩可递归条件

2.得再写个函数，比较和左子树右子树，再转化为根与根比较，左树的左子树与右树的右子树比较，左树的右子树与右树的左子树比较

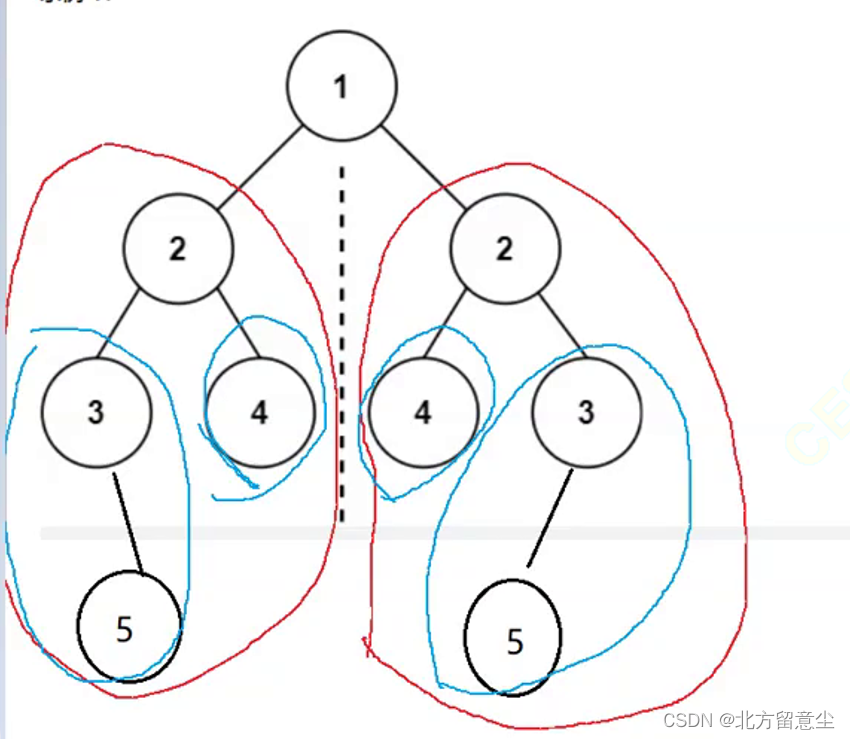
bool isSameTree(struct TreeNode* root1,struct TreeNode* root2)
{
    if(root1 == NULL && root2 == NULL)
    return true;

    if(root1 == NULL || root2 == NULL)//root1 为NULL，root2不为空；或者root1不为空，root2为空
    return false;

    if(root1->val != root2->val)
    return false;

    return isSameTree(root1->left,root2->right) && isSameTree(root1->right,root2->left);
}

bool isSymmetric(struct TreeNode* root){
 if(root == NULL)
 return true;

return isSameTree(root->left,root->right);
}

---

3.4 LeetCode另一棵树的子树

思路:

1.让每个结点都成为祖先结点，和subRoot相比较

2.复用相同的树，如果比较成功则返回true，最后只要有true结果就为true

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
  if(p == NULL && q == NULL)
    return true;

    if(p == NULL && q != NULL)
    return false;

    if(p != NULL && q == NULL)
    return false;

  if(p->val != q->val)
    return false;

   return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){

    if(root == NULL)
        return false;
 
    if(isSameTree(root,subRoot))//遍历，与root中所有子树都比较一遍
    return true;

    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot); //不为true便继续遍历左子树和右子树
}

---

3.5 二叉树的前序遍历

1.此题要求我们malloc开辟数组并返回前序遍历后的值，returnsize是我们指定的数组大小，要求我们解应用赋值，Leetcode接收数组大小值

2.依次把树中的值放入数组中去，递归左右子树，同时注意每次放入都应该让pi++

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 :TreeSize(root->left) + TreeSize(root->right) + 1;
}

void preoreder(struct TreeNode* root,int* a,int* pi)
{
    if(root == NULL)
    return;

    a[(*pi)++] = root->val; 
    preoreder(root->left,a,pi);
    preoreder(root->right,a,pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(*returnSize*sizeof(int));
    int i = 0;
    preoreder(root,a,&i);
    return a;

}

---

3.6 二叉树遍历_牛客题霸_牛客网

编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

思路：

1.先序遍历构建方式为：根，左子树，右子树，二叉树形状如下图所示

BTNode* CreateTree(char*arr,char* i)
{
    if(arr[*i] == '#')
    {
        (*i)++;
        return NULL;
    }
    BTNode* root = BuyNode(arr[(*i)++]);
    root->left = CreateTree(arr,i);
    root->right = CreateTree(arr,i);
    return root;
}

创建树的过程就是前序递归左右子树（把每个结点都看作拥有左右子树，知道最小问题NULL），把数组中的值，如果是#（NULL）则返回NULL，如果不为NULL，则创建树结点，最后return链接起来

 最后中序遍历打印即可

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef char BTDaataType;
typedef struct BTNodeTree
{
    struct BTNodeTree*left;
    struct BTNodeTree*right;
    int val;
}BTNode;

BTNode* BuyNode(BTDaataType x)
{
    BTNode * newnode = (BTNode*)malloc(sizeof(BTNode));
    assert(newnode);
    newnode->val = x;
    newnode->left = NULL;
    newnode->right = NULL;
    return newnode; 
}

BTNode* CreateTree(char*arr,char* i)
{
    if(arr[*i] == '#')
    {
        (*i)++;
        return NULL;
    }
    BTNode* root = BuyNode(arr[(*i)++]);
    root->left = CreateTree(arr,i);
    root->right = CreateTree(arr,i);
    return root;
}

void InOrder(BTNode* root)
{
    if(root == NULL)
        return;
    
   InOrder(root->left);
    printf("%c ",root->val);
   InOrder(root->right);
}

int main()
{
    char arr[100];
    scanf("%s",arr);
    char i = 0;
    BTNode* Tree = CreateTree(arr,&i);
    InOrder(Tree);
    return 0;
}