方法重载&可变个数形参&方法形参的值传递机制&递归方法（了解）

 * 一，方法的重载（overload） Loading
 * 
 * 1.概念：在一个类中允许，存在一个以上的同名方法，只要它们的参数个数或者参数类型不一                     样即可。
 *            （重名方法彼此之间称为重载的关系）
 *               总结为：“两同一不同”:同一个类，同一个方法名，参数列表不同，参数个数不同，参数类                                   型不同
 * 2.举例：
 *         Arrays类重载的sort()/binarySearch()
 * 
 * 3.判断是否是重载：
 *         跟方法的权限修饰符，返回值类型，形参变量名，方法体都没有关系！
 * 
 * 4.在通过对象调用方法时，如何确定某一个指定的方法：
 *         方法名————>参数列表

如下为代码示例：

public class OverLoadTest {
    public static void main(String[] args) {
        
        OverLoadTest test=new OverLoadTest();
        test.getSum(1,2);
    }
    
    //如下的四个方法构成了重载
    
    public void getSum(int i,int j) {
        System.out.println(i+j);
    }
    
    public void getSum(double d1,double d2) {
        
    }
    
    public void getSum(String s,int i) {
        
    }
    
    public void getSum(int i,String s) {
        
    }            //三四方法形参中顺序不同也属形参列表不同，可构成重载
    
//    public int getSum(int i,int j) {
//        
//        return 0;
//    }            //该方法与第一个方法返回值不同，但形参列表相同，不可以构成重载
    
//    public void getSum(int m,int n) {
//        
//    }            //该方法中形参变量名虽与第一个方法不同，但重载与变量名无关，所以不能构成重载。  
//    private void getSum(int i,int j) {
//        
//    }            //该方法与第一个方法权限修饰符不同，但形参列表一样，所以仍不能构成重载。
                //同理：方法体不同，形参列表相同仍不能构成重载

二，可变个数的形参

        1.jdk 5.0新增内容

        2.具体说明：

                2.1可变个数形参的格式：数据类型...变量名
                2.2当调用可变个数形参的方法时，传入的参数个数可以是：0个，1个，2个...
                2.3可变形参个数的方法与本类中方法名相同，形参不同的方法名之间构成重载
                2.4可变形参个数的方法与本类中方法名相同，形参不同的数组方法名之间不能构成重                          载，换句话说，它们不能同时存在。
                2.5可变个数的形参在方法中，必须声明在末尾。（否则调用的时候不能确定赋值给谁）
                2.6可变个数形参在方法中，最多只能声明一个可变形参。

        注：public void show(String[] strs){

               }与

               public void show(String...strs){

                }       不可以同时存在，因为它两表示同一个方法。

        如下为代码示例：

public class MethodArgsTest {
    
    public static void main(String[] args) {
          MethodArgsTest test=new MethodArgsTest();
          test.show(12);
          test.show("hello");
//        test.show("hello","world");
//        test.show("helloworld");
          test.show("aa","bb","cc");
    }

    public void show(int i) {
        
    }
    
    public void show(String s) {
        System.out.println("show(String)");
    }                //该方法和下面的方法可同时存在，认为他们的参数是不同的。
  
    public void show(String ...strs) {
        for(int i=0;i<strs.length;i++) {
            System.out.println(strs[i]);
        }
    }                //该方法中的String...strs就是可变个数的形参
    
//    private void show(String[] strs) {
//        
//    }
}

拓展：关于变量的赋值

        如果变量是基本数据类型，此时赋值的是变量所保存的数据值
        如果变量是引用数据类型，此时赋值的是变量所保存的数据的地址值。

        示例如下图

        

三，方法形参的值传递机制

 方法形参的传递机制，（叫）值传递

 1.形参：方法定义时，小括号内声明的参数
    实参：方法调用时，实际传递给形参的数据。（调用有形参的方法时，在括号内给形参赋的                     值） 
  2.值传递机制
       如果参数是基本数据类型，此时实参赋给形参的是实参真实存储的数据值(即下图中第                     18，19行中的m与n的值是多少就赋给第32行中的形参m，n为多少）
       如果参数是引用数据类型，此时实参赋给形参的是实参存储数据的地址值（含变量的数据类           型）

如下有两个实例：

  示例1：

内存解析的过程 ：

先是main方法在栈里有m：10和n：20，（m=10，n=20是属于main方法的）然后将m=10与n=20分别赋值给swap方法中的形参；则现在在栈中有属于swap方法的m=10，n=20；在swap方法中声明了新的变量temp，并使m的值赋给temp，然后将n的值赋给m，再将temp的值赋给n，则此时temp=10，m=20，n=10；这样之后swap方法执行完以后就弹出栈了，所以此时在main方法中执行输出语句，输出的是main方法中的m和n，即输出m=10，n=20。图示如下。

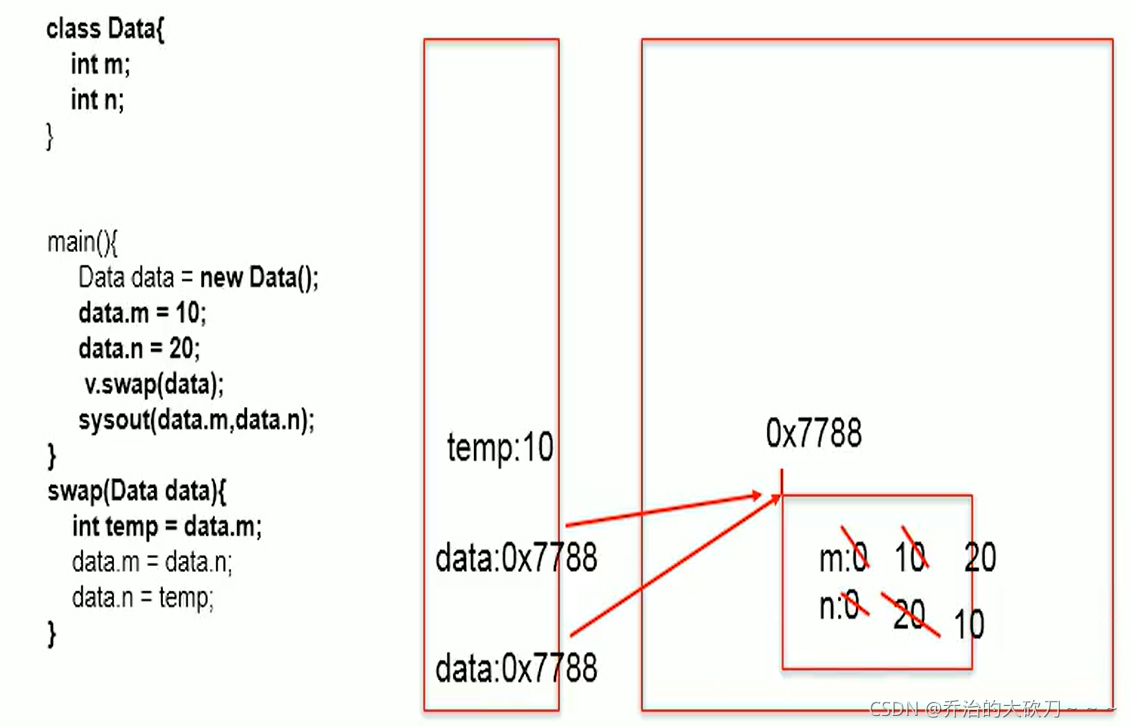
示例2：

内存解析：因为在整个操作中swap方法中的形参是引用数据类型，而test在调用swao方法时，是将创建的data对象复制给了形参data，所以此时形参中的data与对象data指向堆空间中的同一个地址值。所以执行输出语句后可得到m与n交换值后新的m与n。具体如下图。

应用：

四，递归方法（了解）

递归方法的使用（了解）
 * 1.递归方法：一个方法体内调用它自身
 * 2.方法递归包含了一种隐式的循环，它会重复执行某段代码，但这种重复执行无需代码控制。
 * 递归一定要向已知方向递归，否则这种递归就变成了无穷递归，类似于死循环。

代码例题如下：

public class RecursionTest {

	public static void main(String[] args) {
		
		//例1：计算1—n之间所有自然数的和
		//方式一：使用for循环
		int sum=0;
		for(int i=1;i<=100;i++) {
			sum+=i;
		}
		System.out.println(sum);
		
		//方式二：使用递归方法
		RecursionTest test=new RecursionTest();
		int sum1=test.getSum(100);
		System.out.println(sum1);
		
		int value=test.f(10);
		System.out.println(value);
	}
	
	public int getSum(int n) {
		if(n==1) {
			return 1;
		}else {
			return n+getSum(n-1);
		}
	}
	
	//例2：计算1—n之间所有自然数的乘积:n!
	public int getSum1(int n) {
		if(n==1) {
			return 1;
		}else {
			return n*getSum(n-1);
		}
	}
	
	//例3：已知有一个数列：f(o)=1.f(1)=4,f(n+2)=2*f(n+1)+f(n)
	//其中n是大于0的整数，求f(10)的值
	public int f(int n) {
		if(n==0) {
			return 1;
		}else if(n==1) {
			return 4;
		}else {
			return 2*f(n-1)+f(n-2);
		}
	}
}