一、插入排序
思想:
对于未排好序的数据,在已经排好序的序列中依次往后查找,找到相应位置并插入
日常生活中,我们打扑克所用的整理牌的方法就为 插入排序
当插入第i个元素的时候,前面的arr[i-1],ar[i-2]......arr[0]已经全部排序好,只需要用当前位置的元素arr[i]与arr[i-1],arr[i-2]......依次比较,找到插入位置将其插入即可
// 插入排序
void InsertSort(int* arr, int n)
{
//从第一个元素开始比较
for (int i = 1; i < n; ++i)
{
//让end保存当前元素的前一个位置
int end = i - 1;
//key保存当前元素
int key = arr[i];
//如果end>=0&&当前元素key小于前一个元素,前一个元素向后搬移,再使end--
while (end>=0 &&key<arr[end])
{
arr[end + 1] = arr[end];
end--;
}
//循环退出说明,此位置之前没有元素或者,此位置之前的元素都比key小
//插入key
arr[end + 1] = key;
}
}时间复杂度:
最好情况 O(n) 最坏情况O(n^2)
空间复杂度:O(1)
稳定性:稳定
二、希尔排序
思想:
先选定一个整数grp,然后根据这个数对数组分组,依次对分组的每一组数据进行插入排序,然后重复上述步骤,直到grp==1时结束(当grp==1时,相当于整个序列被分为1组,此时,只需进行一次插入排序即可)
// 希尔排序
void ShellSort(int* arr, int n)
{
//先选定一个整数
int grp = 5;
while (grp >=1)
{
//将数组以grp间隔 分开,依次排序每一个分开的组
for (int i = grp; i < n; ++i)
{
int end = i - grp;
int key = arr[i];
while (end >= 0 && key < arr[end])
{
arr[end + grp] = arr[end];
end -= grp;
}
arr[end + grp] = key;
}
grp-=2;
}
}时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
三、选择排序
思想:
从每次待排序的序列中选择出一个最小的元素,将其放在序列的起始位置,直到全部元素排列完
// 选择排序
void SelectSort(int* arr, int n)
{
//选择一个最小的值放在每次循环查找的第一位
for (int i = 0; i < n-1; ++i)
{
//每次更新 minpos 的位置
int minpos = i;
//在第i个元素和第n个元素之间找一个最小值
for (int j = i; j < n; ++j)
{
if (arr[minpos]>arr[j])
{
minpos = j;
}
}
//将最小值与第i个元素交换
if(minpos!=i)
{
Swap(&arr[i], &arr[minpos]);
}
}
}时间复杂度:
最坏情况:O(N^2) 最好情况:O(N^2)
空间复杂度: O(1)
稳定性:不稳定
直接选择排序思想非常好理解,但是效率不高,实际应用中很少使用
四、堆排序
思想:
利用堆的思想进行排序,总共分为俩个步骤:
1.建堆
升序建大堆,降序建小堆
建堆的时候要用到一种向下调整的方法来实现,具体实现看以下代码:
// 堆排序
//向下调整
void AdjustDwon(int* arr, int n, int root)
{
int child = 2 * root + 1;
while (child < n)
{
//右孩子存在且左孩子的值小于右孩子
//交换左右孩子
if (child + 1 < n && arr[child] < arr[child + 1])
{
Swap(&arr[child], &arr[child + 1]);
}
//双亲的值比左孩子小
if (arr[root]<arr[child])
{
//交换双亲和左孩子
//更新双亲和左孩子,使双亲指向左孩子,左孩子指向此时双亲的左孩子
Swap(&arr[child], &arr[root]);
root = child;
child = 2 * root + 1;
}
else
{
return;
}
}
}
void HeapSort(int* arr, int n)
{
//升序建大堆,降序建小堆
//以下为建大堆,进行升序序排序
for (int i = (n - 2) / 2; i >= 0; --i)
{
AdjustDwon(arr, n, i);
}
//每次循环将堆顶值和堆尾的值进行交换,在进行向下调整
while (n > 0)
{
Swap(&arr[0], &arr[n - 1]);
n--;
AdjustDwon(arr, n, 0);
}
}时间复杂度:O(N*logN)
空间复杂度:O(1)
稳定性:不稳定
五、冒泡排序
思想:
从数组的开始位置俩俩元素相比较,前一个比后一个大则交换俩元素位置,否则,继续向后比较
第一趟比较完,可以将数组中最大的元素放在数组结尾位置
依次循环比较n-1趟即可(n为数组元素个数)
// 冒泡排序
void BubbleSort(int* arr, int n)
{
for (int i = 0; i < n - 1; ++i)
{
for (int j = 0; j < n - 1 - i; ++j)
{
if (arr[j] > arr[j + 1])
{
Swap(&arr[j], &arr[j + 1]);
}
}
}
}时间复杂度:
最好情况:O(N) 最坏情况:O(N^2)
空间复杂度:O(1)
稳定性:稳定
六、快速排序
思想:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
快速排序寻找基准值下标有三种方法:
法一:hoare版本
思想:
1.选中数组中最后一个元素作为基准值
2.确定俩个指针,左指针指向数组最左边的元素,右指针指向数组结尾元素(刚开始右指针就指向基准值的位置)
3.从左指针指向的位置开始,依次与基准值进行比较,如果左指针指向的元素比基准值小,则左指针向后移动一位,否则,停止移动;左指针停止移动后,开始从右指针指向的位置开始比较,如果右指针指向位置的元素比基准值大,则右指针向左移动一位,否则,停止移动
4.循环上述步骤,直到左右指针相遇
5.返回左指针或者右指针位置下标
int PartSort1(int* arr, int left, int right)
{
//找到最后一个元素作为基准值
int key = arr[right - 1];
int begin = left, end = right - 1;
while (begin < end)
{
//循环存begin位置开始查找比基准值key大的元素
while (begin < end && arr[begin] <= key)
{
begin++;
}
//从end位置开始查找比基准值key小的元素
while (begin < end && arr[end] >= key)
{
end--;
}
//如果begin<end,则交换元素
if (begin < end)
{
Swap(&arr[begin], &arr[end]);
}
}
//上述循环退出,将基准值放在begin位置
if (begin != right - 1)
{
Swap(&arr[begin], &arr[right - 1]);
}
//返回基准值的位置
return begin;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
//区间中只有一个元素
if ((right - left) <= 1)
{
return;
}
else
{
//找到基准值位置p,基准值左侧元素都比基准值小,基准值右侧元素都比基准值大
int p = PartSort1(arr, left, right);
//递归排序基准值左侧 和 右侧
QuickSort(arr, left, p);
QuickSort(arr, p + 1, right);
}
}法二:挖坑法
思想:
挖坑法思想整体与第一种hoare相同
1.选中数组中最后一个元素作为基准值
2.确定俩个指针,左指针指向数组最左边的元素,右指针指向数组结尾元素(刚开始右指针就指向基准值的位置)
3.从左指针位置开始,依次向后与基准值进行比较,遇到比基准值大的,停止后移左指针,然后将此时左指针位置的元素放入右指针位置,在使右指针向前移动一位,此时左指针的位置就可以看为一个坑;然后从右指针开始继续与基准值进行比较,遇到比基准值小的元素停止移动,然后将此时右指针对应位置的元素,放入刚才左指针的位置,即将左指针对应的坑填满。
4.循环上述步骤,直到左右指针相遇
5.返回左指针或者右指针位置下标
// 快速排序挖坑法
int PartSort2(int* arr, int left, int right)
{
int begin=left, end = right - 1;
int key = arr[right - 1];
while (begin < end)
{
while (begin < end && arr[begin] <= key)
{
begin++;
}
if (begin < end)
{
arr[end] = arr[begin];
end--;
}
while (begin < end && arr[end] >= key)
{
end--;
}
if (begin < end)
{
arr[begin] = arr[end];
begin++;
}
}
arr[begin] = key;
return begin;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
//区间中只有一个元素
if ((right - left) <= 1)
{
return;
}
else
{
//找到基准值位置p,基准值左侧元素都比基准值小,基准值右侧元素都比基准值大
int p = PartSort2(arr, left, right);
//递归排序基准值左侧 和 右侧
QuickSort(arr, left, p);
QuickSort(arr, p + 1, right);
}
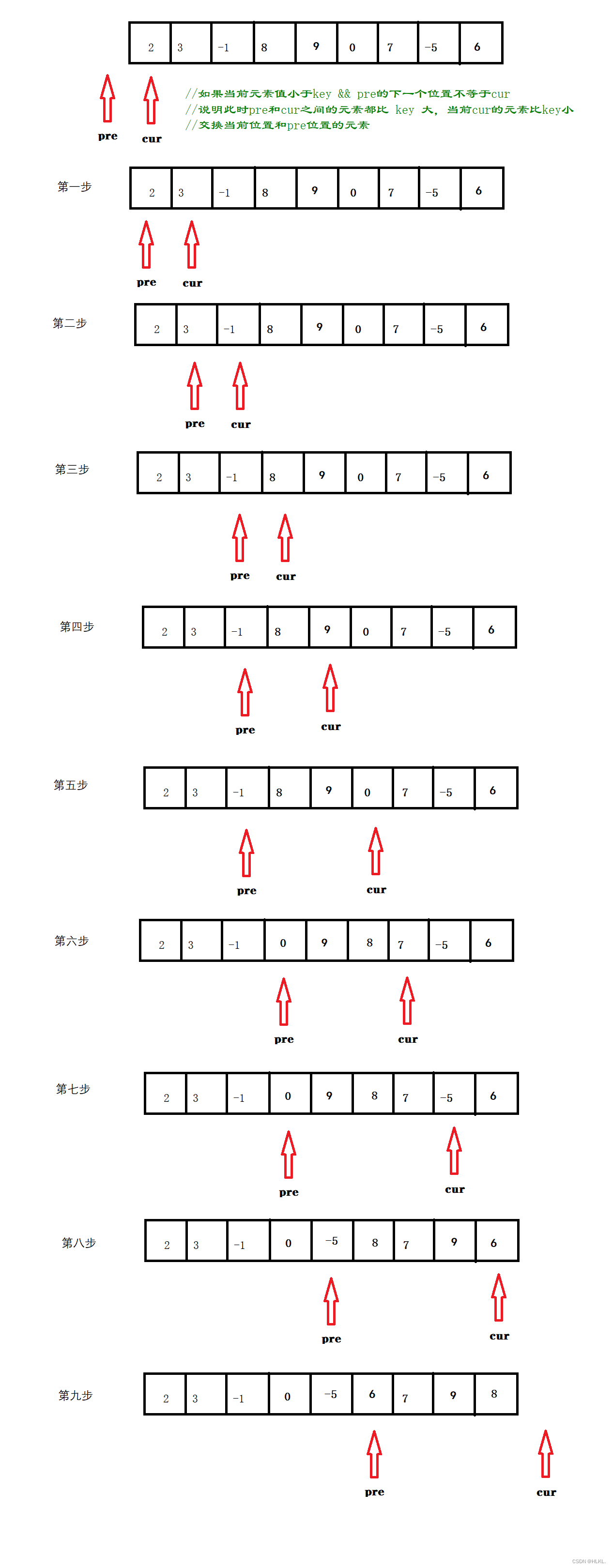
}法三:双指针法
具体实现步骤如下:
// 快速排序前后指针法
int PartSort3(int* arr, int left, int right)
{
//定义前后指针,指向left和left之前的位置
int cur = left;
int pre = cur - 1;
int key = arr[right - 1];
while (cur < right)
{
//如果当前元素值小于key && pre的下一个位置不等于cur
//说明此时pre和cur之间的元素都比 key 大,当前cur的元素比key小
//交换当前位置和pre位置的元素
if (arr[cur]<key && ++pre != cur)
{
Swap(&arr[cur], &arr[pre]);
}
//使当前位置向后移动
cur++;
}
if (++pre != right - 1)
{
Swap(&arr[pre], &arr[right - 1]);
}
return pre;
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
//区间中只有一个元素
if ((right - left) <= 1)
{
return;
}
else
{
//找到基准值位置p,基准值左侧元素都比基准值小,基准值右侧元素都比基准值大
int p = PartSort3(arr, left, right);
//递归排序基准值左侧 和 右侧
QuickSort(arr, left, p);
QuickSort(arr, p + 1, right);
}
}快速排序总结
时间复杂度:
最好情况:O(NlongN) 最坏情况:O(N^2)
空间复杂度:O(logN)
稳定性:不稳定
七、归并排序
思想:

void MergeSortData(int* arr, int left, int mid,int right, int* temp)
{
int begin1 = left, end1 = mid;
int begin2 = mid, end2 = right;
//index为每次递归进来temp的下标
int index = left;
//依次比较左右两部分的元素大小,将较小的放入temp中
while (begin1 < end1 && begin2 < end2)
{
if (arr[begin1] <= arr[begin2])
{
temp[index++] = arr[begin1++];
}
else
{
temp[index++] = arr[begin2++];
}
}
//右部分比较完,左半部分未比较完
while(begin1 < end1)
{
//交左半部分剩余的元素放入temp中
temp[index++] = arr[begin1++];
}
//同理
while(begin2 < end2)
{
temp[index++] = arr[begin2++];
}
}
void _MergeSort(int* arr, int left, int right, int* temp)
{
//区间中只有一个元素
if ((right - left) <= 1)
{
return;
}
else
{
int mid = left + ((right - left) >> 1);
//递归排序左右俩测
//左侧[left,mid)
_MergeSort(arr, left, mid, temp);
//右侧[mid.right)
_MergeSort(arr, mid, right, temp);
//将排好序的左右两侧 进行合并
MergeSortData(arr, left, mid, right, temp);
//将合并好的元素拷贝到原数组
memcpy(arr + left, temp + left, (right - left) * sizeof(int));
}
}归并排序总结
时间复杂度:O(NlongN)
空间复杂度:O(N)
稳定性:稳定
八、计数排序
计数排序在数据范围集中时,效率很高
步骤:
1.找到数组中最大元素max和最小元素min
2.申请空间数组Count,统计数组中每个元素出现的次数(Count(arr[i]-min)即为元素arr[i]出现的次数)
3.在数组Count中,Count[0]表示 arr数组中最小的元素出现的次数,Count[1]表示 arr数组中次小的元素出现的次数(这里可能并不是下标1,因为次小的元素与min的差值可能大于1).......依次类推
4.对每个元素进行回收,Count[i]不为0 的情况下,说明在arr数组中存在元素i+min,且出现Count[i]次,回收元素时候,依次从Count数组中不为0的元素中 最小的下标开始回收。
// 计数排序
void CountSort(int* arr, int n)
{
//找到最大值 和 最小值
int min = arr[0], max = arr[0];
for (int i = 1; i < n; ++i)
{
if (min > arr[i])
{
min = arr[i];
}
if (max < arr[i])
{
max = arr[i];
}
}
//以上数组中的元素处于 min~max这个区间内
//申请max-min+1个空间统计数组arr中每一个元素出现的次数
int rang = max - min + 1;
//申请空间,并全部初始化为0
int* Count=(int*)calloc(rang,sizeof(int));
//统计每个元素出现的次数
for (int i = 0; i < n; ++i)
{
Count[arr[i] - min]++;
}
//对每个元素进行回收
int size = 0;
for (int i = 0; i < rang; ++i)
{
//在Count数组元素不为0的情况下
//Count数组下标从小到大 依次是 arr数组中从小到大的元素出现的次数
while (Count[i] > 0)
{
arr[size++] = i + min;
Count[i]--;
}
}
free(Count);
}






















 863
863

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








