炫酷的js十大排序算法（下）

堆排序

堆排序算法是一种基于堆数据结构的排序算法，其核心思路在于将待排序数组看做二叉树，通过构建大顶堆或小顶堆来实现排序。对于大顶堆，每个节点的值均大于或等于它的子节点；对于小顶堆，每个节点的值均小于或等于它的子节点。排序时，取堆顶元素，将其存储到已排序数组中，并从堆中删除；然后重新调整剩余元素形成新的堆，重复以上操作直至所有元素排序完成

代码 

var len1; // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量
 
function buildMaxHeap(arr) {
  // 建立大顶堆
  len1 = arr.length;
  for (var i = Math.floor(len1 / 2); i >= 0; i--) {
    heapify(arr, i);
  }
}
 
function heapify(arr, i) {
  // 堆调整
  var left = 2 * i + 1,
    right = 2 * i + 2,
    largest = i;
 
  if (left < len && arr[left] > arr[largest]) {
    largest = left;
  }
 
  if (right < len && arr[right] > arr[largest]) {
    largest = right;
  }
 
  if (largest != i) {
    swap(arr, i, largest);
    heapify(arr, largest);
  }
}
 
function swap(arr, i, j) {
  var temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}
 
function heapSort(arr) {
  buildMaxHeap(arr);
 
  for (var i = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i);
    len--;
    heapify(arr, 0);
  }
  return arr;
}
 
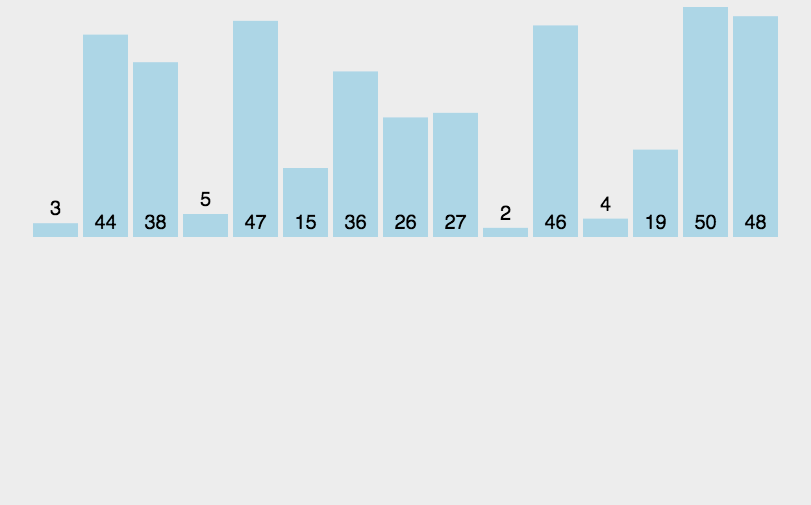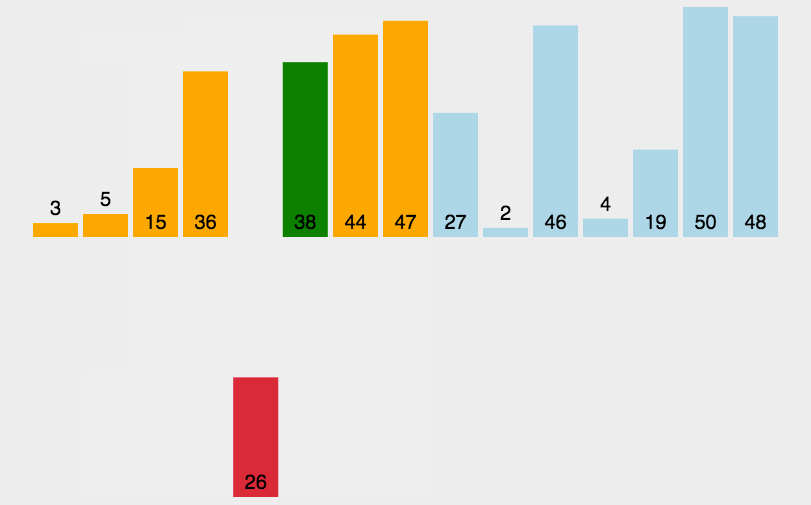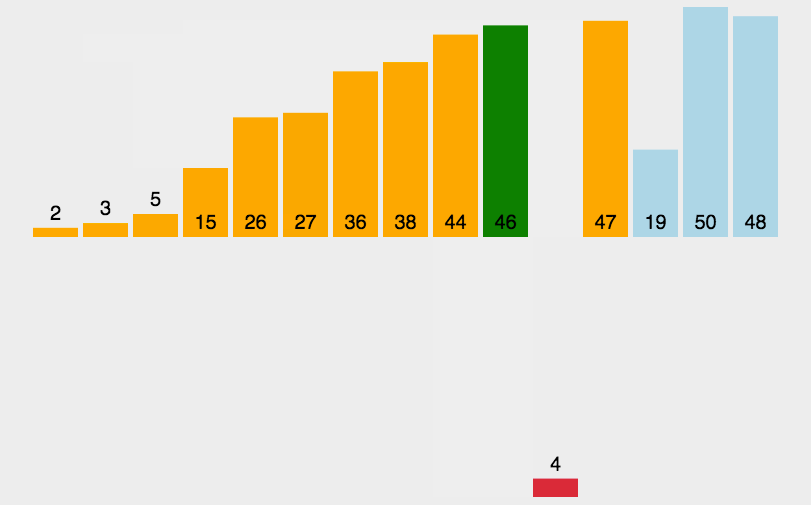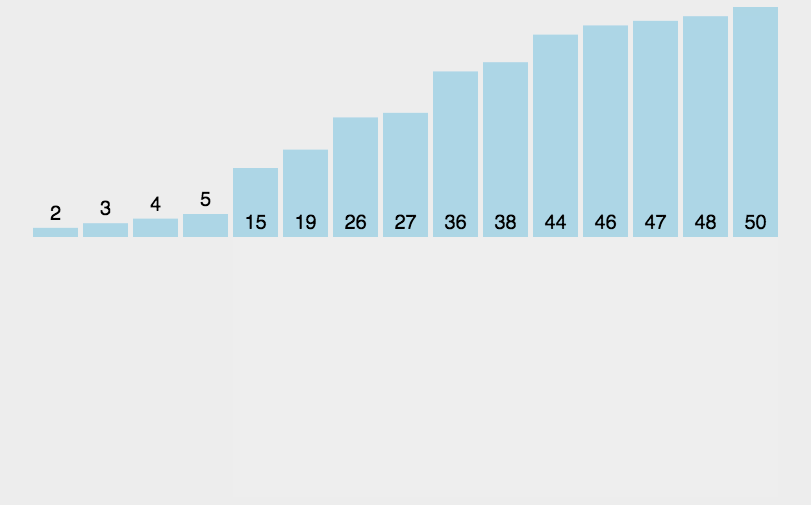
let arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 12, 46, 4, 19, 50, 48];
 
console.log(heapSort(arr)); // [3,  4,  5, 12, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

计数排序

计数排序（Counting Sort）是一种非基于比较的排序算法，其时间复杂度为O(n+k)，其中k表示待排序数组中最大元素与最小元素之差加1。该算法的基本思想是统计每个元素在待排序数组中出现的次数，然后根据统计结果构建有序序列。

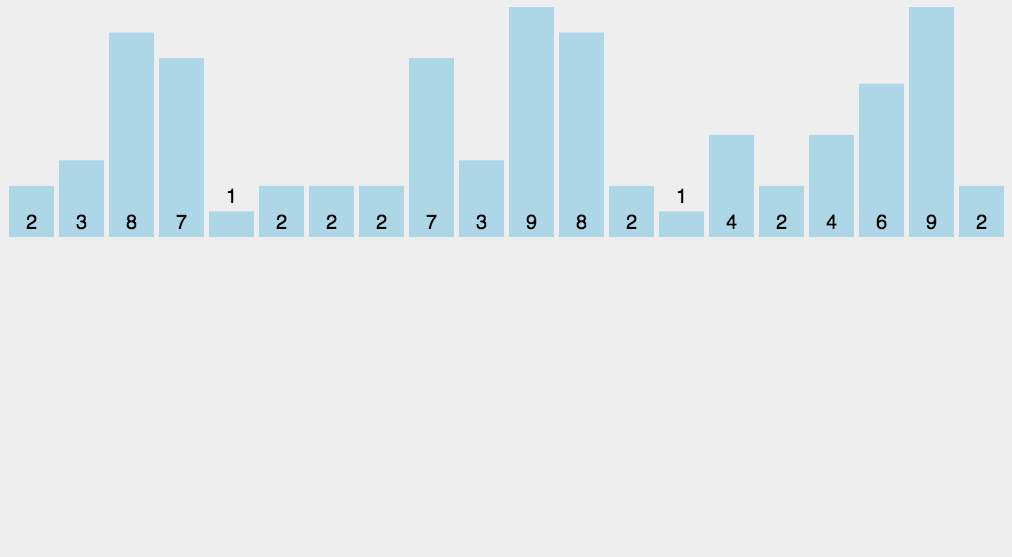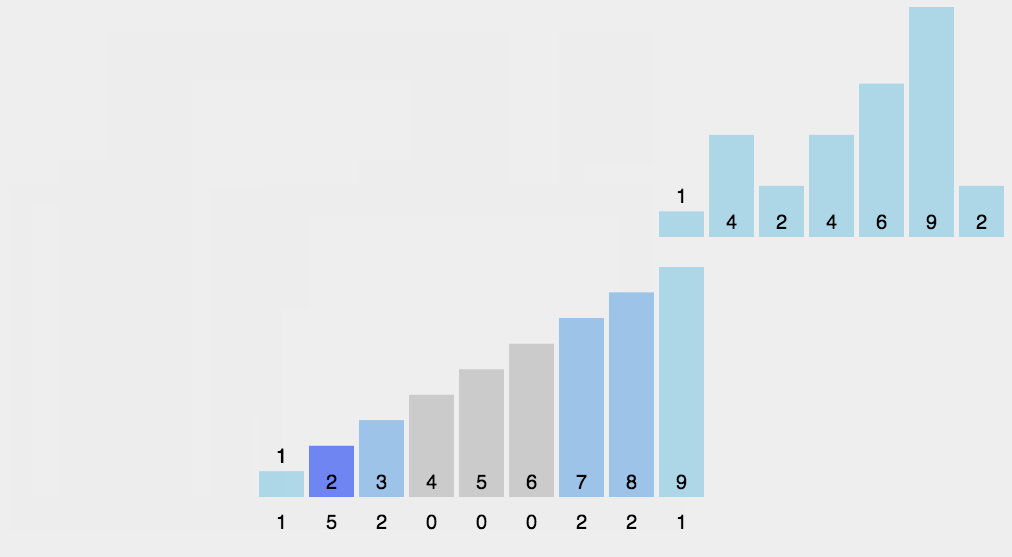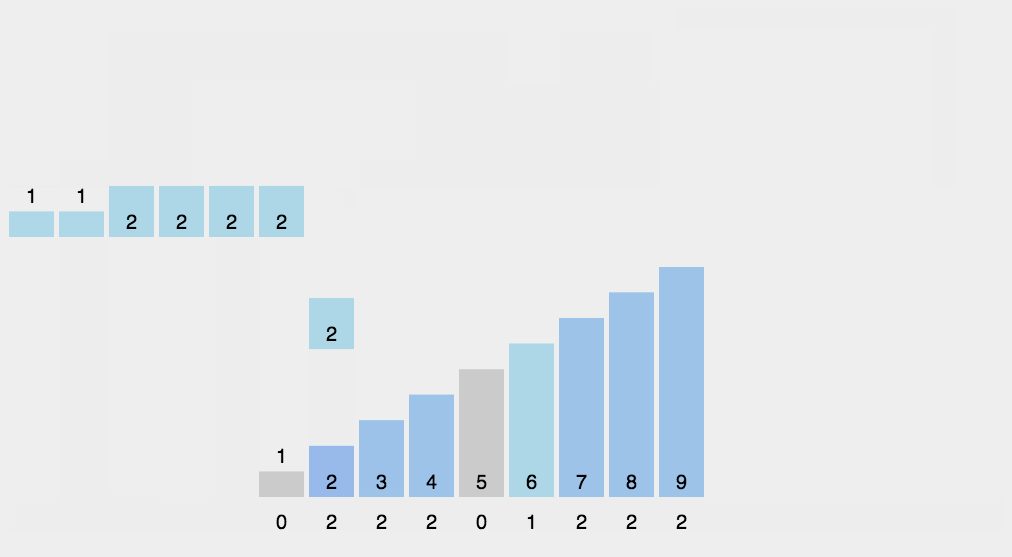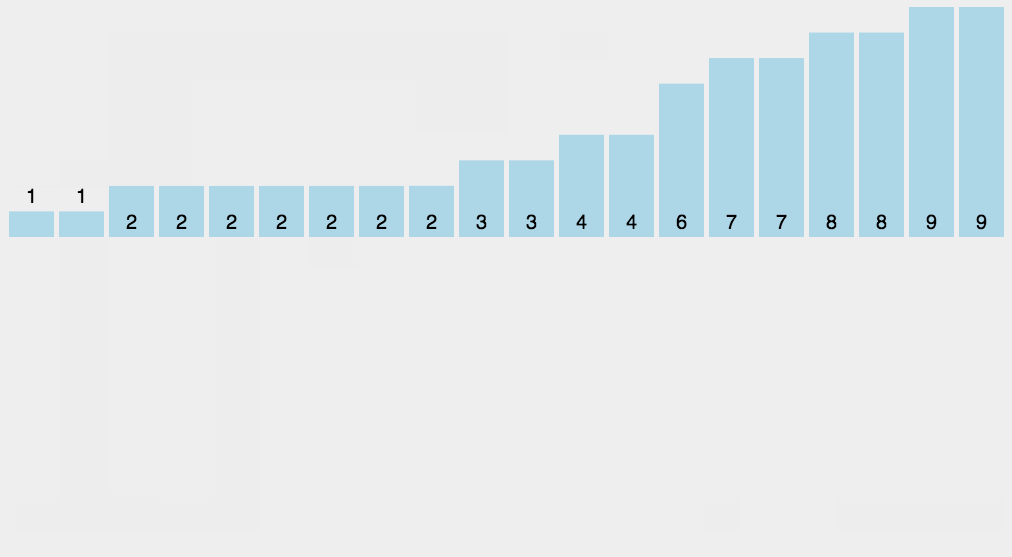
代码 

function countingSort(arr, maxValue) {
  var bucket = newArray(maxValue + 1),
    sortedIndex = 0;
  (arrLen = arr.length), (bucketLen = maxValue + 1);
 
  for (var i = 0; i < arrLen; i++) {
    if (!bucket[arr[i]]) {
      bucket[arr[i]] = 0;
    }
    bucket[arr[i]]++;
  }
 
  for (var j = 0; j < bucketLen; j++) {
    while (bucket[j] > 0) {
      arr[sortedIndex++] = j;
      bucket[j]--;
    }
  }
 
  return arr;
}

插入排序 

1、第一个元素默认已排好序，从第二个元素开始。
2、如果第二个元素比第一个元素小，那就交换二者位置，否则不交换，前两个元素的顺序已经固定。
3、第三个元素与前两个元素进行比较，从后向前比，先与第二个元素比，如果比第二个元素小，再与第一个元素比，比第一个元素小，就放在第一个元素的位置，第一个元素和第二个元素向后移一个位置；如果第三个元素不比第二个元素小，不交换位置，这趟的排序以固定，也就是前三个元素的大小顺序已经排好。
4、之后的排序也是这么进行。

 

代码 

function insertSort(arr) {
  var len1 = arr.length;
  for (var i = 1; i < len1; i++) {
    var now = arr[i]; // 当前趟的元素
    var lastIndex = i - 1; // 已经排好序的序列里的最后一个元素
    // 从后向前遍历已经排好序的序列
    // 如果当前趟的元素now比已经排好序的序列的元素小
    while (lastIndex >= 0 && arr[lastIndex] > now) {
      arr[lastIndex + 1] = arr[lastIndex]; // 将比now大的元素向后移一个位置
      lastIndex--;
    }
    arr[lastIndex + 1] = now; // 将当前趟的元素now插入到已经排好序的序列里
  }
  return arr;
}
 
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 12, 46, 4, 19, 50, 48];
 
console.log(insertSort(arr)); // [3,  4,  5, 12, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

桶排序 

桶排序（Bucket Sort）是一种线性排序算法，它利用了函数的映射关系，将要排序的数据分到有限数量的桶子里，每个桶子再分别排序。桶排序的时间复杂度取决于桶的数量和桶内使用的排序算法，通常情况下是O(n+k)。

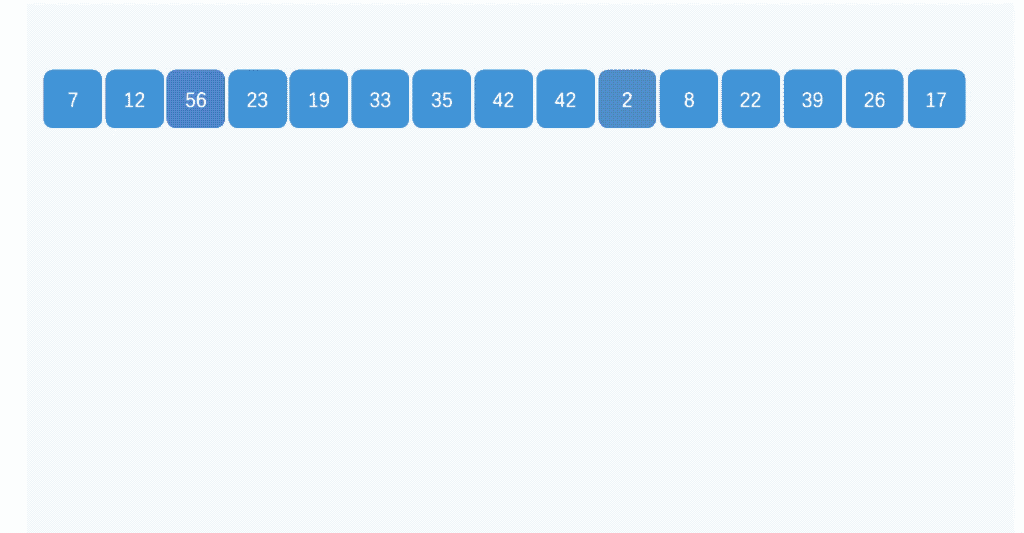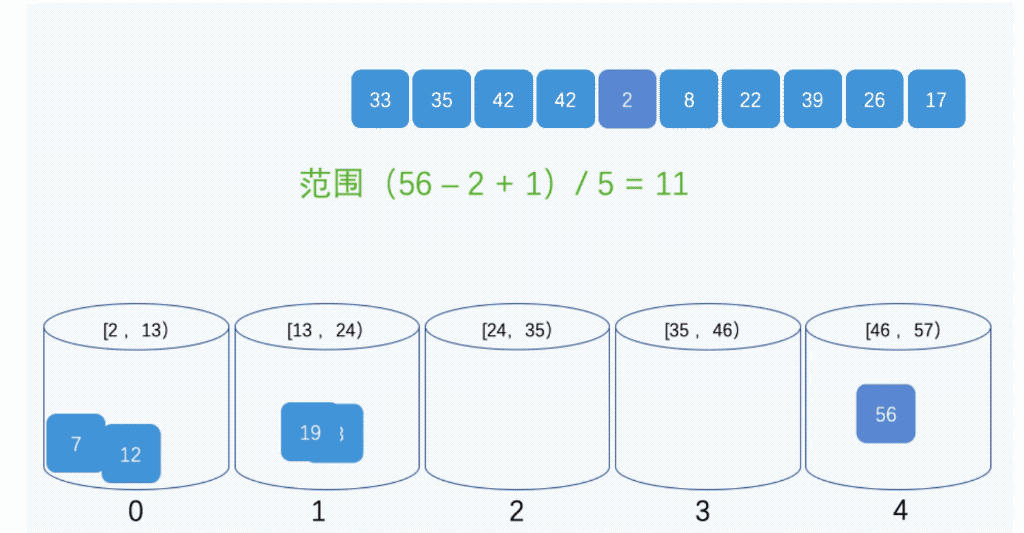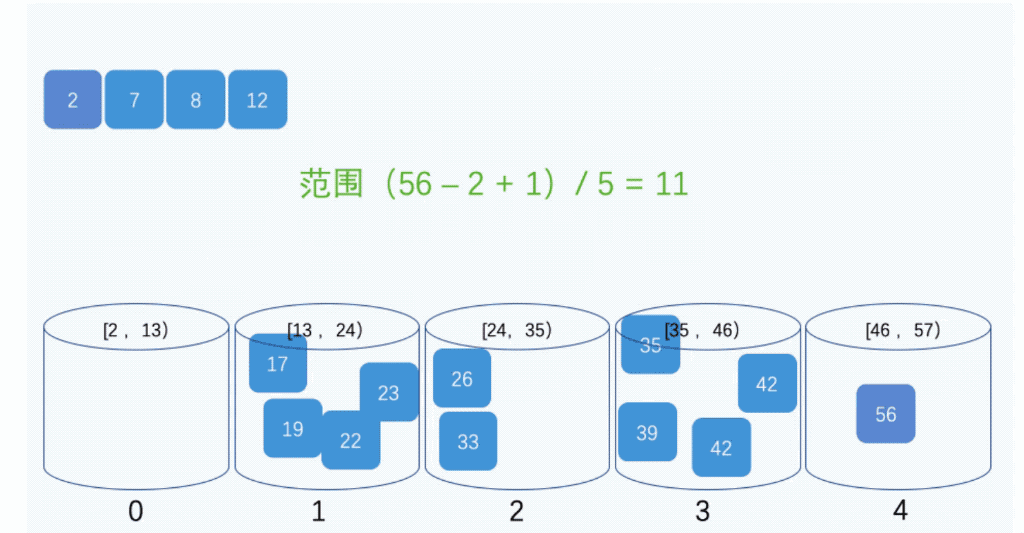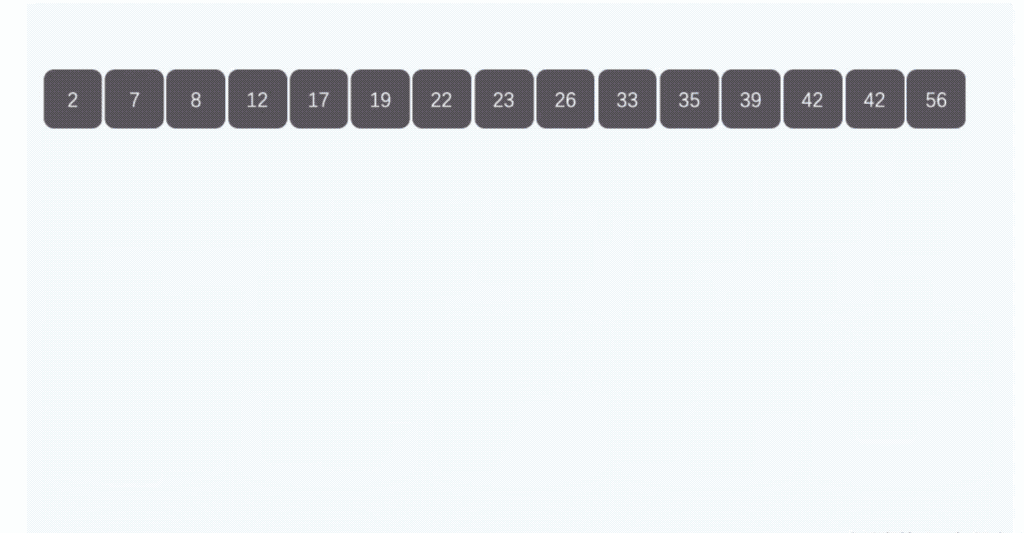
代码 

function bucketSort(arr, bucketSize) {
  if (arr.length === 0) {
    return arr;
  }
 
  var minValue = arr[0];
  var maxValue = arr[0];
  for (var i = 1; i < arr.length; i++) {
    if (arr[i] < minValue) {
      minValue = arr[i]; // 输入数据的最小值
    } else if (arr[i] > maxValue) {
      maxValue = arr[i]; // 输入数据的最大值
    }
  }
 
  // 桶的初始化
  var DEFAULT_BUCKET_SIZE = 5; // 设置桶的默认数量为5
  bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
  var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
  var buckets = newArray(bucketCount);
  for (var i = 0; i < buckets.length; i++) {
    buckets[i] = [];
  }
 
  // 利用映射函数将数据分配到各个桶中
  for (var i = 0; i < arr.length; i++) {
    buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
  }
 
  arr.length = 0;
  for (var i = 0; i < buckets.length; i++) {
    insertionSort(buckets[i]); // 对每个桶进行排序，这里使用了插入排序
    for (var j = 0; j < buckets[i].length; j++) {
      arr.push(buckets[i][j]);
    }
  }
 
  return arr;
}

基数排序

基数排序（Radix Sort）是一种多关键字排序算法，可用于对数字序列进行排序。基数排序先按照最低有效位（LSB）对元素进行排序，然后依次按照次低有效位、次次低有效位……最高有效位进行排序。该算法的时间复杂度为O(d*(n+k))，其中d表示数字位数，k表示每个数字可能的取值范围。

代码 

var counter = [];
function radixSort(arr, maxDigit) {
  var mod = 10;
  var dev = 1;
  for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
    for (var j = 0; j < arr.length; j++) {
      var bucket = parseInt((arr[j] % mod) / dev);
      if (counter[bucket] == null) {
        counter[bucket] = [];
      }
      counter[bucket].push(arr[j]);
    }
    var pos = 0;
    for (var j = 0; j < counter.length; j++) {
      var value = null;
      if (counter[j] != null) {
        while ((value = counter[j].shift()) != null) {
          arr[pos++] = value;
        }
      }
    }
  }
  return arr;
}