Map 和 Set-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_62921710/article/details/131041982

本文介绍了二叉搜索树的基本概念，包括其定义和特性。详细阐述了如何进行查找、插入和删除操作。查找操作通过比较节点值来定位；插入操作将新节点插入到正确位置，保持树的有序性；删除操作则要考虑多种情况，如删除节点的子节点为空或非空的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.二叉搜索树

概念：又称二叉排序树，它或是一棵空树，或者是具有以下性质的二叉树：

（1）.若左子树不为空，那么它的左子树上的节点值都小于根节点的值；

（2）.若右子树不为空，那么它的右子树上的节点值都大于根节点的值；

（3）.他的左右子树仍为搜素二叉树；

2.二叉搜索树的查找

public TreeNode root;//根节点
    public  TreeNode searchVal(int key)
    {
        TreeNode cur=root;
       while(cur!=null)
       {
           if(cur.val>key)
           {
               cur=cur.left;
           }
           else if(cur.val<key)
           {
               cur=cur.right;
           }
           else if (cur.val==key)
           {
               return cur;
           }
       }
        return null;
    }

3.二叉搜索树的插入

思路：

//二叉搜索树再插入数据的时候一定插入到叶子位置
//parent=cur;
//cur=cur.nxet;找到后判断该叶子节点值无key的大小，在选择要插入的位置，若要插入的数字已经在二叉搜索树内，则无法插入

public boolean insert(int key)
    {
        TreeNode node=new TreeNode(key);
        if(root==null)
        {
           root=node;
           return true;
        }
        TreeNode cur=root;
        TreeNode parent=cur;
        while(cur!=null)
        {
            if(cur.val<key)
            {
                parent=cur;
                cur=cur.right;
            }else if (cur.val==key)
            {
                return false;
            }
            else if(cur.val>key)
            {
                parent=cur;
                cur=cur.left;
            }
        }
        if(parent.val>key)
        {
            parent.left=node;
        }
        else
        {
            parent.right=node;
        }
        return true;
    }

4.二叉树的元素删除

思路：（1）找到要删除的节点在不在二叉树中

设待删除的节点是cur，待删除的节点的双亲节点是parent

1cur.left==null

1.1cur是root 则root=cur.right;

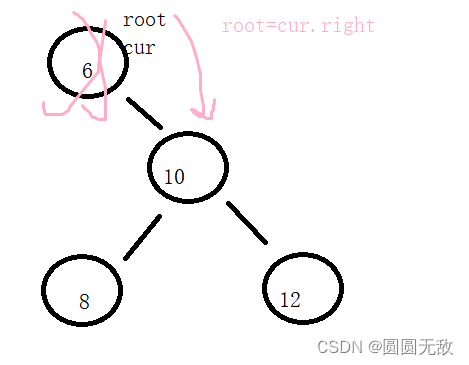
1.2cur不是root，cur是parent.left;

1.3cur不是root，cur是parent.right

2.cur.right==null

2.1cur=root则root=cur.left;

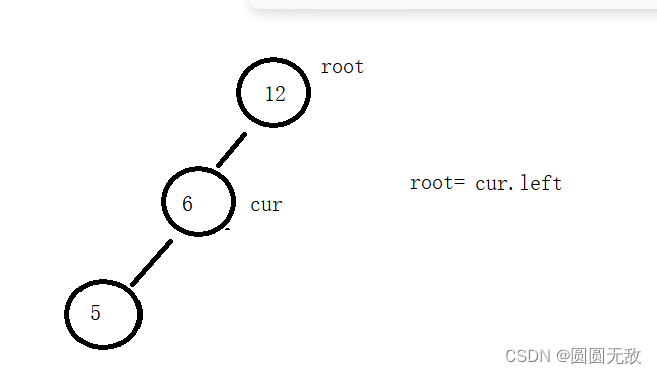
2.2cur不是root，cur是parent.left;

2.3 cur不是root，cur 是parent .right;

cur.left和cur.right 都不为kong（替罪羊删除法）

 public void removeNode(int key)
    {
        if(root==null)
        {
            return;
        }
        TreeNode cur=root;
        TreeNode parent=root;
        while(cur!=null)
        {
            if(cur.val>key)
            {
                parent=cur;
                cur=cur.left;
            }
            else if (cur.val<key) {
               parent=cur;
               cur=cur.right;
            }
            else if(cur.val==key)
            {
                remove(cur,parent);
            }
        }
    }
    public void remove(TreeNode cur,TreeNode parent)
    {
        if(cur.left==null)
        {
            if(cur==root)
            {
                root=cur.right;
            } else if (cur == parent.left) {
                parent.left=cur.left;
            }
            else if(cur==parent.right)
            {
                parent.right=cur.right;
            }
        }
        else if (cur.right==null)
        {
            if(cur==root)
            {
                root=cur.left;
            }
            else if(cur==parent.left)
            {
                parent.left=cur.left;
            } else if (cur==parent.right) {
                parent.right=cur.left;

            }
        }
        else
        {
            TreeNode tp=cur;
            TreeNode t=cur.right;
            while(t!=null)
            {
                tp=t;
                t=t.left;
            }
            cur.val=t.val;
            if(t==tp.left) {
                tp.left = t.right;
            }
            else
            {
                tp.right=t.right;
            }
    }