一、题目描述
给你一个正整数 n ,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
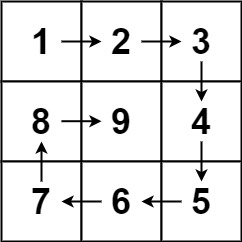
输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
二、解题思路
- 初始化一个 n x n 的矩阵,所有元素设为 0。
- 定义一个变量
value用来填充矩阵,起始值为 1。 - 使用四个变量
startRow,endRow,startCol,endCol来标记当前填充区域的边界。 - 在一个循环中,按照螺旋顺序填充矩阵,每次填充完一层后,边界向内收缩,直到所有元素都被填充。
- 填充顺序为:从左到右,从上到下,从右到左,从下到上,每次填充后更新边界。
三、具体代码
class Solution {
public int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
int value = 1;
int startRow = 0, endRow = n - 1;
int startCol = 0, endCol = n - 1;
while (value <= n * n) {
for (int i = startCol; i <= endCol; i++) {
matrix[startRow][i] = value++;
}
startRow++;
for (int i = startRow; i <= endRow; i++) {
matrix[i][endCol] = value++;
}
endCol--;
if (startRow <= endRow) {
for (int i = endCol; i >= startCol; i--) {
matrix[endRow][i] = value++;
}
endRow--;
}
if (startCol <= endCol) {
for (int i = endRow; i >= startRow; i--) {
matrix[i][startCol] = value++;
}
startCol++;
}
}
return matrix;
}
}四、时间复杂度和空间复杂度
1. 时间复杂度
- 该算法的主要操作是按螺旋顺序填充矩阵。每次循环迭代都会填充一层,直到所有
n * n个元素都被填充完毕。 - 每层包含的元素数量从
n开始递减,直到 1。具体来说,第一层有n个元素,第二层有n - 2个元素,依此类推,直到最后一层只有 1 个元素。 - 因此,总的元素数量是
n * (n + 1) / 2,这是一个等差数列的求和公式。 - 所以,时间复杂度为 O(n^2),因为我们需要填充整个 n x n 矩阵。
2. 空间复杂度
- 空间复杂度主要由创建的 n x n 矩阵决定,因为这是算法中唯一的额外空间消耗。
- 矩阵占用的空间是
n * n * int.size,其中int.size是整型变量在内存中的大小(通常为 4 或 8 字节)。 - 因此,空间复杂度为 O(n^2)。
五、总结知识点
1. 二维数组的初始化和使用:代码中创建了一个 n x n 的二维数组 matrix 用于存储生成的螺旋矩阵。
2. 循环控制:使用 while 循环来控制矩阵填充的过程,循环条件是 value(当前填充的数值)是否超过了矩阵元素的总数 n * n。
3. 变量的使用:
value用于记录当前应该填充的数值。startRow和endRow表示当前填充区域的行的起始和结束索引。startCol和endCol表示当前填充区域的列的起始和结束索引。
4. 螺旋填充逻辑:代码通过四个方向的循环来填充矩阵,每个方向填充后,都会更新 value 和边界索引 startRow, endRow, startCol, endCol。这四个方向分别是:
- 从左到右填充顶层。
- 从上到下填充右侧。
- 从右到左填充底层。
- 从下到上填充左侧。
5. 边界更新:在每次填充完一个方向后,需要根据当前的填充位置和矩阵的边界来更新 startRow, endRow, startCol, endCol 的值,以便下一次循环能够正确填充下一个区域。
6. 条件判断:代码中使用了 if 语句来判断是否需要改变填充方向,这是为了确保在填充过程中不会出现数组越界的错误。
7. 数值递增:在填充过程中,value 被递增,以确保每个元素的值都是唯一的。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










