[C++]背包问题（2）：洛谷榨取kkksc03&&Cow Frisbee Team S 更多约束条件下的01背包

这篇博客介绍了两种基于动态规划的解题策略，分别是01背包问题的拓展和存在倍数约束条件的情况。在01背包问题中，通过二维动态规划解决两个最大值约束条件的问题。而在倍数约束条件下，通过取余和状态转移方程求解方案个数，并使用滚动数组优化存储空间。博客提供了详细的解题思路和代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

还不熟悉01背包的同学可以先看一下上一期的题解：

[C++]背包问题（1）：洛谷采药 01背包模型详解

-01背包拓维-

[原题]

榨取kkksc03

[输入样例]

[输出样例]

[解题思路]

不难看出，这道题是01背包模型的拓展。在上一次的题解中，我们要求从M个物品中选择T时间内最大的价值组合，而∑(items[k].time)<=T则是模型的最大值约束条件（k表示每一个被选择的物品）。

而这道题最大的不同之处在于，存在两个最大值约束条件M和T（注意此处的M与上一题的M含义不同），而且他们的地位是相同的。因此，我们可以用相同的方式去处理他们。

对于单一的约束条件T，我们有

dp[j] = max(dp[j], dp[j - item[i].t] + item[i].val)

那么，对于两个约束条件T和M（显然，由于条件的增多，我们的dp数组也需要对应地升维），我们可以类比得到

dp[i][j] = max(dp[i][j], dp[j - item[i].t][j - item[i].m] + item[i].val)

当然，这道题中并没有给每一个愿望赋予特殊的价值，只需要统计对应的个数，因此这里的item[i].val即为1。

接下来，让我们看一下整道题的代码：

#include<iostream>
#include<vector>
using namespace std;

class Wish
{
public:
	int money;
	int time;

	Wish(int m = 0,int t = 0):money(m),time(t){}
};

int main()
{
	int n, M, T;
	cin >> n >> M >> T;
	vector<Wish> arr(n);
	for (int i = 0; i < n; i++)
	{
		int m, t;
		cin >> m >> t;
		arr[i] = Wish(m, t);
	}
	vector<vector<int>> dp(M + 1, vector<int>(T + 1, 0));

	for (int i = 0; i < n; i++)
	{
		for (int j = M; j >= arr[i].money; j--)
		{
			for (int k = T; k>= arr[i].time; k--)
			{
				dp[j][k] = max(dp[j][k], dp[j - arr[i].money][k - arr[i].time] + 1);
			}
		}
	}

	cout << dp.back().back();
	return 0;
}

-特殊的约束条件：倍数-

[原题]

[输入样例]

[输出样例]

[解题思路]

与常规的01背包模型不同的是，这道题给出的约束条件并非最大值，而是要求和为F倍数的方案个数。而倍数问题，我们自然而然就会想到取余。

接下来，我们就通过列表的方式来研究一下余数（我们用j来表示）和物品组合（我们用i来表示）之间，能否找到一个合适的状态转移方程。（以下数据皆取自题目样例）

我们首先建立如下表格，并完成第一行的填写：

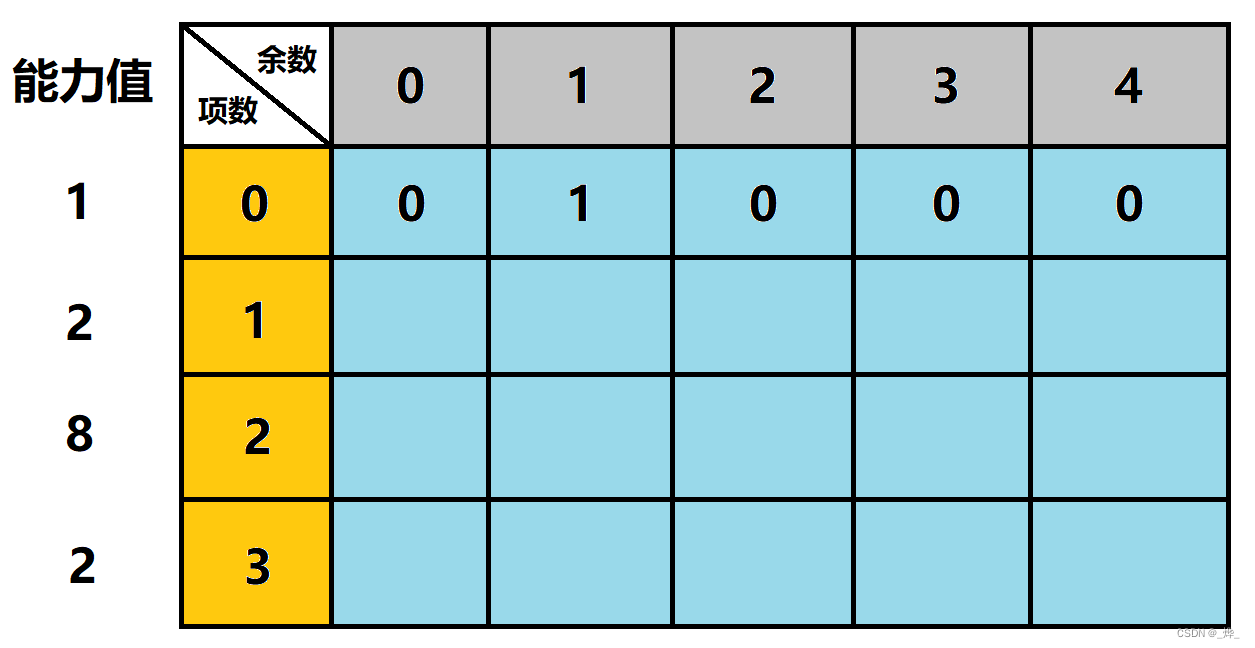
接下来是第二行：

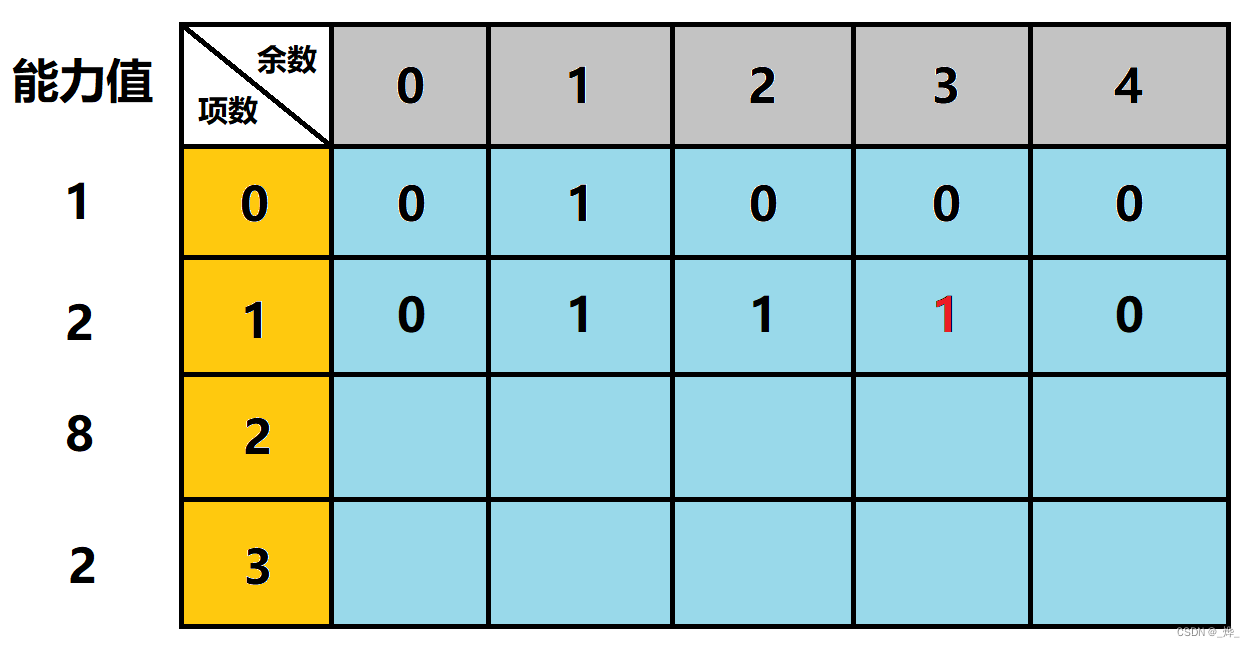
我们来对这一行产生的三个1作一下简单的分析：

（1）对于j==1处的1，显然是由上一行的结果直接继承下来的；

（2）对于j==2处的1，则是由本身2%F得到余数2产生的可行方案；

（3）而对于j==3处，则是由于(1+2)%F得到余数3产生的方案，但是我们仍然难以找到一个固定的式子去表示这种关系，在这里，我们用红色将其标注了出来。

对于第三、第四行，我们仍然采用这样的方式去完成，为了更清楚地反映结果，我们用黑色、绿色、红色分别将上述（1）、（2）、（3）相同方式产生的方案标注出来，结果如下：

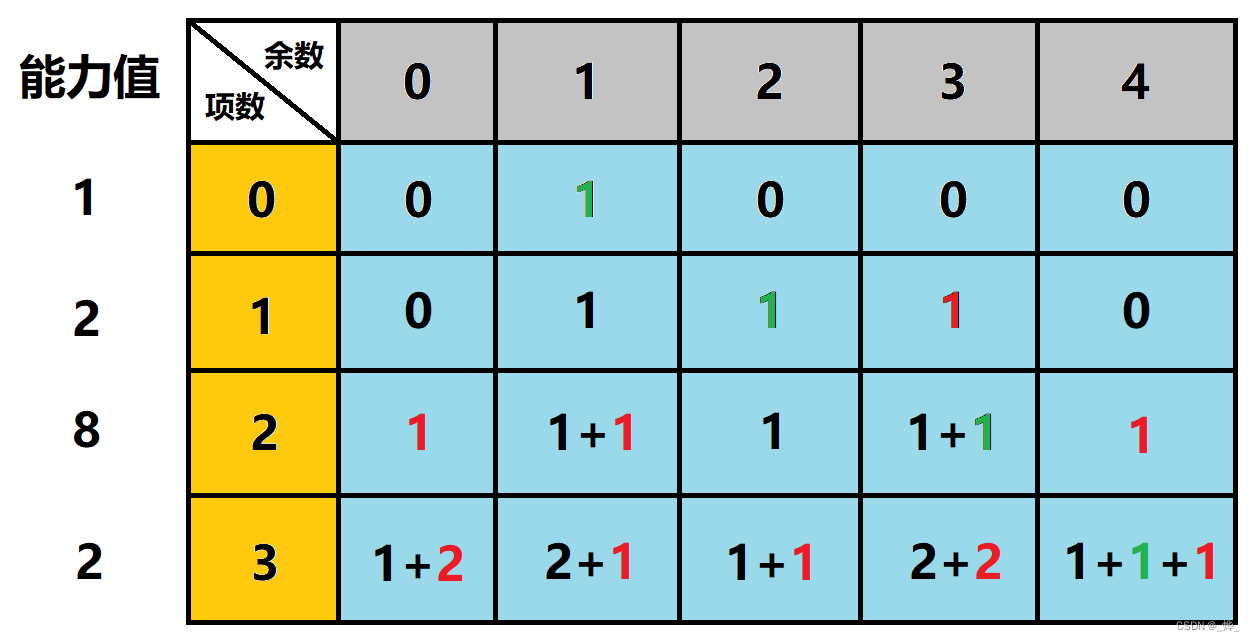
显然，每一格的结果都是由三个部分决定的，而这三个部分恰好是上述（1）（2）（3）对应的三种情形。由于情形（3）比较复杂，我们这里将其单独拿出来讨论一下。

对于第二行的情形（3）我们是如何得到的？我们由等式(1+2)%F==j（此处F=5,j=3）作出了“此方案可行”的判断。当然，我们可以对这个等式进行适当的变形，即：

1==(j-2+F)%F（先加上F再取余是为了防止j-2为负数）

如果这是个重要的关系式，那么等式左边的1又该如何解释呢？让我们将目光移向上一行：j=1处的值恰好就是转移到这一格的值。那么，这第三部分的值我们也可以用通式表示出来了：

V = dp[i - 1][(j - arr[i] + F) % F]

最终，我们可以得到这样一个状态转移方程：

dp[i][j] = (dp[i - 1][j]) + (arr[i] == j ? 1 : 0) + (dp[i - 1][(j - arr[i] + F) % F])

为了防止数字越界，优化存储空间，我们还可以进行一些处理：

*一个简单的预处理

由于我们只对n%F的余数进行操作，因此我们可以在数字读取阶段就将每一项%F后储存。

*对每一项计算都执行取模运算

由于题目要求结果对10^8取模，我们可以让dp的每一项都对10^8取模后再相加，因为(a+c)%b==(a%b+c%b)%b是个恒等式。

*滚动数组

由于dp的每一项结果只与本行和上一行结果有关，因此我们可以将二维数组优化为两个一维数组，具体原理已经在上一个题解中详细解释过。

最后，让我们直接来看代码吧：

#include<iostream>
#include<vector>
using namespace std;

int main()
{
	//数据读取及数组声明
	const int mod = 1e8;
	int N, F;
	cin >> N >> F;
	vector<int> arr(N);
	for (int i = 0; i < N; i++)
	{
		int n;
		cin >> n;
		arr[i] = n % F;//直接取余后存储
	}
	vector<int> first(F, 0);
	vector<int> second(F, 0);

	for (int i = 0; i < N; i++)
	{
		first = second;//将second的数据覆盖first的无用数据
		for (int j = 0; j < F; j++)
		{
			second[j] = (((arr[i] == j ? 1 : 0) + (first[j])) % mod + (first[(j - arr[i] + F) % F]) % mod) % mod;//对每一个都%mod
		}
	}

	//注意我们要求的是“倍数”，因此应返回取余后余数为0的结果
	cout << second[0];
	return 0;
}