[C++]LeetCode 地图分析 解题思路及详解

[原题]

你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

[示例]

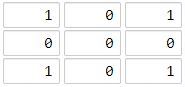
示例一
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

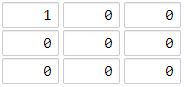
示例二
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

[解题思路]

给我们一张网格图，用0和1分别表示海洋和陆地，要求海洋与离它最近的陆地距离的最大值，此处，距离为两个单元格的横坐标之差与纵坐标之差的和。

由于所求为海洋与最近的陆地单元格距离，我们不妨以每个陆地单元格为中心点向外搜索，并为每个海洋单元格赋上距离的权值，再取其最大值，即可得到最终的答案。这种方法，就是广度优先搜索（BFS）。

对于一张图的搜索，我们通常采用深度优先搜索（DFS）和广度优先搜索（BFS）两种方式。DFS，即以某一单元格为起点，每次选取临近的某一单元格进行访问，最终通过一条路径到达终点单元格。然后，不断通过回溯来完成对所有单元格的访问。

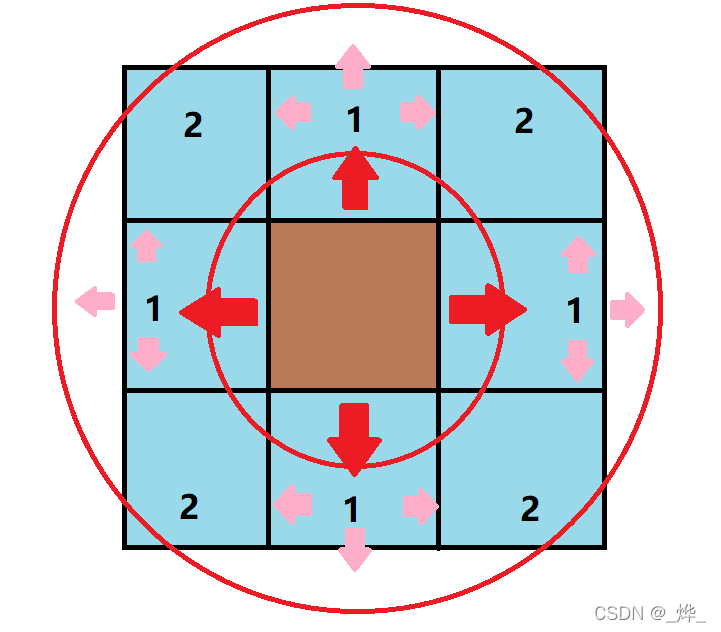
与DFS不同的是，BFS是以某一单元格为中心，每次访问所有临近的单元格，然后依次扩大访问的范围，直到完成对所有单元格的访问。对于这一过程，可以用如下示意图来演示：

那么，我们该如何实现BFS呢？与二叉树的层序遍历类似，我们需要借助一个特殊的容器——队列。接下来，我们来模拟一下如下图单源BFS的实现：

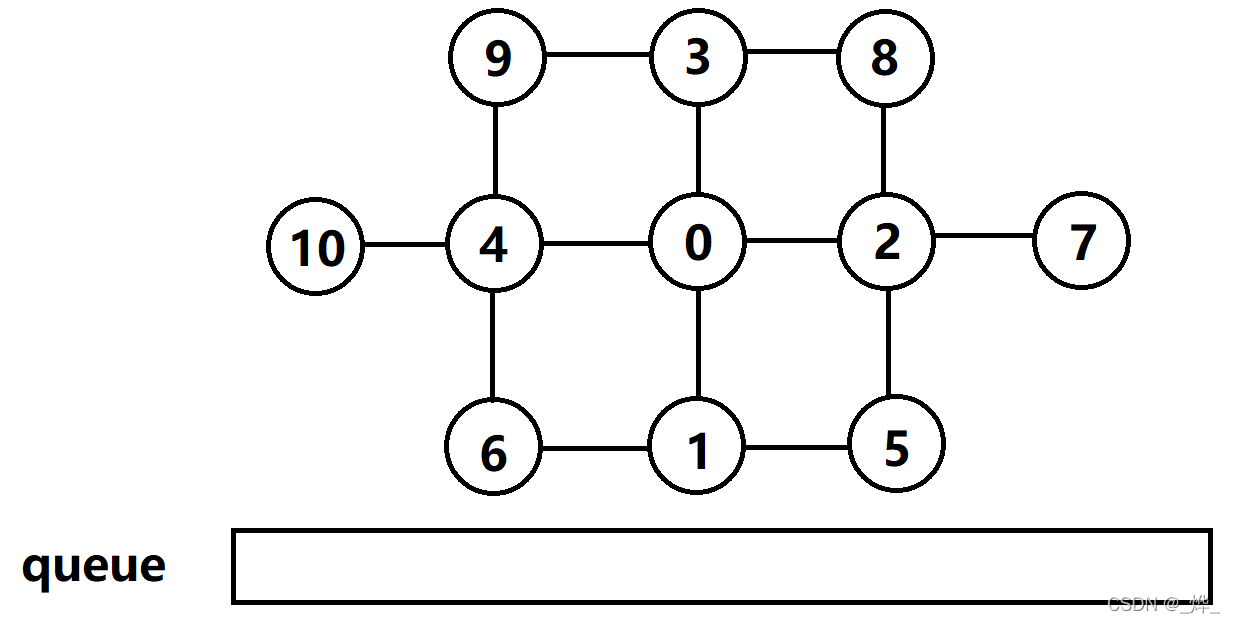
（1）源节点0入队；

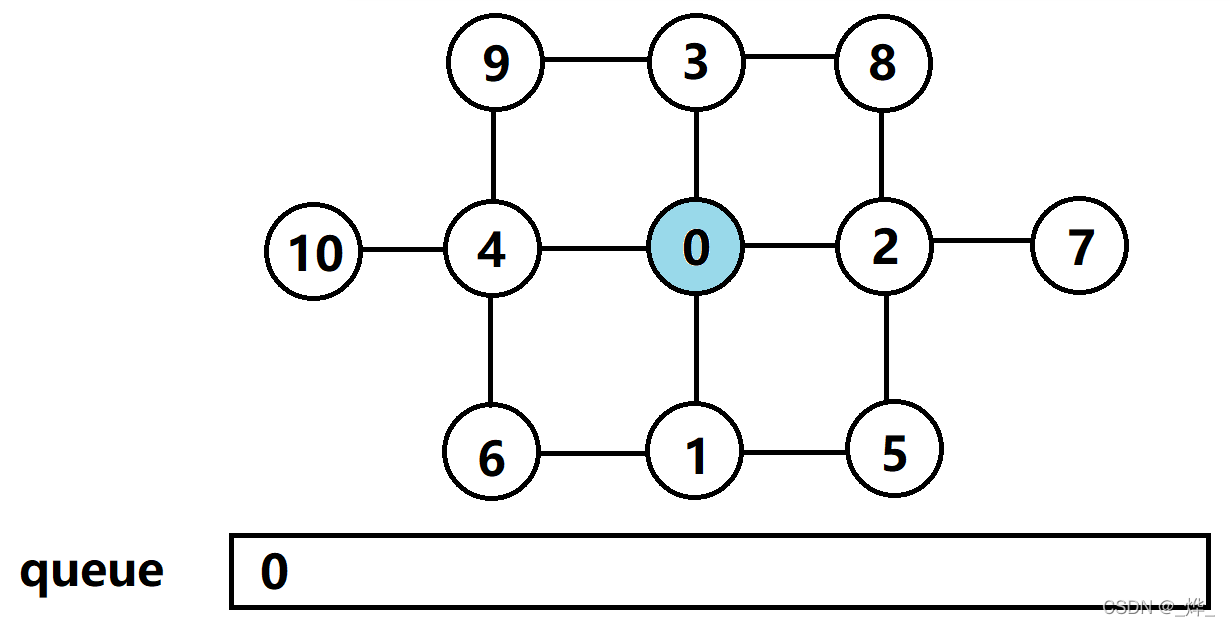
（2）节点0的相邻节点1、2、3、4入队，源节点0出队；

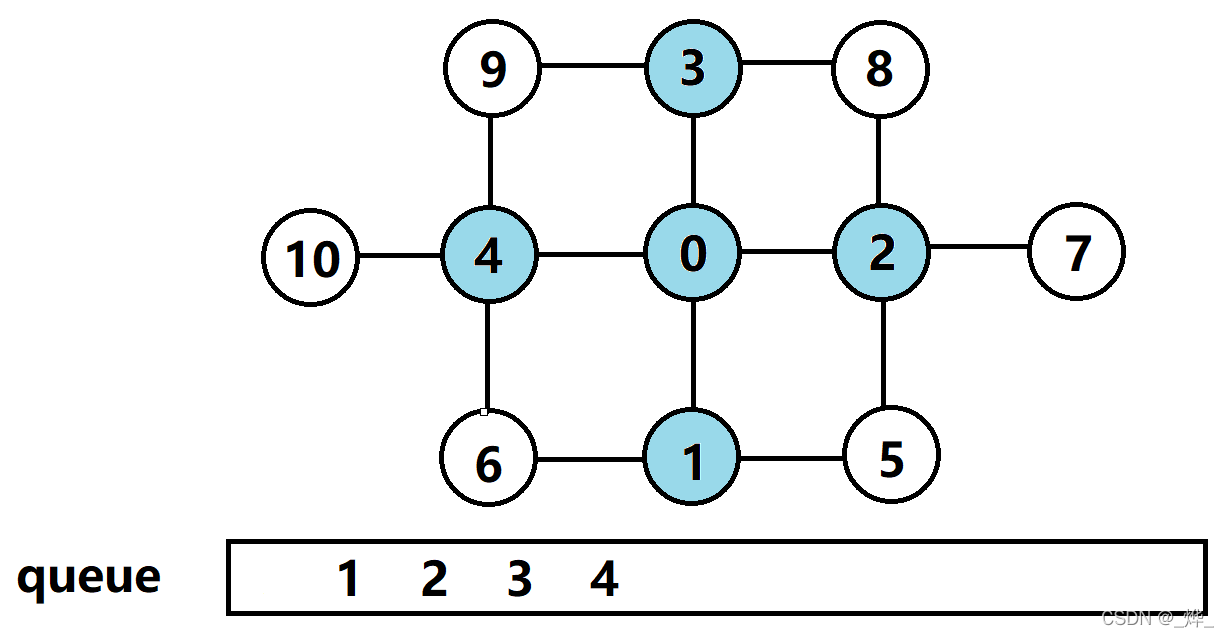
（3）节点1的相邻节点5、6入队，节点1出队；

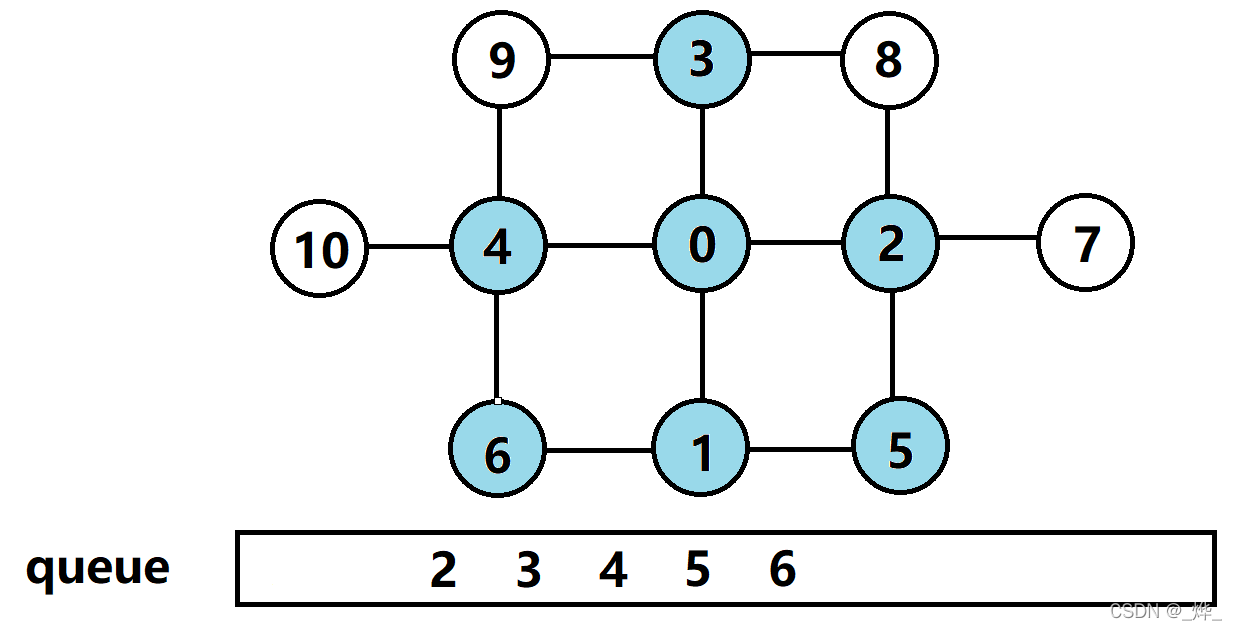
（4）节点2的相邻节点7、8入队，节点2出队；

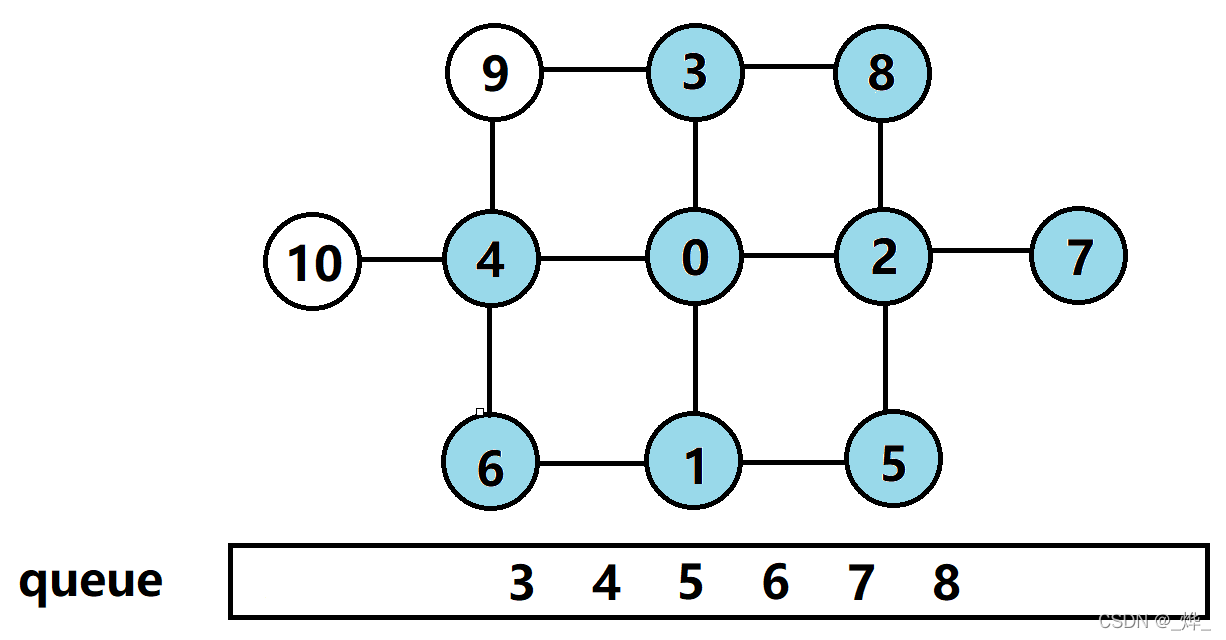
（5）节点3的相邻节点9、10入队，节点3出队；

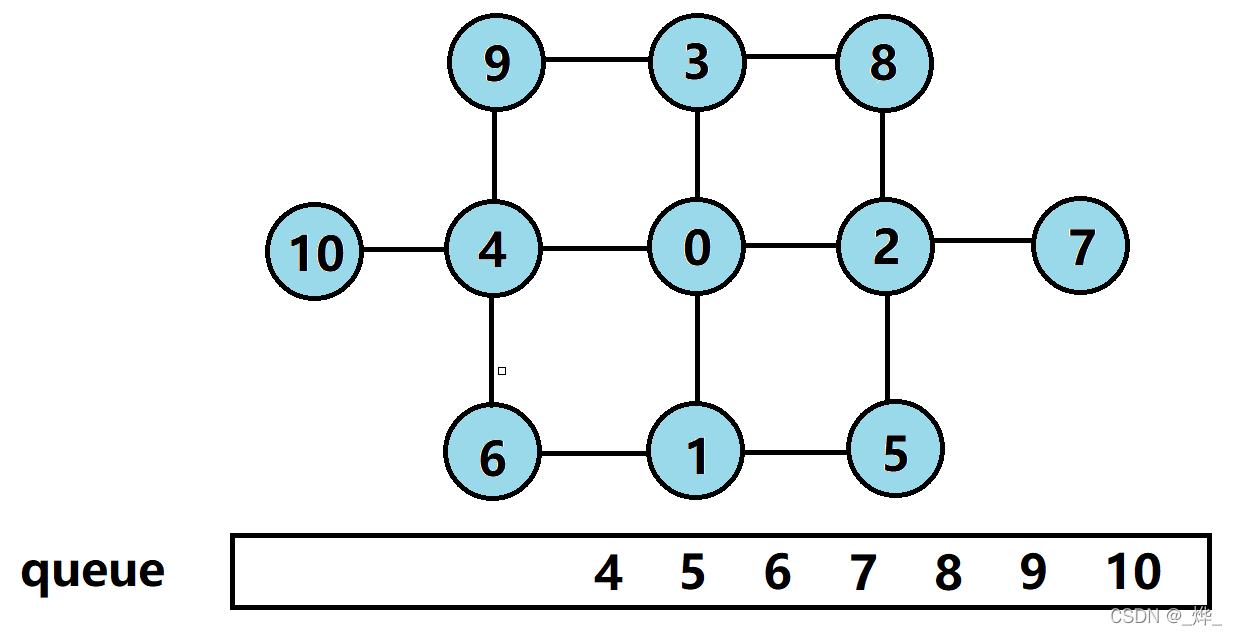
（6）队列中剩余节点都无未访问过的相邻节点，依次出队，结束BFS。

当然，本题中并不是一个单源的BFS，而是从每个陆地节点出发的多源BFS，因此，我们需要统计每个陆地节点的位置，并在（1）步骤中将每个陆地节点入队，其他过程与上述过程相类似。

现在，我们已经确定了搜索的方式，我们又该如何算出每个海洋单元格最近的陆地的距离呢？对于一个有向图的最短路径问题，我们通常有迪杰斯特拉（Dijkstra）算法和弗洛伊德（Floyd）算法两种方式。这里，我们将使用迪杰斯特拉算法。

在一个有向图中，首先从起点开始，访问所有临近的节点，并更新每个节点的权值（若大于原有数值则不更新），直到所有临近节点都被访问过后，选择一个已找到最短路径且权值最小的节点作为下一个起点，重复上述过程。因此，对于每个节点，我们需要一个visited数组来存放是否已取到最短路径（或不存在入度），及一个distance数组来存放源点到每个节点距离的最小值。

让我们用下图的例子来演示一下Dijkstra算法求S节点到所有节点最短路径的过程：

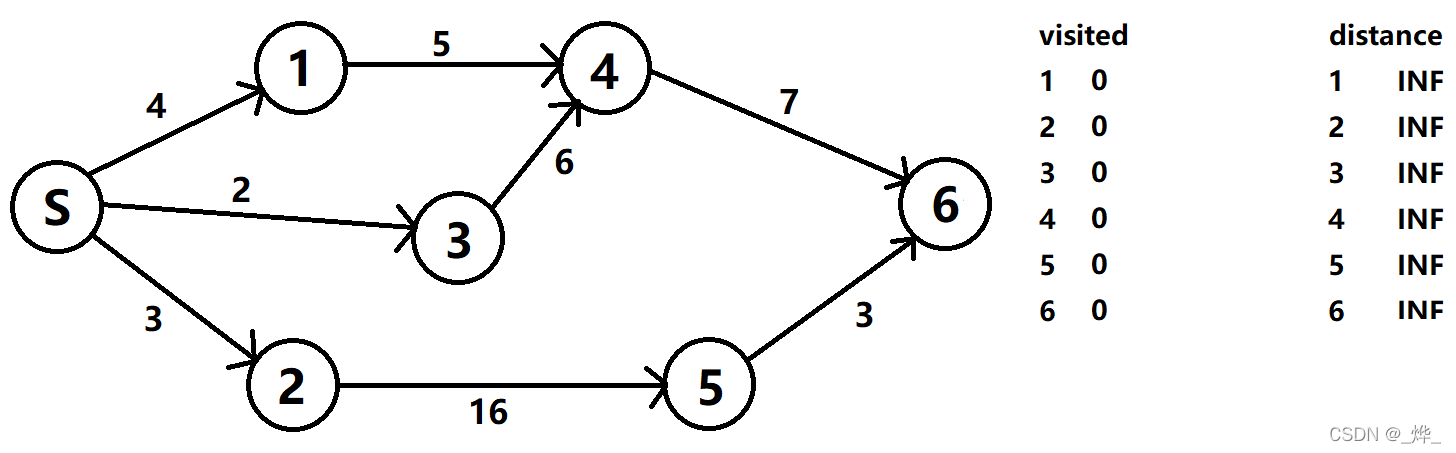
（1）首先从S节点出发，依次访问节点1、2、3，并更新数值。此时1、2、3都没有入度了，visited数组更新为1。

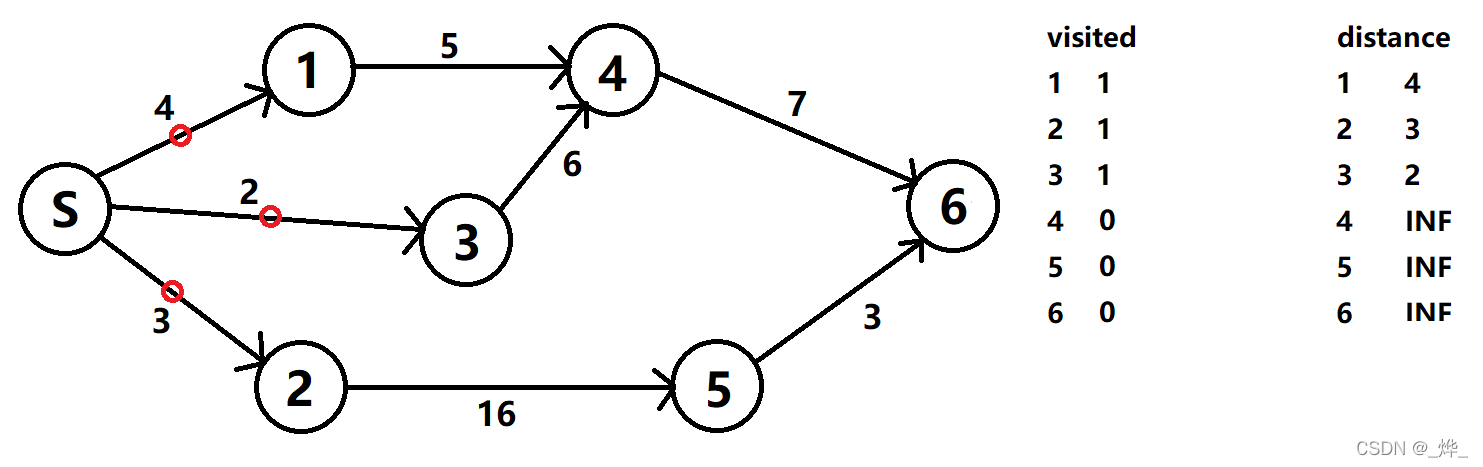
（2）从visited为1且权值最小的3节点开始，访问4节点并更新数值。

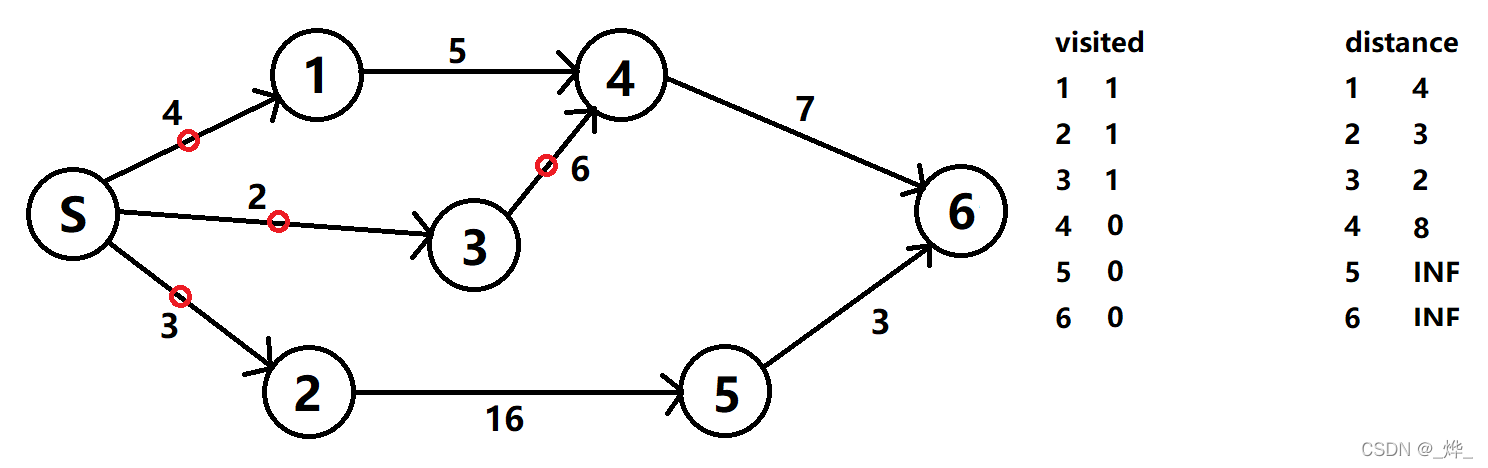
（3）从visited为1且权值次小的2节点开始，访问5节点并更新数值。此时5节点没有入度，更新visited数组。

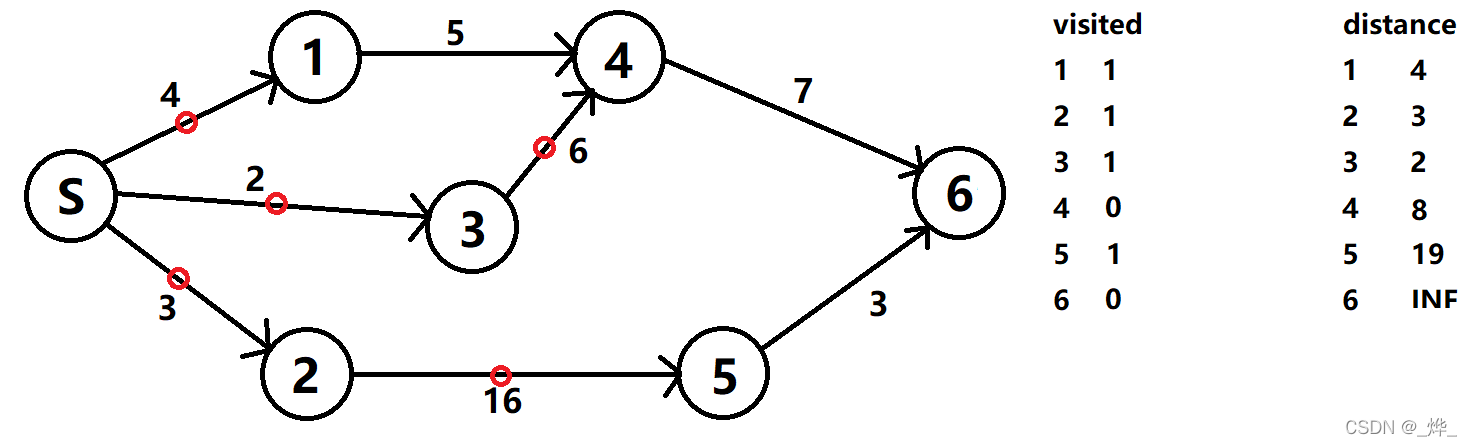
（4）从节点1开始，访问4节点，由于4+5>8，不更新节点。此时4节点没有入度，更新visited数组。

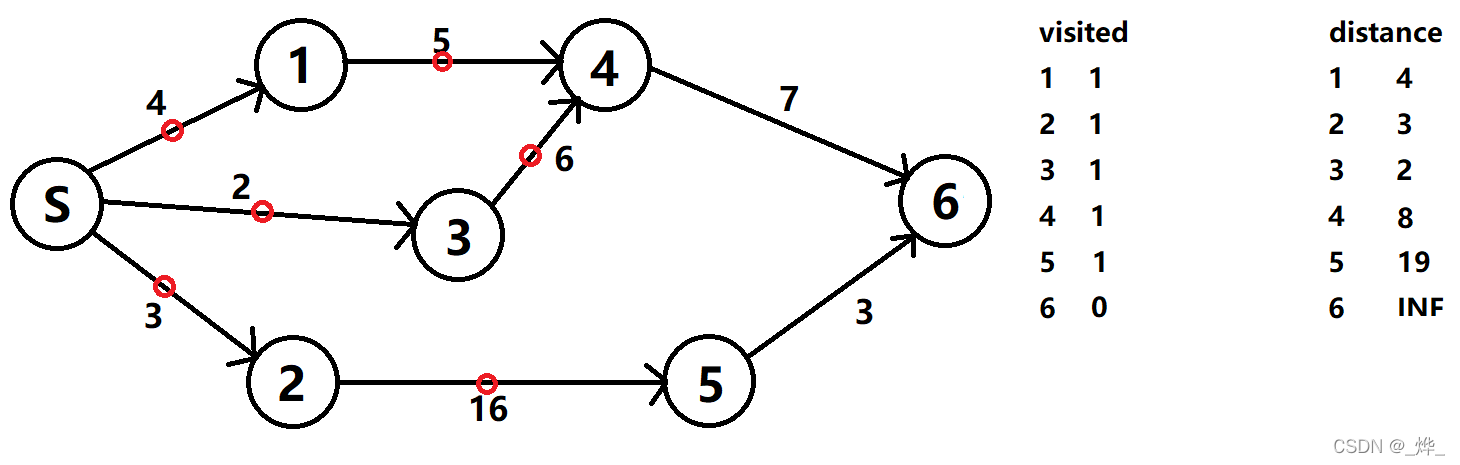
（5）由于4节点的权值小于5节点，我们以4节点为起点，访问6节点并更新数值。所有节点已取得路径最小值，结束遍历。

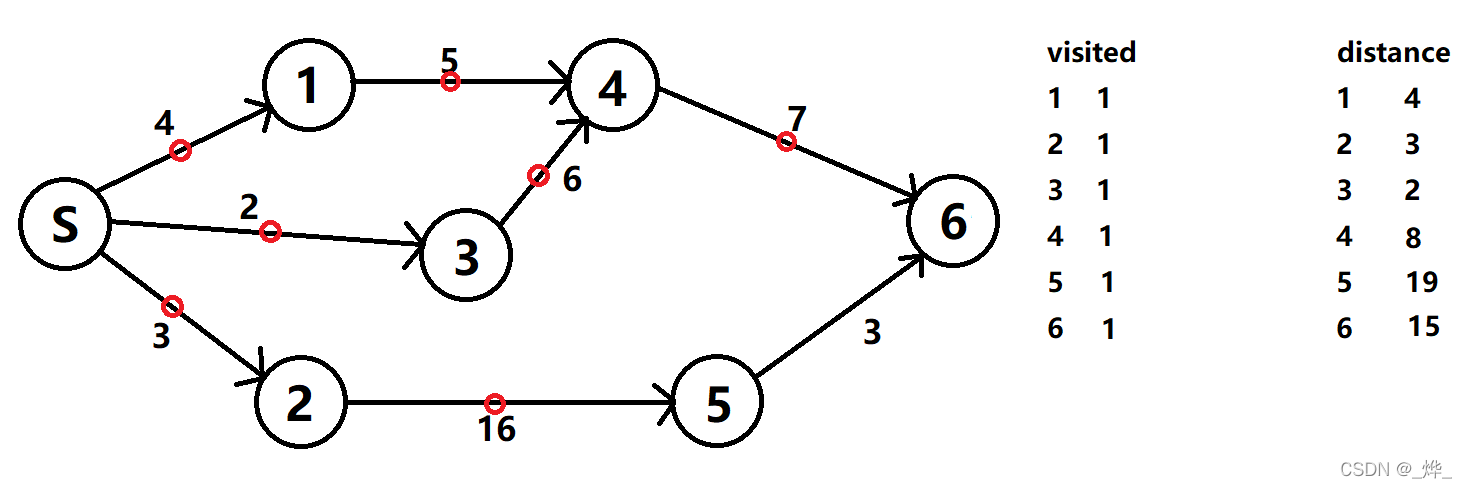
本题则是对Dijkstra的变形，从多个源点出发，寻找每个单元格的最短路径，且每条边权值都为1。而对于上述的distance数组，我们不妨直接将距离记录在grid数组中，即每次进行BFS时，都将该海洋单元格的数据记录为上一个单元格数据+1。而对于visited数组，我们可以直接判断该海洋单元格是否为0：由于我们的搜索顺序是各个源点顺次交替进行BFS，因此单元格越早更新，所取到的权值越小，所以我们认为，当一个单元格得到更新，则已经取到了最短路径，即已被访问结束，后续不再进行访问。因此当某个海洋单元格为0时，它一定没有被访问结束；当某个海洋单元格不为0时，它一定完成了访问。

另外，由于陆地单元格初值便为1，每个单元格最后所得的距离实际上多算了1，因此返回的最大值也应减去1。

接下来，让我们来看一下整道题的代码（一些细节以批注形式呈现）：

//由于队列中需要存储每个单元格的数据，我们不妨定义一个点类来方便存储单元格的横坐标、纵坐标
class Points
{
public:
    int x;
    int y;

    //构造函数
    Points(int _x, int _y) :x(_x), y(_y) {}
};

class Solution
{
public:
    int maxDistance(vector<vector<int>>& grid) {
        int maxDistance = -1;//存放距离的最大值

        //定义dx和dy来分别对应上下左右四个搜索方向
        int dx[4] = { 1,0,-1,0 }, dy[4] = { 0,1,0,-1 };

        //队列的声明，模板类型为刚才定义的Points类
        queue<Points> q;

        //遍历搜索陆地单元格，并放入队列中
        for (int i = 0; i < grid.size(); i++)
        {
            for (int j = 0; j < grid[0].size(); j++)
            {
                if (grid[i][j] == 1)
                    q.push(Points(i, j));
            }
        }

        while (!q.empty())
        {
            //分别取出队首数据的xy坐标
            int x0 = q.front().x, y0 = q.front().y;

            //向四个方向进行搜索
            for (int i = 0; i < 4; i++)
            {
                if (x0 + dx[i] >= 0 && x0 + dx[i] < grid.size() && y0 + dy[i] >= 0 && y0 + dy[i] < grid[0].size() && grid[x0 + dx[i]][y0 + dy[i]] == 0)//越界判断及是否为海洋的判断
                {
                    //更新距离和最大值
                    grid[x0 + dx[i]][y0 + dy[i]] = grid[x0][y0] + 1;
                    maxDistance = max(maxDistance, grid[x0 + dx[i]][y0 + dy[i]]);

                    //将临近节点存入队列
                    q.push(Points(x0 + dx[i], y0 + dy[i]));
                }
            }

            //弹出队首
            q.pop();
        }

        //当全是海洋时，最大值为0，当全是陆地时或只有一个单元格时，最大值为-1，按题目要求返回-1
        if (maxDistance <= 1) return -1;

        //返回最大值
        return maxDistance - 1;
    }
};