数据结构（c语言 第二版 严蔚敏）第七章 查找 期末速成版

折半查找

折半查找的课本代码如下所示

int Search_Bin(SSTable ST,ElemType key)

{

    int low=1,high=ST.length;

    while(low<=high)

    {

        mid=(low+high)/2;

        if(key==ST.R[mid].key) return mid;

        else if(key<ST.R[mid].key)   high=mid-1;

        else low=mid+1;

    }

    return 0;

}

折半查找的循环条件是low<=high，如果出现了low=high还要再进行一次循环体内的代码。Mid=（low+high）/2 然后high=mid-1，这时候low就大于high了。函数就会跳出循环体了。

折半查找可以用二叉树来表示，把当前查找区间的中间位置作为根，左子表和右子表作为根的左子树和右子树。    

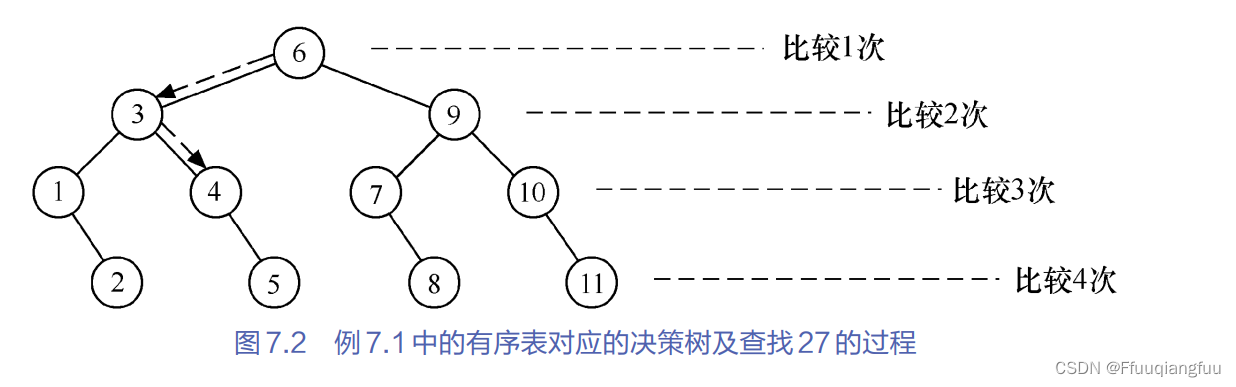
折半查找在查找成功的时候比较的关键字的个数最多不超过树的深度。决策树的形态也只跟n的个数有关，决策树的深度为log2n(以2为底n的对数向下取整)+1。

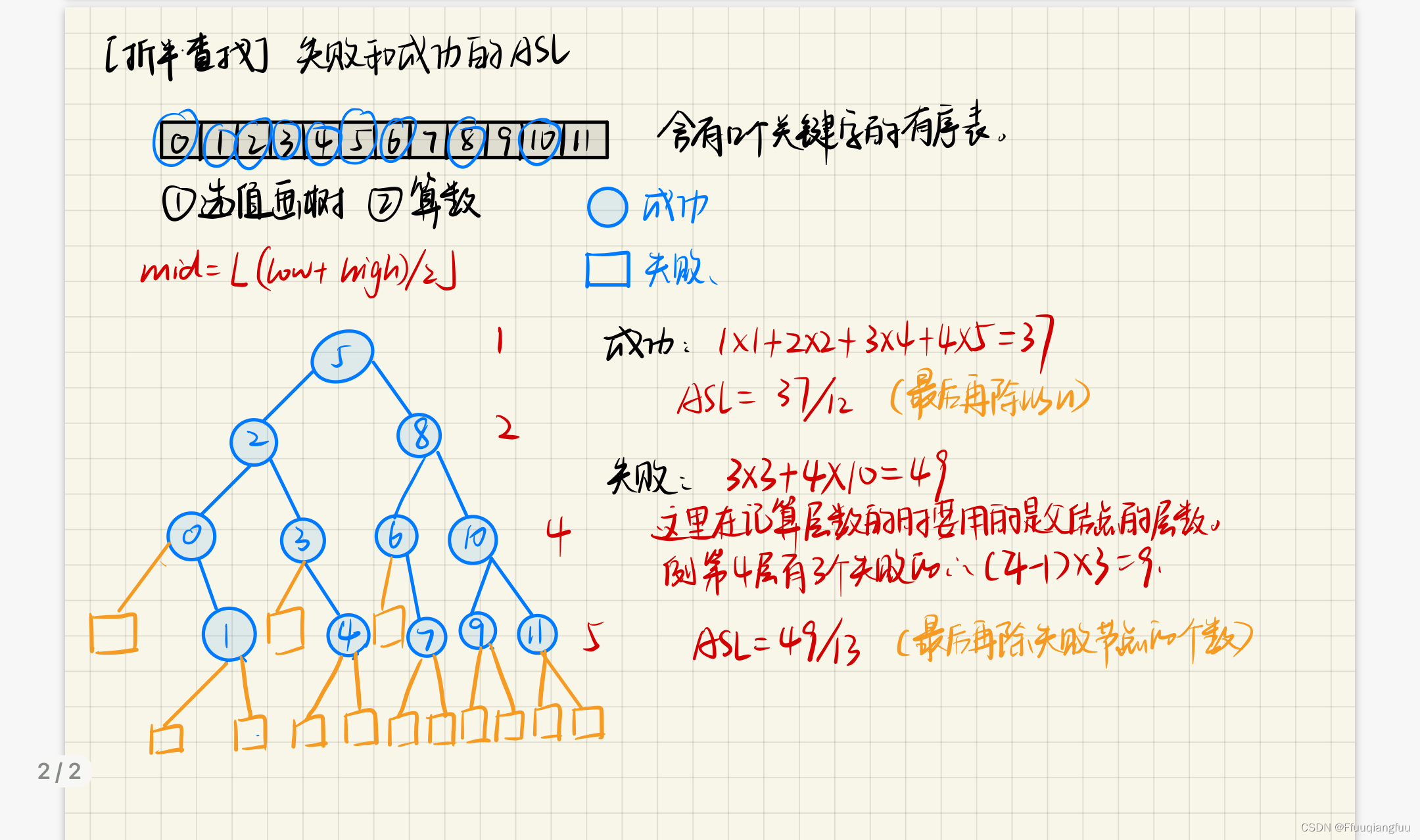
折半查找的时间复杂度为O（log2n）

分块查找

     分块查找就是将一个大的表分成几个子表，然后用索引表记录，索引表记录的是每个子表的最大的key跟该子表的开始位置是什么。查询的时候先确定自己的关键字在哪个子表，然后再在该子表中进行顺序查找，直到找到该值位置。

分块查找的ASL如下图所示

s是每块含有的记录数，n是一共有几块，b=n/s向上取整，当s取 n 时，ASLbs取最小值 根号n+1

优点：插入和删除元素的时候，只要找到该元素对应的块，就可以在该块内进行插入和删除运算。块内是无序的，所以插入删除比较容易

缺点：要增加一个索引表的存储空间

树表

二叉排序树

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树。

（1）若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；

（2）若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；

（3）它的左、右子树也分别为二叉排序树。

二叉排序树的递归查找

BiTree SearchBST(BSTree T, keyType key)

{

    if((!T)||key==T->data.key) return T;          //查找结束

    else if(key<T->data.key) return SearchBST(T->lchild,key);   //如果key的值小于当前节点的值就在左子树中递归查找

    else return SearchBST(T->rchild,key);         //在右子树中查找

}

为了使得二叉排序树的平均查找次数尽量的少，我们要使得二叉排序树尽量的平衡，这样就可以解决该问题。

二叉排序树的插入

void InsertBST(BSTree &T,ElemType e)

{//当二叉排序树T中不存在关键字等于e.key的数据元素时，则插入该元素

    if(!T)

    {               //找到插入位置，递归结束

        S=new BSTNode;//生成新节点*S

        S->data=e;//新节点*S的数据域置为e

        S->lchild=S->rchild=NULL;    //新节点*S作为叶子节点

        T=S;             //把新节点*S链接到已找到的插入位置

    }

    else if(e.key<T->data.key)

        InsertBST(T->lchild,e); //将*S插入左子树

    else if(e.key>T->data.key)

        InsertBST(T->rchild,e); //将*S插入右子树

}

二叉排序树插入的基本过程是查找，所以时间复杂度同查找一 样，是O(log2n)。

二叉排序树的创建

void CreatBST(BSTree &T)

{//依次读入关键字为key的节点，将相应节点插入二叉排序树T中

 T=NULL; //将二叉排序树T初始化为空树

 cin>>e;

 while(e.key!=ENDFLAG) //ENDFLAG为自定义常量，作为输入结束标志

 {

InsertBST(T,e);//将此节点插入二叉排序树T中

cin>>e;

 }

}

二叉排序树的删除要怎么进行

1）若p为叶子节点则可以直接删除

2）若p只有左子树或者右子树，直接让他们成为双亲结点就可以了

3）按中序遍历找到他的前驱或者后继来跟他进行替换，然后再进行删除就可以了。

平衡二叉树

如果数据有序排列，则二叉排序树是线性的，查找的时间复杂度为O(n)；反之，如果二叉 排序树的结构合理，则查找速度较快，查找的时间复杂度为O(log2n)。事实上，树的高度越小， 查找速度越快。

平衡二叉树或者是空树，或者是具有如下特征的二叉排序树：

（1）左子树和右子树的深度之差的绝对值不超过1；

（2）左子树和右子树也是平衡二叉树。

平衡二叉树的平衡调整方法

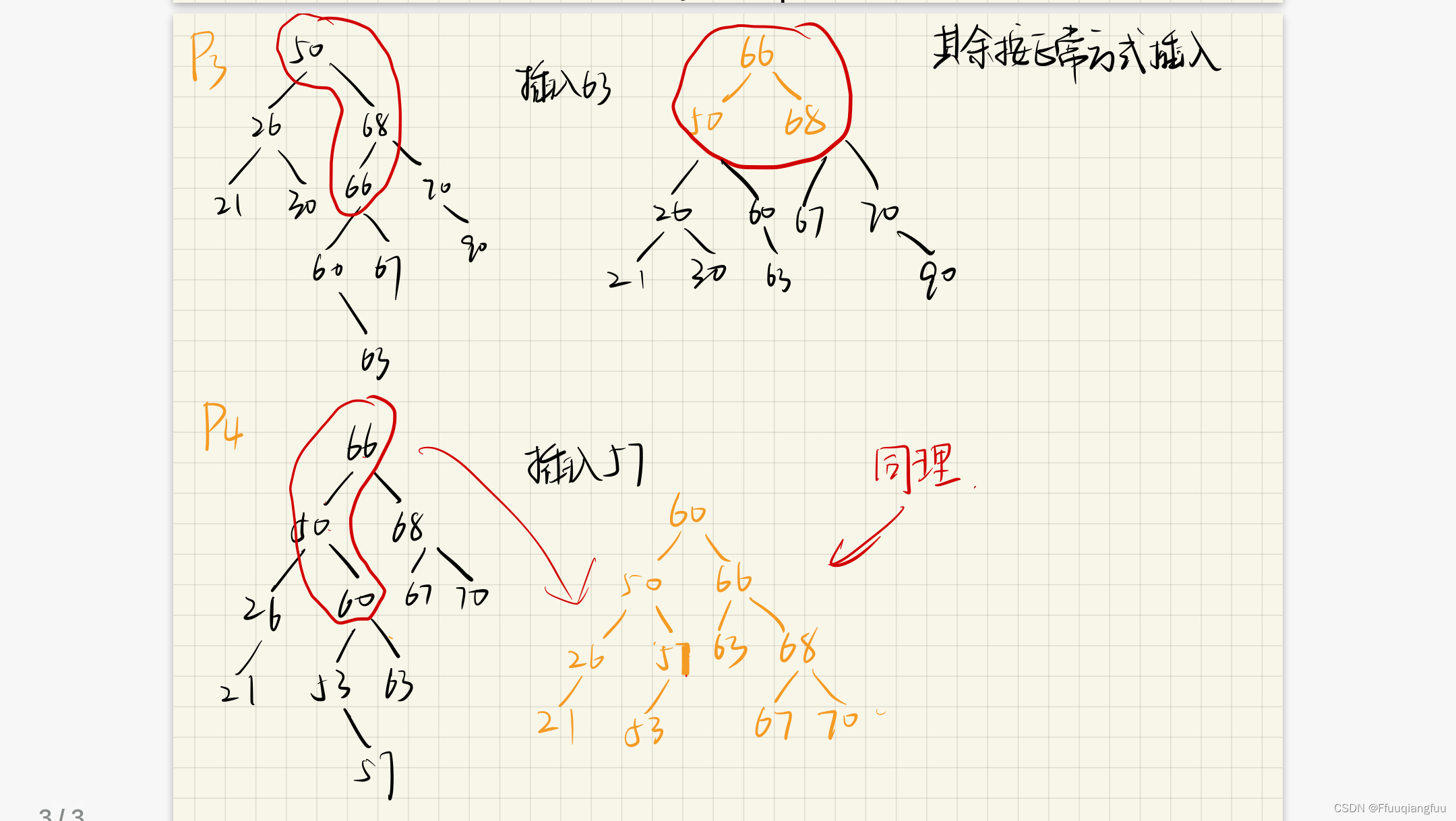
B-树

简单带过这个可能期末考的概率不大强烈推荐b站视频

【B-树的插入（创建）】 B-树的插入（创建）_哔哩哔哩_bilibili

【B树的插入删除】 B树的插入删除_哔哩哔哩_bilibili

删除根节点用左树的最大值或者右数的最小值来进行替换即可

散列表的查找

        如果能在元素的存储位置和其关键字之间建立 某种直接关系，那么在进行查找时，就无须作比较或只需作很少的比较，按照这种关系直接由 关键字找到相应的记录。这就是散列查找法（Hash Search）的思想，它通过对元素的关键字值 进行某种运算，直接求出元素的地址，即使用关键字到地址的直接转换方法，而不需要反复比较。

散列函数和散列地址：在记录的存储位置p和其关键字key之间建立一个确定的对应关系H，使p = H(key)，称这个对应关系H为散列函数，p为散列地址。

        散列表：一个有限连续的地址空间，用以存储按散列函数计算得到相应散列地址的数 据记录。通常散列表的存储空间是一个一维数组，散列地址是数组的下标。

散列函数的构造方法

1．数字分析法

假设某公司的员工登记表以员工的手机号作为关键字。手机号一共11位。前3位是接入号，对应不同运营商的子品牌；中间4位表示归属地；最后4位是用户号。不同手机号前7位相同的可能性很大。

所以可以采用后四位或者后四位逆转过来作为关键字

数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布比较均匀，就可以考虑这个方法。

2.直接定址法

取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a·key + b，其中a和b为常数（这种散列函数叫做自身函数）。

3.平方取中法

就是一个数平方后取中间的几位数，比如1234 平方为1522756 取中间三位227作为关键字.平方取中法比较适合于不知道关键字的分布，而位数又不是很大的情况。

4.折叠法

例如，当散列表长为1000时，关键字 key = 45387765213，从左到右每3位分为一 组，可以得到4个部分：453、877、652、13。 分别采用移位叠加和边界叠加，求得散列地址 为995和914

折叠法的适用情况：适合于散列地址的位 数较少，而关键字的位数较多，且难于直接从关键字中找到取值较分散的几位

5.除留余数法

假设散列表表长为m，选择一个不大于m的数p，用p去除关键字，除后所得余数为散列地址，即：

H(key) = key%p

可以选p为小于表长的最大质数

处理冲突的方法

 

1.开放地址法

通常把寻找“下一个”空位的过程称为探测，上述方法可用如下公式 表示

Hi = (H(key) +di)%m　i = 1, 2, …, k (k≤m − 1)

其中，H(key)为散列函数，m为散列表表长，di为增量序列。根据di取值的不同，可以分为以下3 种探测方法。

线性探测法

简而言之，如果冲突，就找下一个空的位置，直到找到为止

二次探测法

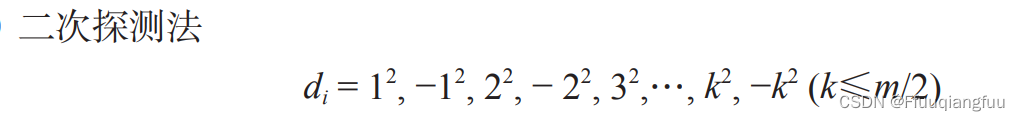
伪随机探测法：di = 伪随机数序列

2.链地址法

链地址法的基本思想是：把具有相同散列地址的记录放在同一个单链表中，称之为同义词 链表。有m个散列地址就有m个单链表，同时用数组HT[0…m−1]存放各个链表的头指针，凡是散 列地址为i的记录都以节点方式插入以HT[i]为头节点的单链表

装填因子 

散列函数的ASL的计算

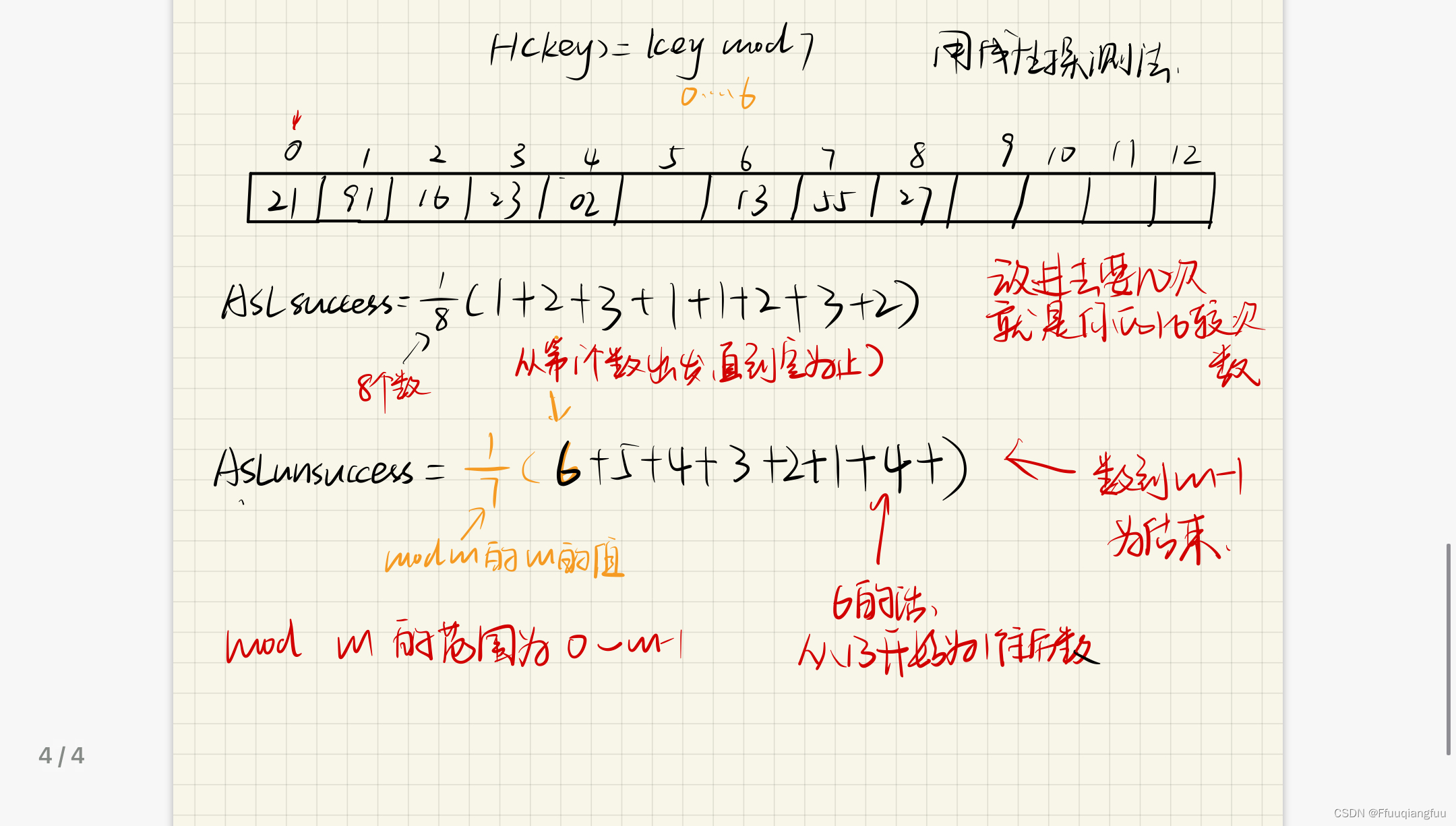
总结一下就是计算查找成功的ASL就是前面乘数字的个数，这里八个数字，就是八分之一，然后再乘每个数放入散列表需要的比较次数，如果一次哈希就可以放进去就是一，对于查找失败的则就是钱前面先乘1/m(m就是你散列函数mod后面的数字)然后从0开始到m-1，依次数第i个数到第一个空格也就是查找失败需要几次，比如上图，第一个数21到查找失败需要数6次才能到第五格那个空的位置，自己也要算进去。直到m-1也就是标志为6的那个格子