Codeforces Round #843 (Div. 2) C Interesting Sequence

最新推荐文章于 2025-12-02 15:32:05 发布

原创最新推荐文章于 2025-12-02 15:32:05 发布 · 219 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#算法

bitmask 专栏收录该内容

39 篇文章

订阅专栏

文章讨论了一种针对大整数n和x的算法问题，通过位操作和二分查找在O(logn)的时间复杂度内找到最小的m值。当n和x的特定位不匹配时，算法会更新边界并最终确定m。如果无法找到解决方案，则输出-1。

Problem - C - Codeforces

题意：

给定n和x，求最小的m使得：

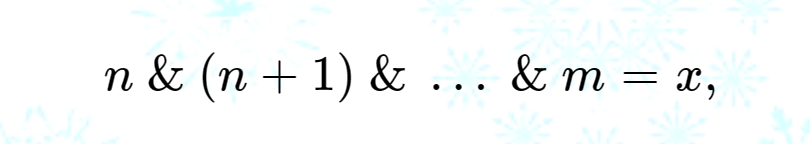
n和x范围是1e18

思路：

看到1e18，要不就是打表找规律，要不就是O(1)，要不就是O(logn)

因为这题是bitmask，因此按位考虑，是O(logn)的

让我们凭空求m，要不枚举，要不二分，要不直接求

枚举肯定不行

二分的话不能维护区间与的结果

因此我们根据n和x的位表示直接求m

Code：

#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,x;
void solve(){
    cin>>n>>x;
    bitset<64> b1(n),b2(x);
    int l=n,r=5e18;
    for(int i=63;i>=0;i--){
        if(b1[i]==0&&b2[i]==0) continue;
        else if(b1[i]==0&&b2[i]==1){
            cout<<-1<<'\n';
            return;
        }else if(b1[i]==1&&b2[i]==1){
            r=min(r,(n/(1ll<<i)+1)*(1ll<<i)-1);
        }else{
            l=max(l,(n/(1ll<<i)+1)*(1ll<<i));
        }
    }
    if(l<=r) cout<<l<<'\n';
    else cout<<-1<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;cin>>__;
    while(__--)solve();return 0;
}