Codeforces Round #815 (Div. 2) A-D2

CurleyD

已于 2022-08-25 08:41:45 修改

阅读量972

点赞数 7

CC 4.0 BY-SA版权

分类专栏： Codeforces 文章标签：算法

于 2022-08-19 01:59:10 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_62486861/article/details/126416582

Codeforces 专栏收录该内容

10 篇文章

订阅专栏

本文探讨了四个编程题目，涉及分数相等操作、序列最大和计算、矩阵操作计数及异或子序列问题。通过巧妙思路和优化算法，展示了从题意理解、策略设计到代码实现的过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

A. Burenka Plays with Fractions

D1. Xor-Subsequence (easy version)

题意:

思路:

code:

D2. Xor-Subsequence (hard version)

题意:

思路:

code:

题意:

给你两个分数, 每次选其中一个的分子/分母乘上任意一个数, 问你最少几次二者能够相等.

思路:

通分判断分子即可

相同:输出0.

不同但分子间能是倍数关系, 一次即可:输出1.

不同且不是倍数关系, 需要各乘一个数达到二者的LCM才行:即需要两次输出2.

坑点:通分显然会爆int

PS:我的写法因为0不能做分母, 故需要特判.

code:

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

void solve() {
    ll a, b, c, d;
    cin >> a >> b >> c >> d;
    
    //通分
    a = a * d, c = c * b;
    b = d = b * d;
    
    if (a == c)
        cout << "0\n";
    else if (a == 0 || c == 0)
        cout << "1\n";
    else if (a % c == 0 || c % a == 0 || a == 1 || c == 1)
        cout << "1\n";
    else   
        cout << "2\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;

    while (t--) {
        solve();
    }    

    return 0;
}

B. Interesting Sum

题意:

给你一个序列 $a_1...a_n$ , 让你选定一对 $(l,r)$ , 使得: $ans=max(a_1,a_2,...,a_{l-1},a_{r+1},a_{r+2},...a_n)-min(a_1,a_2,...,a_{l-1},a_{r+1},a_{r+2},...,a_n)+max(a_l,...,a_r)-min(a_l,...,a_r).$

取得最大值.

思路:

选定的l,r有四种情况可能贡献最大答案 a[l]最大a[r]最小最大次小次大最小次大次小

而这四种对答案的贡献其实都是a[maxn] + a[maxn-1] + a[minn] + a[minn+1].

因此排序后直接输出即可.

code:

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

void solve() {
    int n;
    cin >> n;

    vector<ll> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    sort(a.begin(), a.end());
    cout << a[n-1] + a[n-2] - a[0] - a[1] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;

    while (t--) {
        solve();
    }    

    return 0;
}

C. Corners

题意:

给你个01矩阵, 每次选择一个一定含有至少一个1的L型的子段, 让其中的元素全部变成0, 问你最多可以操作多少次.

思路:

观察样例1, 2的区别发现. 只要构造出了一个L型的全为0的子段, 那么之后从这个子段出发每次都可以构造出一个仅包含一个1的新L子段, 使得答案最大!

那么答案就是: 矩阵中1的个数 - 构建全为0的L子段所消耗掉的1的个数(除了L本身必须要有的那个以外的另外的1的数量). PS:消耗指的是浪费掉没用上的.

消耗的1有三种情况:1)矩阵全部为1一定消耗掉2个, 2)L中的两个为1会消耗掉1个, 3)L中只有一个为1不消耗.

接下来我们找最少消耗即可. 因为L有四种形状如图: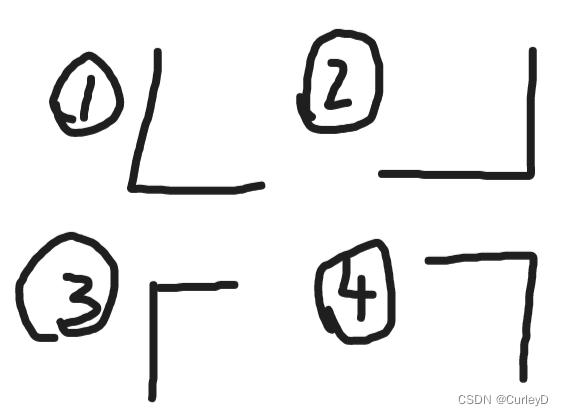

观察发现都会包含在一个2x2的正方形中, 因此可以按照2x2的正方形遍历矩阵来找会很方便.

code:

#include <bits/stdc++.h>

using namespace std;

int a[505][505];
char t[505][505];

void solve() {
    int n, m;
    cin >> n >> m;
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> t[i][j]; a[i][j] = t[i][j] - '0';
            cnt += (a[i][j] == 1);
        }
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (i + 1 <= n && j + 1 <= m && a[i][j] + a[i+1][j+1] + a[i+1][j] + a[i][j+1] <= 2) {
                cout << cnt << "\n";
                return;
            }
        }
    }

    if (cnt == n * m)
        cout << cnt - 2 << "\n";
    else   
        cout << cnt - 1 << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;

    while (t--) {
        solve();
    }    

    return 0;
}

D1. Xor-Subsequence (easy version)

题意:

给你一个序列, 让你求出最长的满足 $a_i \bigoplus j<a_j\bigoplus i,(i<j)$ 子序列 $a_1,a_2...a_n$

据说题意出锅了, 但我显然没发现, 毕竟我赛时想到做法没A出来555.

思路:

我们发现D1的数据范围中每个 $a_i$ 很友好只有不到200, 异或操作如果下标i和 $a_i$ 相差超过了 $a_i$ 的二进制下的上限256的话. 接下来所有的异或都只会得到256的值.

~~因此我们利用这个特征, 对于每个 $a_i$ 我们最多只向前找256个就可以, 再之前的话会有不会对答案产生贡献!~~

updata1: 2022/8/19

很抱歉之前的解释是错误且混乱的, 浪费了读者的时间, 万分抱歉. 已经参照CF的标准答案解释等进行更正.

(将之前的 j >= max(0, i - 256), 更改为了与推导过程同步的 j >= max(0, i - 255).

updata2: 2022/8/20

修正了dp转移方程只能逆向跑的错误, 个人习惯逆向写导致口胡, orz.

1.对题目进行理解:

我们每次要进行比较的是 $a_i\oplus j$ 和 $a_j\oplus i$ . 但为了贴合下文操作我们将上述两个异或改写成 $j\oplus a_i, i \oplus a_j$ , 其中i , j会增大( j < i), 而ai, aj 则始终 <= 200 (即二进制下不超8位).

2.设置:

我们用dp[i]表示从第1个开始到第i个满足题目条件的最长子序列的长度. 并且我们将i, j分别称为当前状态和之前状态.

3.转移方程:

先看一个暴力的做法: 从1枚举到n, 每次先设置dp[i] = 1,因为自己一定形成一个(算是初始化?)

再令 j 从i - 1向前枚举检查是否满足 $a_j\oplus i<a_i\oplus j$ , 若满足更新dp[i]为max(dp[i], dp[j] + 1).

~~(注意不是令j从0到i-1枚举, 这个原因和背包问题的优化的从后向前枚举是一个道理, 不做说明了)~~

从前向后枚举一样可以, 都会被算到, 本质上完全一致!, 只不过写法不同! (01背包优化避免重复取的才只能逆向跑)

本文下面的代码也可以正向写成

 for (int j = max(0, i - 255); j <= i - 1; j++)

4.优化 / 减少开销:

我们可以发现上面的两个异或操作 $j\oplus a_i, i \oplus a_j$ 实际上相当于每次只对i 或 j的二进制下的前8位进行更改, 而对前8位以外的部分不会产生影响! 原因是 $a_i,a_j$ 不超过200, 二进制下也就是不超过前8位, 异或上去后只能影响前8位, 因此我们可以借此进行优化!

下面看一个例子来解释上面这句话:ai = 200, j = 1234和 j = 2021

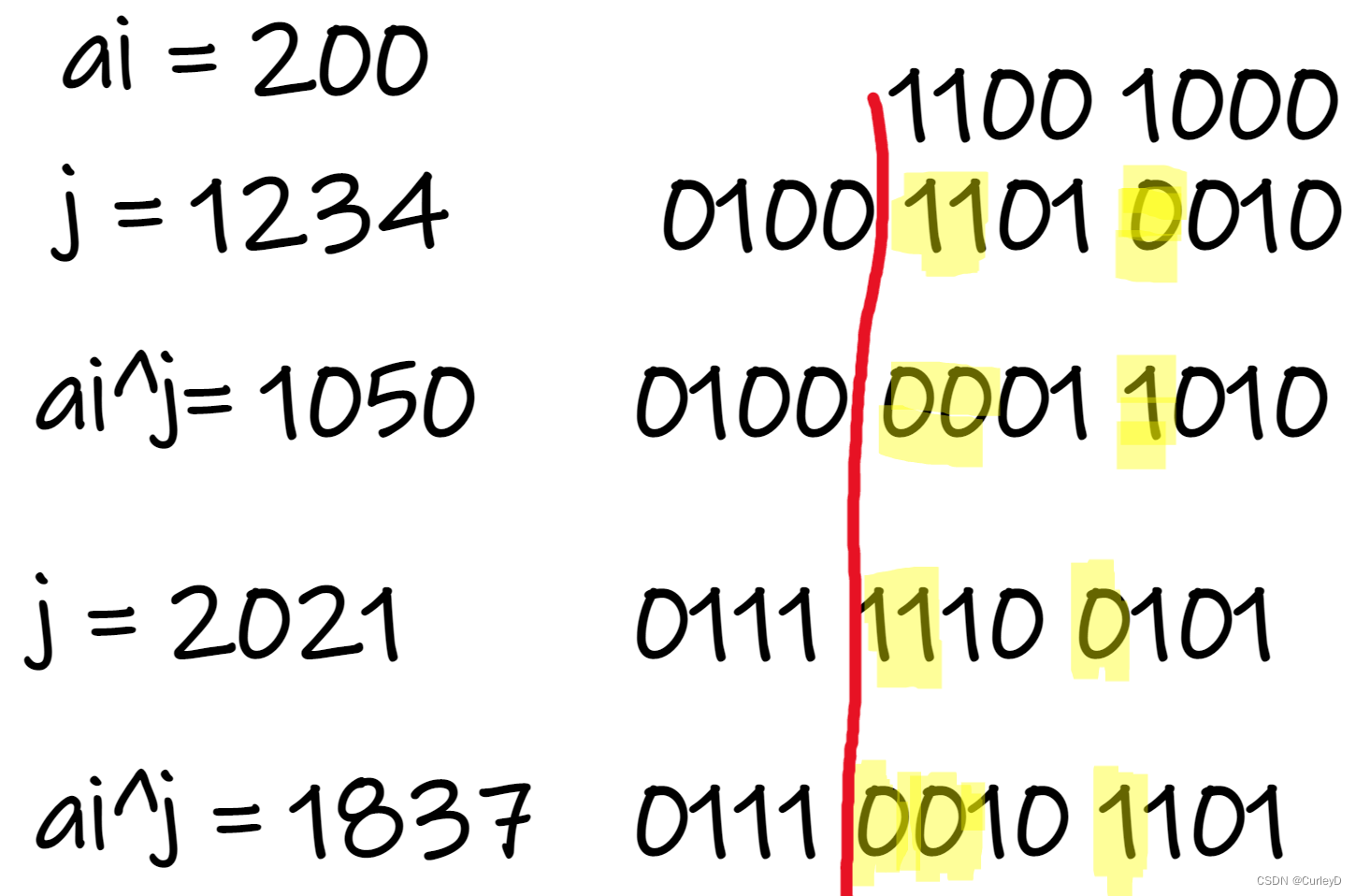
那既然每次只会对前八位产生影响. 那是不是证明了能够转移到当前状态i的之前状态j与i的差值一定是在这前8位的 $2^0+2^1+...+2^7=255$ 之间! 因此我们不需要从i-1枚举到0, 我们只需要枚举那些能够转移的之前状态 j 即(i - 1 ~ i - 255), 再进行 $a_i\oplus j$ 和 $a_j\oplus i$ 的大小比较更新dp[i]即可.

5.收尾:

因此这个限制大大减少了不必要的逆向查找, 这也是我们可以用线性dp来做的真正原因, 问题就转化成了一个简单的线性dp问题, 我们扫一遍即可得到答案. 最后输出dp中最大的即可!

code:

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

void solve() {
    int n;
    cin >> n;
    
    vector<ll> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }

    vector<ll> dp(n);
    for (int i = 0; i < n; i++) {
        dp[i] = 1;
        for (int j = i - 1; j >= max(0, i - 255); j--) { 
            if ((a[i] ^ j) > (a[j] ^ i)) { //注意加括号!
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
    }
    
    cout << *max_element(dp.begin(), dp.end()) << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int t;
    cin >> t;
    
    while (t--) {
        solve();
    }
    
    return 0;
}

D2. Xor-Subsequence (hard version)

题意:

同上

思路:

jls用trie树 + dp做的, jls真是tql, 直接贴jls的代码了.

太优雅了写的orz.

code:

#include <bits/stdc++.h>

using i64 = long long;

constexpr int N = 300000 * 31;

int cnt;
int trie[N][2];
int f[N][2];

int newNode() {
    ++cnt;
    trie[cnt][0] = trie[cnt][1] = 0;
    f[cnt][0] = f[cnt][1] = 0;
    return cnt;
}

void solve() {
    int n;
    std::cin >> n;
    
    std::vector<int> a(n);
    for (int i = 0; i < n; i++) {
        std::cin >> a[i];
    }
    cnt = 0;
    newNode();
    
    std::vector<int> dp(n);
    for (int i = 0; i < n; i++) {
        int x = a[i] ^ i;
        int p = 1;
        for (int j = 29; j >= 0; j--) {
            int v = x >> j & 1;
            dp[i] = std::max(dp[i], f[trie[p][!v]][i >> j & 1]);
            p = trie[p][v];
            if (!p) {
                break;
            }
        }
        dp[i]++;
        p = 1;
        for (int j = 29; j >= 0; j--) {
            int v = x >> j & 1;
            if (!trie[p][v]) {
                trie[p][v] = newNode();
            }
            p = trie[p][v];
            int &res = f[p][a[i] >> j & 1];
            res = std::max(res, dp[i]);
        }
    }
    
    
    int ans = *std::max_element(dp.begin(), dp.end());
    std::cout << ans << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int t;
    std::cin >> t;
    
    while (t--) {
        solve();
    }
    
    return 0;
}

小结

最近睡眠不规律, 21:35开始, 我21:10才起来. 开始半个小时脑子还在睡眠状态, 之后精神了些赶紧写掉了A题, B题想复杂了, 当时应该看眼榜的, 好多人3min就A掉的也就是这种类似结论题的了. 推了下结论过了, C没什么障碍, 就是写代码第一次写的又臭又长, 后来发现直接检查2x2正方形就行...

D1开始以为转化成最长上升子序列的O(NlogN)那个做法, 后来发现不太可行, 要结束了发现数据范围的意义但来不及了...

总体来看这场基本都是思维题, 码量小, 多动脑, 想通了一道题后基本直接出了没太大实现难度, 偶尔做做思维体操也挺有意思的. 也挺幸运这么慢出A和B居然还能rank不低. 第一次摆脱了灰名newbie, 成为了绿名pupil, 感觉还是要更加努力些, 多补题, 多学新东西.