代码随想录训练营第五十五天| 392.判断子序列、115.不同的子序列

392.判断子序列

题目链接/文章讲解/视频讲解：代码随想录

1.代码展示

//392.判断子序列
bool isSubsequence(string s, string t) {
	//step1 构建dp数组
	//dp[i][j]的含义是以下标i - 1为结尾的字符串s，以下标为j - 1为结尾的字符串t，
	//相同子序列的长度为dp[i][j]
	vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
	//step2 状态转移方程
	//情况1：当s[i - 1] == t[j - 1]时，此时相等，则dp[i][j] = dp[i - 1][j - 1] + 1;
	//情况2：当不等于时，此时相当于把t[j - 1]删掉，则dp[i][j] = dp[i][j - 1];;
	//step3 初始化都为0
	//step4 开始遍历
	for (int i = 1; i <= s.size(); i++) {
		for (int j = 1; j <= t.size(); j++) {
			if (s[i - 1] == t[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else {
				dp[i][j] = dp[i][j - 1];
			}
		}
	}
	if (dp[s.size()][t.size()] == s.size()) {
		return true;
	}
	return false;
}

2.本题小节

        思考：dp[i][j]的含义是以下标i - 1为结尾的字符串s和以下标为j - 1为结尾的字符串t的相同子序列的长度为，本题的重点在于对状态转移方程的理解，一共有两种情况，当s[i - 1] == t[j - 1]时，则，dp[i][j]由dp[i - 1][j - 1]推出来，如果不相等，则相当于把t中的t[i - 1]删掉，再寻找，即dp[i][j] = dp[i][j - 1]（以i - 1结尾的s 和 以 j - 2结尾的t），最后结果返回dp右下角即可。 

        基本思路：见代码，主要要根据题意理解状态转移方程

115.不同的子序列  

 题目链接/文章讲解/视频讲解：代码随想录

1.代码展现

//115.不同的子序列
int numDistinct(string s, string t) {
	//step1 构建dp数组
	vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));
	//step2 状态转移方程
	//情况1：当s[i - 1] == t[j - 1]时，此时相等，则dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
	//情况2：当不等于时，此时相当于把t[j - 1]删掉，则dp[i][j] = dp[i - 1][j];
	//step3 初始化
	for (int i = 0; i <= s.size(); i++) {
		dp[i][0] = 1;
	}
	//step4 开始遍历
	for (int i = 1; i <= s.size(); i++) {
		for (int j = 1; j <= t.size(); j++) {
			if (s[i - 1] == t[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
			}
			else {
				dp[i][j] = dp[i - 1][j];
			}
		}
	}
	return dp[s.size()][t.size()];
}

2.本题小节

        思考：dp[i][j]的含义是以下标i - 1为结尾的字符串s和以下标为j - 1为结尾的字符串t，s中含有t的子序列的个数，本题的重点也是要理解状态转移方程， 一共有两种情况，当s[i - 1] == t[j - 1]时，则此时dp[i][j]可以由两种情况推出来，一种是dp[i - 1][j - 1]（下标为i - 2的s和下标为j - 2的t），另外一种dp[i - 1][j]（下表为 i - 2的s和下标为j - 1的t），即dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]，当不相等时，dp[i][j] = dp[i - 1][j]，此时相当于删掉了s中的最后一位

        基本思路：弄懂状态转移方程，具体步骤见代码。

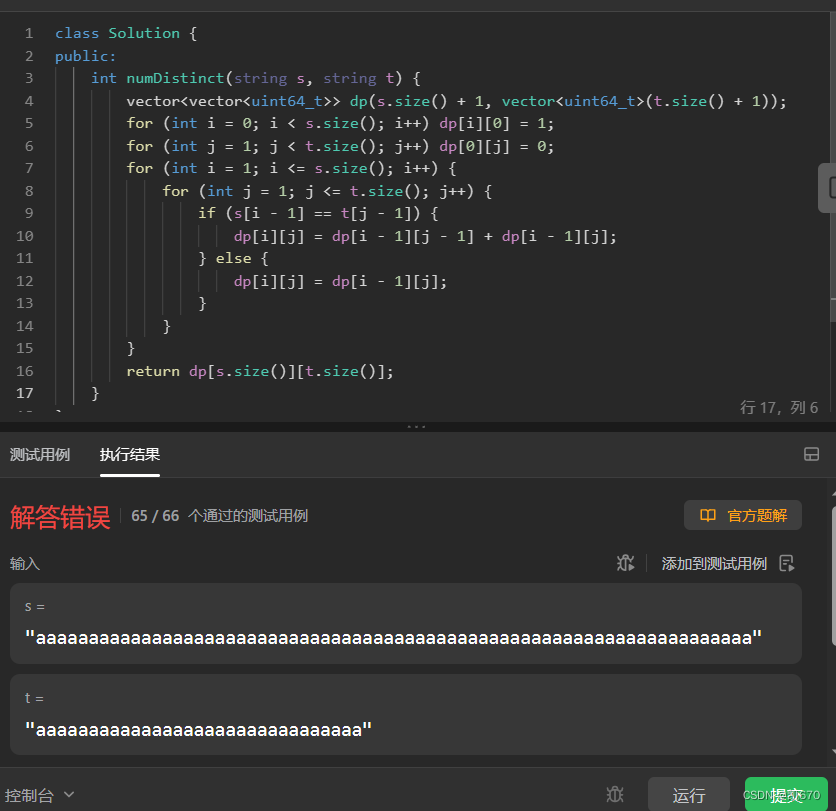
小插曲，卡哥给得代码出错，不知道啥情况，这题理解起来有点费劲