本文介绍了桥式构建法构建单偶幻方，这种方法比斯特雷奇法更简单易记。通过填充色块、特定顺序填数及巧妙换位，可以便捷地构建高阶幻方。详细步骤包括填充灰色和白色块，然后进行纵轴和横轴的数字换位，最终调整特定位置的数字，实现幻方构建。文中还提供了10阶、14阶和6阶幻方的实例及斯特雷奇法的影印介绍。
单偶幻方的构建，最常用的方法，似属斯特雷奇法。该方法，要把所给数列均分为四组，每组用奇阶的罗伯法构造，且一定要按要求排序，还要特别繁琐的不易记住的复杂换位，才得结果。阶数越高，换位成列增加，不很方便（附录中有斯特雷奇法的影印介绍，选自《幻方与素数》一书）。
我发现的这种桥式构建法，连写而就，一说就会。且阶数的增加，只多几个数字换位。方法简单，容易记忆，比斯特雷奇法，应该方便得多。
本构造法的便捷，完全得益于至关重要的桥型阴影色块的构思，所以称之为桥式构建法。
下面用10阶幻方为例子加以说明。
1、填充色块，除了中间两块（所谓桥）连续外，其它色块都是间隔的。
2、填数
1）由第一格开始，从上到下，连报跳写：只填灰色块，不填白色块，一直写到最后，如图一（从白色块始填也行，但要一种色块填到底）。
2）然后，反向逆序，从下到上，从头开始，连报跳写：只填白色块，不填灰色块（灰色块已填），结果如图二。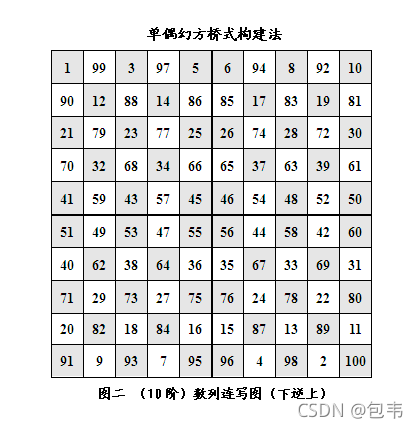
3、换位：</
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
