线性回归&逻辑回归

 线性回归

其中，x是特征，y是标签，w为权重。

举个例子，y是谈恋爱成功率，x1是长得帅，x2是有钱，x3是情商高。

那么每个人对于这三点的权重w1，w2，w3 都是不一样的，如果同学A长得很帅那么他的w1的值就很大，但是不咋有钱情商不咋高，那么w2，w3平平无奇；同学B长相普通，w1的值就很小，但很有钱，情商也很高，那么w2，w3的值很大，那么最后的B的f(x)的值也会很大，值越大越能说明他谈恋爱的成功率很高。这个b是什么呢？b是一个随机值，为了符合客观的整体规律而添加上去的。

好了，现在我们知道这个公式的含义了，接下来我们要学习一个函数：误差函数

为了判断真实值和我们模型预测值的差距，我们需要引入这个函数，loss的值越小，说明我们的模型越准确，其中f(x)=wx+b，y是真实值，m是样本数，那么想要计算出loss，最关键的在于w如何求解，这个权重是多少，才能够使得我们的loss值最小呢？

方法一：穷举法   

这个方法很简单，就是让计算机自己随便取值，没有规律，然后计算loss，看看w取哪个值的时候loss最小，那么我们就找到所需的w值了。这个方法很简单，但是想找到我们想要的w太随缘了，效率太低。

方法二：最小二乘法

我们观察这个loss函数，其实不就是一个二次函数吗，影响loss值的参数就是w，那找最值就是让loss函数对w求导呗，如下图所示

 

当然，这是最简单的一个loss函数了，实际上loss函数中的w不止一个，由于问题的复杂性的提高，影响最终结果的w也会有很多，那我们可以先把 f(x) 抽象成一个矩阵。如图所示，再写出我们的loss函数。 

 

好了，接下来我们就对w求偏导再令其为0，就可以得出我们所想要结果了

很好，现在我们已经求出想要的w了，那么什么时候都能用最小二乘法来找到w吗？

当然不是，w = 逆矩阵 X 两个普通的矩阵， 但是这个逆矩阵一定存在吗？那当然不一定了

所以我们引出我们的另一个方法来找w。

方法三：梯度下降法（核心！）

梯度是什么？简单来说，梯度就是loss函数对w的导数，在此后的深度学习中，我们会经常遇到这个概念，我们的目的很简单，就是找到loss最小时，w的值，这张图很直观给我们解释。

 

最低点就是我们所想要的点，这个公式中，a就是每次移动时的步长（即学习率），步长过大可能找不到最低点，步长过小会导致模型调节的速度过慢，一般来说a需要自己设定一个合适的值。当梯度不为0的时候，w的值会一直更新，当梯度为0时，w找到了最小的点。这是一个参数w的情况，如果有w1，w2...wn呢？那就对它们求偏导。

为了更好的理解梯度更新，我们举一个例子。

我们光看就这个公式可以知道w最合适的值是0，此时loss函数最小为0，但我们可以通过公式计算来演练梯度下降的过程，还有一点，就是关于a即学习率对w更新的影响，当学习率从0.1变成0.5时，我们就很难找到w为0的点了，所以学习率的设置一定要合理。一般取0.01，0.001。

基础知识我们已经学会了，现在开始实战。

# 定义数据集

# 定义数据特征
x_data = [1, 2, 3]

# 定义数据标签
y_data = [2, 4, 6]

# 初始化参数W
w = 4

# 定义线性回归的模型
def forword(x):
    return x * w

# 定义损失函数
def cost(xs, ys):
    costvalue = 0
    for x, y in zip(xs, ys):
        y_pred = forword(x)
        costvalue += (y_pred-y)**2
    return costvalue / len(xs)

# 定义计算梯度的函数
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w -y)
    return grad / len(xs)


for epoch in range(100):
    cost_val = cost(x_data, y_data)

    grad_val = gradient(x_data, y_data)

    w = w - 0.01 * grad_val


    print('训练轮次：', epoch, "w=", w, "loss", cost_val)


print("100轮后w已经训练好了，此时我们用训练好的w进行推理，学习时间为4个小时的时候最终的得分为：", forword(4))

逻辑回归

线性回归的输出是连续的，直接预测数值，就比如刚刚的实战例题，预测学习4小时获得8分，学习5小时就获得10分；而逻辑回归是根据线性回归的值进行分类的，它的输出会经过sigmoid函数转换成概率值，这个概率在0到1之间，然后根据阈值进行分类。那首先我们要了解什么事sigmoid函数。

sigmoid函数

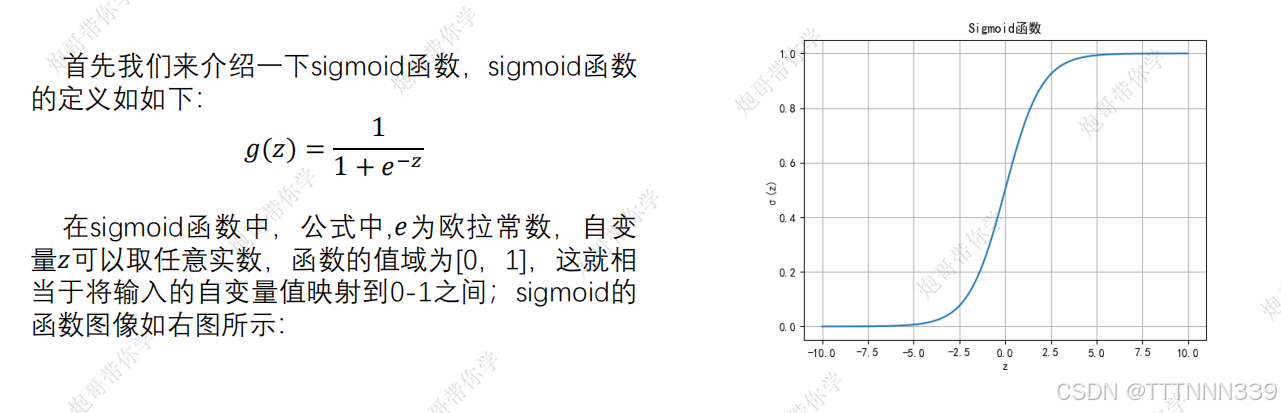
当z趋向于负无穷的时候，g(z)的值是趋于0的，当z趋于正无穷的时候，g(z)的值是趋于1的

那么它是怎么跟线性回归联系起来的呢？那就是z

为了更好的理解逻辑回归的目的，就举上面的例子，判断一个人有没有谈过恋爱（结果只有两种谈过/没谈过，注意区分上面的例子，谈恋爱的成功率，成功率可能是50% 80% 90%，它是多种连续的数值结果）。同学A，长得帅，有钱，情商高，那么把这些数据带入公式求出z，那我们求出的z的值肯定是很大的，那我们可以设定，g(x) 的值超过0.6就判断这个人谈过，如果g(x) 的值小于0.6就判断他没谈过。

好了，现在我们理解了逻辑回归大概是干什么的——分类

那么问题来了，想要知道概率值，我们最重要就是求z的值，那么想要求z，那不就是求权重w和偏置项b嘛，那我们之前在线性回归中求w的时候，是通过一个简单loss函数来找到我们想要的w和b的，那么现在该如何找到w和b呢？

依旧是通过我们loss函数，但是这边的loss函数更加复杂一些，我认为不太需要详解，流程一样。

使用AI对比一下这两个回归模型。

现在开始逻辑回归的实战——利用逻辑回归进行乳腺癌的分类检测

数据文件我放在这篇文章的附件中了，可以自己去实现一下

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import minmax_scale, MinMaxScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report

#读取数据

dataset=pd.read_csv("breast_cancer_data.csv")
# print(dataset)

#提取x
X=dataset.iloc[:,:-1] #最后一列不要，其他列都要
# print(X)

#提取数据中的标签
Y=dataset['target']
# print(Y)

#划分数据集和测试集
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2)   #80%测试集 20%测试集

#进行数据的归一化
sc=MinMaxScaler(feature_range=(0,1))#归一化到0~1之间
x_train=sc.fit_transform(x_train)
x_test=sc.transform(x_test)
# print(x_train)

#逻辑回归模型搭建
lr=LogisticRegression()
lr.fit(x_train,y_train)

#打印模型的参数
# print(':w',lr.coef_)
# print(':b',lr.intercept_)

#利用训练好的模型进行推理测试
pre_result=lr.predict(x_test)

# print(pre_result)

#打印预测结果的概率
pre_result_proba=lr.predict_proba(x_test)
# print(pre_result_proba)

#获取恶性肿瘤的概率
pre_list=pre_result_proba[:,1]
# print(pre_list)

#设置阈值
thresholds=0.3

#设置保存结果的列表
result=[]
result_name=[]
for i in range(len(pre_list)):
    if pre_list[i]>thresholds:
        result.append(1)
        result_name.append('恶性')
    else:
        result.append(0)
        result_name.append('良性')

#打印阈值调整后的结果
# print(result)
# print(result_name)

#输出结果的精确率和召回率还有f1值
report=classification_report(y_test,result,labels=[0,1],target_names=['良性肿瘤','恶性肿瘤'])
print(report)