KMP算法，看完这篇你就懂了

目录

1.朴素算法

2.next数组

3.kmp算法

4.例题

---

所谓kmp算法，本质上就是字符串匹配问题，接下来我们从暴力算法进行一步步优化。

1.朴素算法

给出两个字符串，p为短串，s为长串。一般s串叫作文本串，p串叫作模式串，需要判断p串是不是s串的子串，例如：s="abababa"，那么p="aba"就是s串的子串，而p="ababc"就不是s串的子串。暴力的方法非常简单，只要让指针i从文本串的起始位置开始逐位与模式串进行比较，如果匹配过程中每一位都相同，则文本串与模式串匹配。否则，只要出现某一位不同，则文本串的起始位置就变为i+1，并从头开始模式串的匹配。但是这种算法的时间复杂度为O(nm),其中n,m分别为文本串，模式串的长度，显而易见，当n,m都达到10的5次方级别的时候完全无法承受。

下面代码为文末例题的暴力算法，结果正确，但是时间超限。所以我们将kmp的暴力算法进行优化

#include <iostream>
using namespace std;
const int N = 100010,M = 1000010;
int n,m;
char p[N],s[M];
int main()
{
    //s为长字符串，p为短字符串
    cin>>n>>p>>m>>s;
    for(int i=0;i<m;)
    {
        //记录此次数组开始位置
        int start=i,j=0;  
        while(i<m&&j<n&&s[i++]==p[j++]);//两个字符串一直比较，直到不相等
        if(j==n)//如果p串即短串比较完成
        {
            cout<<start<<" ";
            
        }
       
        i=start+1;//每轮循环结束后i更新
    }
    
   return 0; 
}

在讲解kmp算法之前我们先给大家介绍一下next数组(暂时不必纠结数组名称问题)

2.next数组

假设有一个字符串s(我们这里设置下标从0开始)，那么这个数字以i结尾的子串就是s[0,i],对于该子串来说，长度为k的前缀和后缀分别是s[0,k],s[i-k,i]。现在定义一个next数组，其中next[i]表示使子串s[0,i]的前缀s[0,k]等于后缀s[i-k,i]的最大的k(此处注意前缀和后缀可以重合，但不能是子串本身)，如果找不到相等的前后缀，那么next[i]返回-1，所以，next数组就是最长相等的前后缀中前缀的最后一位的下标。

以字符串s="ababaab"作为举例，next数组如图所示，读者可以结合图2.1.1理解。图示将子串s[0,i]写在两行，第一行提供后缀，第二行提供前缀，并将相等的前后缀用红框框起来。

 图2.1.1

 图1：i=0，子串s[0,i]为"a",由于找不到相等的前后缀(前后缀均不能是s[0,i]本身，下同），因此next[0]=-1。

图2：i=1,子串s[0,i]为"ab",由于找不到相等的前后缀，因此next[1]=-1。

图3：i=2，子串s[0.i]为"aba",能使前后缀相等的最大的k为1，当k=1时，后缀s[i-k,i]为"a",前缀s[0,i]为"a"；而当k=2时，后缀s[i-k,i]为“ba",前缀s[0,i]为"ab",它们不想等，因此next[2]=0。

图4：i=3，子串s[0,i]为"abab",能使前后缀相等的最大的k为2，当k=2时，后缀s[i-k,i]为"ab",前缀s[0,i]为"ab"；而当k=3时，后缀s[i-k,i]为“bab",前缀s[0,i]为"aba",它们不想等，因此next[3]=1。

图5：i=4，子串s[0,i]为"ababa",能使前后缀相等的最大的k为3，当k=3时，后缀s[i-k,i]为"aba",前缀s[0,i]为"aba"；而当k=4时，后缀s[i-k,i]为“baba",前缀s[0,i]为"abab",它们不想等，因此next[4]=2。

图6：i=5，子串s[0,i]为"ababaa",能使前后缀相等的最大的k为1，当k=1时，后缀s[i-k,i]为"a",前缀s[0,i]为"a"；而当k=1时，后缀s[i-k,i]为“aa",前缀s[0,i]为"ab",它们不想等，因此next[5]=0。

图6：i=6，子串s[0,i]为"ababaab",能使前后缀相等的最大的k为2，当k=2时，后缀s[i-k,i]为"ab",前缀s[0,i]为"ab"；而当k=3时，后缀s[i-k,i]为“aab",前缀s[0,i]为"aba",它们不想等，因此next[6]=1。

再强调一遍，next[i]就是子串s[0,i]的最长相等前后缀的前缀的最后一位的下标。读者可以手动尝试一下字符串"abababc"的next数组，可以得到[-1，-1，0，1，2，3，-1]

相信到了这里，读者已经知道了什么是next数组了。

接下来，我们讲解如何去求next数组，暴力方法可以求吗？可以 ，但是暴力方法求效率低下，我们这里采用”递推“的方法来高效求解next数组，即假设已经知道next[0],...next[i-1]的值，求解next[i]的值。

作为举例，假设已经知道了next[0]=-1,next[1]=-1,next[2]=0,next[3]=1，现在来求next[4]。

 图2.1.2 next[4]求解过程图

 如图2.1.2所示，当已经得到next[3]=1时，最长相等前后缀等于“ab",之后在计算next[4]时，由于s[4]==s[next[3]+1]，因此可以把最长相等的前后缀"ab"扩展为"aba"，因此next[4]=next[3]+1=3，并令j指向next[4]。

但是按照此想法求解next[5]时，发现s[5]!=s[next[4]+1],糟糕！那就不能通过扩展最长相等的前后缀的方法求解next[5]，即不能通过next[4]+1的方法得到next[5]。这个时候应该怎么办呢？既然相等的前后缀没有办法达到那么长，那么不妨缩短一点！此时希望找到一个j，使得s[5]==s[j+1]成立，

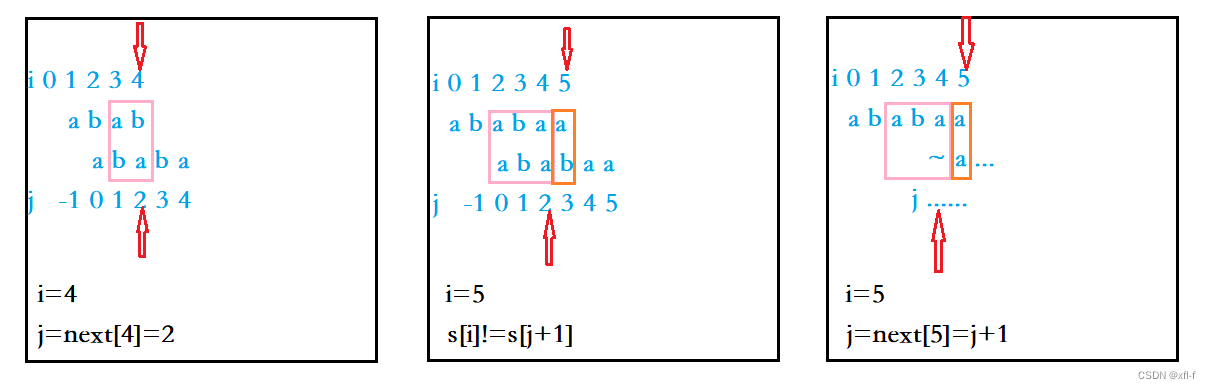
 图2.1.3 next[5]模仿next[4]求解失败示意图

同时图中的波浪线~（代表s[0,j]）是s[0,2]="aba"的后缀（而s[0,j]也是s[0,2]的前缀也是显而易见的）。同时要求相等的前后缀尽可能的长，也就是j尽可能的大。

实际上在要求图中的波浪线“~”部分（即s[0,j]）既是s[0,2]的前缀，也是s[0,2]的后缀，同时希望相等的前后缀的长度尽可能的长。即s[0,j]就是s[0,2]的最长相等前后缀。也就是说，只要让j=next[2]，然后再判断s[5]==s[j+1]是否成立。如果成立，那么就说明s[0,j+1]是s[0,5]的最长相等前后缀，再令next[5]=j+1即可；如果不成立，就不断令j=next[j]，直到j=-1或者找到s[5]=s[j+1]成立。

如图2.1.4所示，j从2回退到next[2]=0处，发现s[5]==s[j+1]不成立，就继续让j回退到next[0]=-1；此时，由于j已经回退到了-1，因此不再继续回退，这时发现s[i]==s[j+1]成立

 图2.1.4 next[5]求解过程

 说明s[0,j+1]是s[0,5]的最长相等前后缀，于是令next[5]=j+1=0,并令j指向next[5]。最终结果如图2.1.5所示。

 图2.1.5 next[5]求解结果

 由以上的例子可以发现，每次求出next[i]的时候，会让j指向next[i]，以方便求解next[i+1]。由此退出next[0]=-1一定成立（思考一下原因），因此初始情况下可以令j=-1。

下面总结一下next数组的求解过程：

（1）初始化next数组，并令j = next[0] = -1。

（2）让i在字符串长度大小范围内进行遍历，对于每个i，重复（3）（4）步骤，求解next数组

（3）当j!=-1且s[i]!=s[j+1]的时候，不断令j=next[j],直到j退回-1，或者找到s[i]==s[j+1]

（4）如果s[i]==s[j+1],则next[i]=j+1（即j++），否则的话就next[i]=j。

3.kmp算法

在上面的基础上，我们正式进入kmp算法的讲解。大家会发现，有了上面的基础，kmp算法是在照葫芦画瓢。此处给出一个文本串s和一个模式串p，然后判断模式串是否为文本串的子串。

以s="ababaabc",p="ababaab"为例子，令i指向s的当前欲比较位，令j指向p中当前已被匹配的最后一位，这样只要说明s[i]==p[j+1]，就说明p[j+1]也被匹配成功，这样i，j就可以+1继续进行匹配。

而当遇到s[i]!=p[j+1]的情况，是不是跟求next数组的情况十分类似呢？也就是说，只需要不断让j回退到next[j]，知道j=-1或者s[i]==s[j+1]成立，然后继续匹配即可。从这个角度来说，next数组的含义就是当j+1位失配时，j应该回退到的位置。

因此可以总结出kmp算法的一般思路：

（1）初始化j=-1,表示p当前已被匹配的最后位。

（2） 让i遍历文本串s，对每个i，执行步骤（3）（4）来试图匹配s[i]和p[j+1]。

（3）当j！=-2且s[i]!=p[j+1]时，不断令j=next[j]，直到j回退到j=-1或者s[i]==p[j+1]。

（4)如果s[i]==p[j+1]，则令j++。如果j达到m-1（即模式串最后一位匹配完成），说明p是s的子串。

4.例题

我们接下来看一道关于kmp的算法题。

给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式

第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P。

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S。

输出格式

共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围

1≤N≤10^5
1≤M≤10^6

输入样例：

3
aba
5
ababa

输出样例：

0 2

注意：

（1）我们此处的模板是将数组从1开始，上面所讲的内容数组是从0开始，读者们可以自己尝试一下数组从0开始的代码。

（2）题目要求：

模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

说明p串在s串可以多次出现，而我们上面讲解的只是判断p串是否为s串的子串。

如图4.1所示，当p串已经匹配完成后，i+1位就没有与之匹配的p了，所以说我们就要尽可能小的将j往前移位，同时使p串的前缀后缀相等且最大，这就又回到以前的问题了，所以每当j匹配完成后，就让j=next[j]。

图4.1  注意事项解答

根据上面讲解的知识，可以得出：

#include <iostream>
using namespace std;
const int N=100010,M=1000010;
int n,m;
char p[N],s[M];
int ne[N];
int main()
{
    cin>>n>>p+1>>m>>s+1;
    //求解next数组
    for(int i=2,j=0;i<=n;i++)
    {
        while(j&&p[i]!=p[j+1]) j=ne[j];
        if(p[i]==p[j+1]) j++;
        ne[i]=j;
    }
    //kmp算法匹配过程
    for(int i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1]) j=ne[j];
        if(s[i]==p[j+1]) j++;
        if(j==n)
        {
            printf("%d ",i-j);
            j=ne[j];
        }
    }
    return 0;
}

 参考文献：《算法导论》