回文质数问题

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

• 前言
• 一、pandas是什么？
• 二、使用步骤
  • 1.引入库
  • 2.读入数据
• 总结

---

前言

回文数也就是如：101，121等等数 ，质数也就是只能被本身或者1除的数，以下题目是两者的结合

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、题目

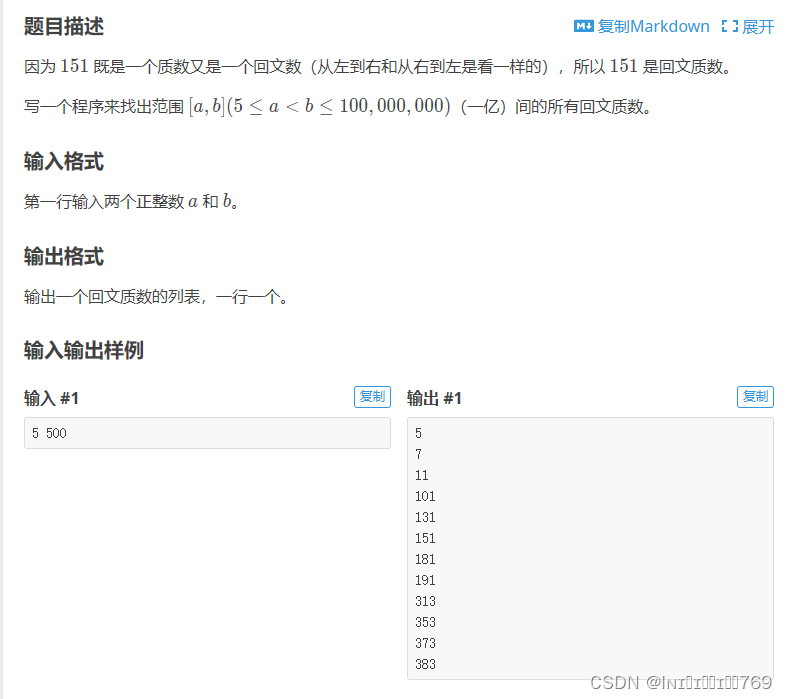
二、方法

1.代码

代码如下（示例）：

#include<bits/stdc++.h>
using namespace std;

bool find(int a){  //判断质数
/*
	 if (a <= 1) {
        return false;
    }
    if (a == 2) {
        return true;
    }
    if (a % 2 == 0) {
        return false;
    }
    int sql=(int )sqrt(1.0*a);
	for(int i=3;i<=sql;i+=2){   //质数肯定是奇数，每次加2
	if(a%i==0)
	return false;
	} 
	return true;
*/ 
	int sql=(int )sqrt(1.0*a);
	for(int i=2;i<=sql;i++){ //2之前的都不是，从2开始就行
		if(a%i==0)
		return false;
	} 
	return true;
}

bool hw(int num) {   //判断回文
    int temp = num;
    int ans = 0;
    while (temp > 0) {
        int digit = temp % 10;
        ans= ans * 10 + digit;
        temp /= 10;
    }
    if (ans==num){
    return true;
}
    else{
    return false;}
}

int main(){
	int  a,b;
	cin>>a>>b;
	if (a < 5) a = 5;
    if(b>=9999999) b=9999999;
	for(int i=a;i<=b;i++){
		if(hw(i)&&find(i))//!!!!hw一定要先判断，再判断find质数
		cout<<i<<endl;
	}
	return 0;
}

补充：sqrt函数用来求给定的平方根，因为要判断一个整数是否是质数，只需要检查它是否能被小于或等于它平方根的整数整除。如果不能，那么它就是质数，因为大于它平方根的因子一定会有对应的小于平方根的因子。sqrt() 函数返回的是 x 的平方根，返回值类型是 double 型，所以我这乘了1.0

回文先判断的原因是先对于先判断质数来说，可以提高代码的性能，排列方式更加高效。

---

总结

以上例题，是回文和质数的结合。