60天python训练计划----day57

DAY 57 经典时序模型1

知识点回顾

1. 序列数据的处理：
   1. 处理非平稳性：n阶差分
   2. 处理季节性：季节性差分
   3. 自回归性无需处理
2. 模型的选择
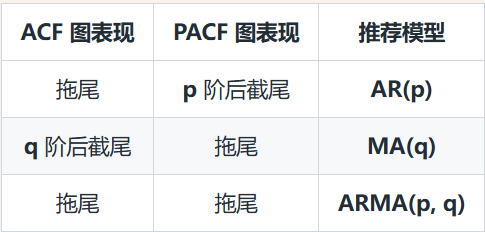
   1. AR(p) 自回归模型：当前值受到过去p个值的影响
   2. MA(q) 移动平均模型：当前值收到短期冲击的影响，且冲击影响随时间衰减
   3. ARMA(p,q) 自回归滑动平均模型：同时存在自回归和冲击影响

昨天说了数据的检验，需要做自相关性检验、平稳性检验、季节性检验。

我们用了三种核心的诊断工具：

1. 自相关性检验 (ACF/PACF图)：检查数据点之间是否存在内在的、延迟的关联。

2. 平稳性检验 (ADF检验)：判断数据的统计特性（如均值、方差）是否随时间改变。

3. 季节性检验 (肉眼观察或季节性分解)：识别数据中是否存在固定的周期性波动。

 

那么如果数据存在某些特性需要如何处理呢？

我们的核心目标是让数据变得平稳。为什么平稳性如此重要？因为绝大多数经典的时间序列模型（比如ARIMA模型）都建立在一个基本假设之上：数据的统计特性是恒定的。如果数据不平稳，就像一个人的脾气阴晴不定，模型就很难抓住其规律，预测自然也就不准了。

我们今天会针对两大“病症”进行处理：非平稳性和季节性。而自相关性，我们则需要换个思路，它不是一个要消除的“病症”，反而是我们要利用的“特征”，我们最后会讲到。

一、序列数据的处理

1.处理非平稳性

        通过昨天的ADF检验，我们发现p值显著大于0.05，这表明数据是非平稳的。通常，这意味着数据存在趋势（Trend），比如股价长期来看在上涨，或者销量逐年递增。

核心疗法：差分 (Differencing)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 设置中文字体，防止matplotlib显示乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成一段非平稳数据（随机游走+趋势）
np.random.seed(42)
# 随机游走部分
random_walk = np.random.randn(500).cumsum() # 累积和生成随机游走
# 添加一个线性趋势
trend = np.linspace(0, 100, 500)
# 合成我们的时序数据
data = pd.Series(random_walk + trend)
data.index = pd.date_range(start='2022-01-01', periods=500)

# 2. 诊断原始数据
plt.figure(figsize=(12, 6))

plt.plot(data)
plt.title('原始数据（有明显趋势）')

        随机游走（Random Walk）是一种数学模型，常用于描述随机过程中的路径变化。在随机游走模型中，每一步的方向和大小都是随机确定的，且与之前的步骤相互独立。这种模型可以用来模拟股票价格、分子运动、赌博结果等具有不确定性的现象。

        上述代码为了合成一个具有趋势性和随机性的时间序列，它结合了随机游走和线性趋势的特征。