动态规划之 0-1 背包问题(进阶一维数组)包含回溯找方案

 

从这个情境导入的例子我们知道 想要通过面试的最大概率是你要保证在有效的时间内得到的考试概率是最大的

由于这个情景不是原子性的,就是这几个算法模块是可以进行拆封的,那么你可以通过计算每个算法模块的价值率来进行计算...

比如你一共只有8天时间,那么我们先对每个算法模块进行换算价值率然后进行降序排列,选中前三个模块花费的天数之后呢,还有2天,这个时候,你可以选择学完二叉树 又或者学两天的排序

但是我们的价值率是每天花费的概率,而且这个一眼就可以看出来是可以进行拆分的,所以我们学2天的排序所得的概率比我们学完二叉树所得的概率要更大,那么也就对应着我们的背包的物品价值更多.

这只是针对上面可以拆分的情景我们可以通过计算价值率来进行合理安排

但是针对于0 -1 背包问题,物品只有一件是不能进行拆封的

 

 

 1.假设在v天内, t(n) > v 说明这个时候的背包容量压根不足以放这个这个物品,此时我们直接跳过这个商品,那么此时 i++ ,但是dp[i][v] = dp[i-1][v],继承上一个状态下

2.假设在v天内 t(n) < v 说明是可以放进去的,对于我们而言是有两种选择:放还是不放

2.1放的话,你这个状态的可用容量是t(n) ,但是你得保证你现在用了t(n) - v,说明你还有v的空间没用,此时你就需要去放这个i商品,占据v容量,然后价值+p(n)

2.2 不放的话,你还是继承上一个状态

这个二维数组就是具体的模拟

 如何根据这个二维数组来进行回溯,找到最大价值的具体方案 

回溯是从后往前来进行回溯的,因为我们最后返回的是dp[商品个数][最大容量]

这个值存储的就是最多的价值,我们从这个地方往上遍历,也就是 10/15这里

你想啊:它的上面是dp[i-1][v],如果我们没选第五件物品,继承的肯定是dp[i - 1 ][v],所有要去判断

dp[i][v] ==   dp[i-1][v] 不相等说明没有继承,也就是选择了i 这件物品,我们先去把编号加到集合中去.

然后i--,看看上一个状态(上一个状态再去比较,可能还是继承)

如果相等呢,也就是继承了上一状态,那么i--,我们不添加,继续去比较上一个状态和上上个状态

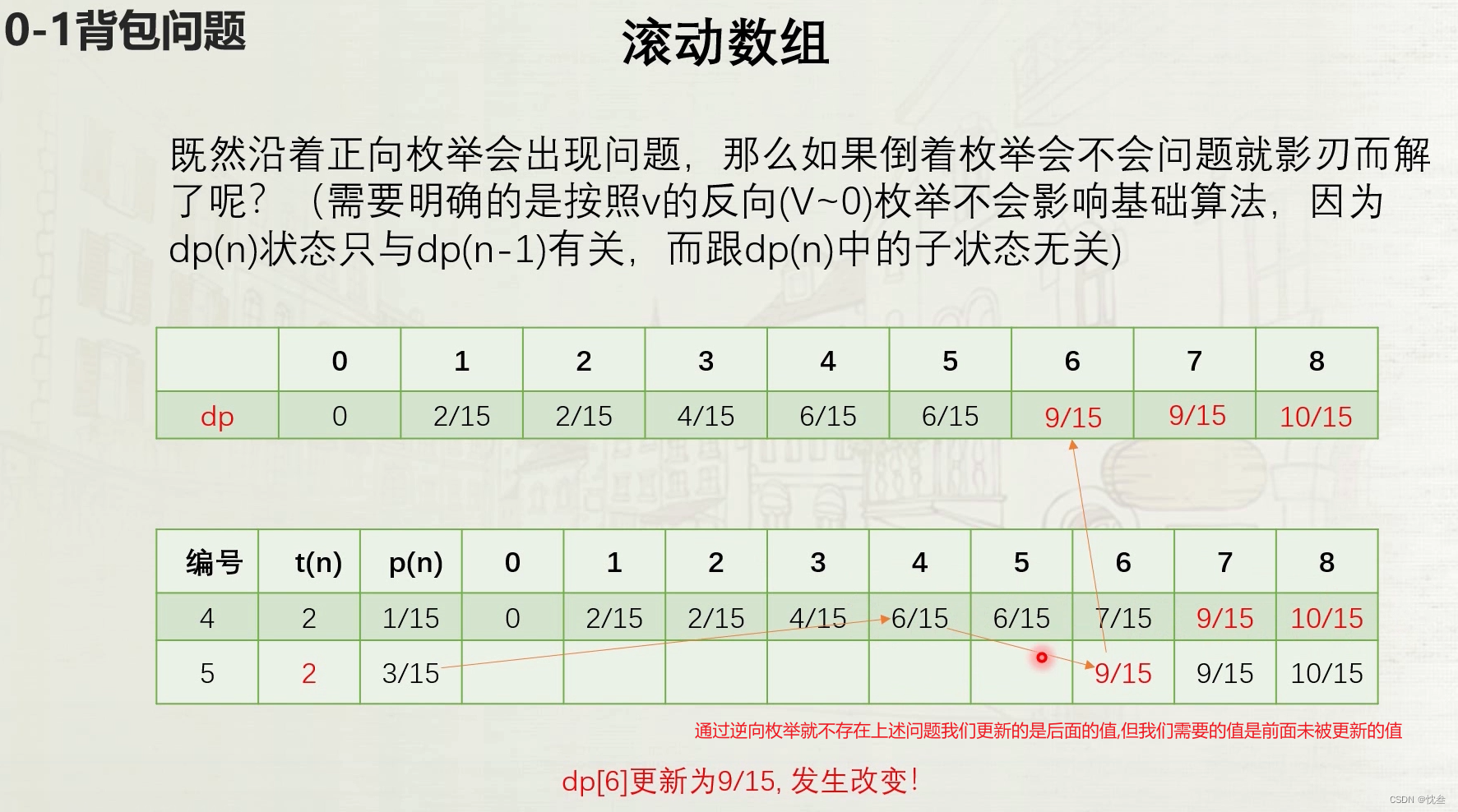
优化:滚动数组 -- 优化的是空间复杂度,因为我们二维数组空间复杂度是 O(VN)

可以简化为一维数组来求得最大价值

 

 

 

 这是一维数组的优化代码 :有一点就是:一维数组其实是无法进行回溯的,上面的回溯我们介绍的很清楚,他是需要对二维数组才能回到上一个状态,所以需要保存所有的状态,那么当我们不需要知道具体方案的时候,就可以用这个优化 

 接下来放的是Java代码:

 

 优化算法:

0-1背包问题扩展: 求正数数组最小不可组成和

求正数数组的最小不可组成和_百度笔试题_牛客网

这道题想要去解还真不容易发现:

首先确定区间长度很简单,确定之后我们要去判断哪个地方最先被检测出来

实际上是这样的, 定义一个布尔类型的数组来表示哪个地方可以被子集和求出来,哪个地方不能被子集和求出来,我们对数组每个位置进行更新再去遍历一下就好了.

那么如何去快速准确的更新这个区间呢???

假设: arr[i] = j   ,再去递推就是 : form[j] = form[j - arr[i] ] ,你想是不是这个道理

假设你遍历到数组的第 i 个位置,此时form[ j - arr[i] ] 他是true ,那么你只需要加上 arr[i] 就可以保证满足条件,当然写代码的时候不需要加上,我们懂那个意思就好了

这一串代码: 每个元素都要去被这个集合判断一下

假设第一个元素 arr[i]    =  3,此时你从max ~ arr[i] 这个范围内

当   j   = 3时候, form[ j  ] = form[ 0 ] = true

然后第二个元素就是 arr[1] = 2

此时 form[ 5- 2 ] = form[ 3 ] = form[ 5 ]  = true,就这样不断的去判断

    public static int getFirstUnFormedNum(int[] arr){
        int min = Integer.MAX_VALUE;
        int max = 0;
        for (int o:
             arr) {
            max+=o;
            min = Math.min(o,min);
        }
        boolean[] form = new boolean[max+1];
        form[0] = true;
        for(int i = 0; i < arr.length;i++){
            for(int j = max; j >= arr[i];j--){
                form[j] = form[j - arr[i]] || form[j];
            }
        }
        for (int i = min; i <=  max ; i++) {
            if(!form[i]){
                return i;
            }
        }
        return max+1;
    }
}