Leetcode 力扣 64.最小路径和

题目描述：

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

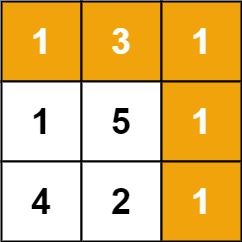
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

解析：很简单的一道动态规划题目。创建一个二维数组，数组中每个元素的值为起点0,0到该点的最短路径，通过循环获得所有的值，最后输出终点的值即可 

代码：（动态规划）

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();

        if(m==n&&m==1) return grid[0][0];
        vector<vector<int>> a(m,vector<int>(n));
        a[0][0]=grid[0][0];
        for(int i=1;i<m;i++){
            a[i][0]=a[i-1][0]+grid[i][0];
        }
        for(int i=1;i<n;i++){
            a[0][i]=a[0][i-1]+grid[0][i];
        }

        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                a[i][j]=min(a[i-1][j],a[i][j-1])+grid[i][j];
            }
        }

        return a[m-1][n-1];
    }
};