数字信号与图像处理实验三：图像处理基础与图像变换_对图像做余弦变换后,并截取图像的主要信息,并做反余弦变换,显示丢失了部分信息的-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_59430424/article/details/128134299

实验三：图像处理基础与图像变换

通过本实验加深对数字图像的理解，熟悉MATLAB中的有关函数；应用DCT对图像进行变换；熟悉图像常见的统计指标，实现图像几何变换的基本方法。

班级	姓名	实验名	完成时间
计算2014	lx	图像处理基础与图像变换	2022.11.30

实验要求：

熟悉MATLAB的图像处理函数
熟练掌握java/C#/C/C++的图像处理方法
完成程序代码编写

1. 选择两幅图像，读入图像并显示，同时使用Matlab计算图像的大小、灰度平均值、协方差矩阵、灰度标准差和相关系数。

%% 读入图像并显示
close all; clear; clc;
I1 = imread('Xi.jpg'); I2 = imread('Mei.jpg');
I1_grey = rgb2gray(I1); I2_grey = rgb2gray(I2);
figure(1); imshow(I1_grey); figure(2); imshow(I2_grey);
% 计算图像大小
size1 = size(I1_grey)
size2 = size(I2_grey)
% 计算灰度平均值
I1_db = double(I1_grey); I2_db = double(I2_grey);
[M1, N1] = size(I1_db); [M2, N2] = size(I2_db);
ave1_grey = sum(sum(I1_db))/(M1*N1)
ave2_grey = sum(sum(I2_db))/(M2*N2)
% 计算协方差矩阵
c1 = cov(I1_db);
c2 = cov(I2_db);
% 计算灰度标准差
s1=std2(I1_db)
s2=std2(I2_db)
J1=histeq(I1_grey);
J2=histeq(I2_grey);
figure;
subplot(221);imshow(I1_grey),title('原图');
subplot(222);imshow(J1),title('直方图均衡化后的图像');
subplot(223);imshow(I2_grey),title('原图');
subplot(224);imshow(J2),title('直方图均衡化后的图像');
% 计算相关系数
[I1_db, I2_db] = size2same(I1_db, I2_db); % 将两幅图像裁剪为相同大小
x = corr2(I1_db, I2_db)

2. DCT变换

RGB = imread('autumn.tif');
I = rgb2gray(RGB);
fugure(1);
Imshow(I);
J = dct2(I);
Figure(2);
imshow(log(abs(J)),[]), colormap(jet(64)), colorbar

观察实验结果，说明figure2中图像色彩变换的规律，并写出其原因。

%对灰度矩阵进行量化
J(abs(J)<0.1)=0; 
I=idct2(J)/255;
figure(), imshow(I), title('经过DCT变换，然后逆变换的灰度图像');

对原始图像进行二维离散余弦变换，如中间频域能量分布图所示，变换后DCT系数能量主要集中在左上角，其余大部分系数接近于零，即大多数能量都集中在了左上角低频处。

图像中，低频分量可以看作是基本图像，高频分量为边缘轮廓细节信息（也可能是噪声）。绝大多数能量都包含了大量平坦区域，因此大部分能量集中于低频区域（左上角），从而可以达到去除空间冗余的目的。（其中，DCT变换尺寸越大，DCT去相关性能越好，但是DCT的计算复杂度会随之增大）

这说明DCT具有适用于图像压缩的特性。将变换后的DCT系数进行门限操作，将小于一定值得系数归零，这就是图像压缩中的量化过程，然后进行逆DCT运算，得到压缩后的图像，如右图。比较变换前后的图像，肉眼很难分辨出有什么区别，可见压缩的效果比较理想。

3. DCT图像压缩

I=imread('cameraman.tif');
I=im2double(I);
T=dctmtx(8);
B=blkproc(I,[8 8],'P1*x*P2',T,T'); % x就是每一个分成的8*8大小的块，P1*x*P2相当于像素块的处理函数，p1=T p2=T’,也就是fun=p1*x*p2'=T*x*T'的功能是进行离散余弦变换
mask=[1 1 1 1 0 0 0 0 
      1 1 1 0 0 0 0 0 
      1 1 0 0 0 0 0 0 
      1 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0];
B2=blkproc(B,[8 8],'P1.*x',mask); % 舍弃每个块中的高频系数，达到图像压缩的目的
I2=blkproc(B2,[8 8],'P1*x*P2',T',T); % 反余弦变换，重构图像
subplot(1,2,1),imshow(I);
subplot(1,2,2),imshow(I2);

3.1 运行代码，观察实验结果，写出图像压缩的基本原理。

运行代码后，结果如下：

3.11

发现右边压缩后的图片相较于原图变得模糊。

上面代码中，首先使用函数dctmtx产生8*8的DCT变换矩阵，然后使用函数blkproc将图像分成8*8的块，P1*x*P2相当于像素块的处理函数，p1=T p2=T’，也就是fun=p1*x*p2'=T*x*T'的功能是对每个像素块进行离散余弦变换，将图像以利用mask掩膜矩阵对其进行量化，保留左上角主要的系数值，对于右下角的值由于其为非常小的高频系数，量化去除后对于图像的质量影响不大，可以利用这一性质对图像进行压缩处理。保留系数越多则图像压缩质量越好。

mask掩膜矩阵主要起屏蔽的作用，用掩膜对图像上某些区域作屏蔽，使其不参加处理或不参加处理参数的计算，或仅对屏蔽区作处理或统计

3.2 计算原图像和压缩后图像的差（相减）

I3 = I - I2;
figure; imshow(I3); title('两图像的差值',fontsize=20);

3.22

3.3 修改mask矩阵中非0元素的个数，写出修改后的压缩的图像和原图像之间的差和非0元素个数的关系，并比较变换后系数的重要性。

close all; clear; clc;
I=imread('cameraman.tif');
I=im2double(I);
T=dctmtx(8);
B=blkproc(I,[8 8],'P1*x*P2',T,T');
mask1=[1 1 1 1 1 0 0 0 
      1 1 1 1 0 0 0 0 
      1 1 1 0 0 0 0 0 
      1 1 0 0 0 0 0 0 
      1 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0];
mask2=[1 1 1 1 0 0 0 0 
      1 1 1 0 0 0 0 0 
      1 1 0 0 0 0 0 0 
      1 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0];
mask3=[1 1 0 0 0 0 0 0 
      1 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0 
      0 0 0 0 0 0 0 0];
B1=blkproc(B,[8 8],'P1.*x',mask1);% 保留15个系数
I1=blkproc(B1,[8 8],'P1*x*P2',T',T);
B2=blkproc(B,[8 8],'P1.*x',mask2);% 保留10个系数
I2=blkproc(B2,[8 8],'P1*x*P2',T',T);
B3=blkproc(B,[8 8],'P1.*x',mask3);% 保留3个系数
I3=blkproc(B3,[8 8],'P1*x*P2',T',T);
subplot(1,4,1),imshow(I); title('原图',fontsize=20);
subplot(1,4,2),imshow(I1); title('15个非0系数',fontsize=20);
subplot(1,4,3),imshow(I2); title('10个非0系数',fontsize=20);
subplot(1,4,4),imshow(I3); title('3个非0系数',fontsize=20);
% 计算原图像和压缩后图像的差
I11 = I - I1;
I22 = I - I2;
I33 = I - I3;
figure; 
subplot(1,3,1); imshow(I11); title('15个非0系数',fontsize=20);
subplot(1,3,2); imshow(I22); title('10个非0系数',fontsize=20);
subplot(1,3,3); imshow(I33); title('3个非0系数',fontsize=20);

3.3

由上图可知，mask中非0系数的数量直接影响了图像压缩后的质量，在非0系数大于10时，压缩后的图像和原始图像差别肉眼观察不出，在只有3个非0系数时，图像失真严重，细节损失最多，可见在非0系数较少（小于10）时，非0系数的个数直接影响了压缩后图像的质量。

由上图可以知道，非0系数越少，压缩前后图像的差越大，并且观察图像可以知道，差值在图像的边缘处更加明显，说明图像压缩对于物体边缘细节的影响最大。

3.4 使用别的图像进行上述实验，验证结论正确与否

3.31

3.32

根据图像分析可知，与上题得出结论相符合。

4. 使用C++与OpenCV实现 3 的图像压缩

本题需在第三问的基础上进行，由于需要使用opencv，所以需要复现matlab中的dctmtx和blkproc函数，以此达到使用DCT变换压缩图像并不损失图像分辨率的效果。

首先查询二维DCT公式：
$F(u,v)=c(u)c(v)\sum_{i=0}^{N-1}{\sum_{j=0}^{N-1}{f(i,j)\cos[\frac{(i+0.5\pi)}{N}u]\cos[\frac{(j+0.5\pi)}{N}u]}}$

$c(u)=\begin{cases} \sqrt{\frac{1}{N}},u=0 \\ \sqrt{\frac{2}{N}},u\neq 0 \end{cases}$

二维DFT其实就是进行两次一维DFT，所以可以用以下更简单的方式实现：
$F=AfA^T$

$A(i,j)=c(i)\cos[\frac{(j+0.5\pi)}{N}i]$

N对应二维矩阵的总行数，i对应二维矩阵此时的行，j对应二维矩阵此时的列，对原图像分出的每一个块，执行公式3

//构造8*8的余弦变换矩阵DCTMat，实现公式4
//... ...

//构造8*8的余弦变换矩阵，实现公式4
for (int i = 0; i < DCTMat.rows; i++)
{
    for (int j = 0; j < DCTMat.cols; j++)
    {
        if (i == 0)
        {
            a = pow(1.0 / DCTMat.rows, 0.5);
        }
        else
        {
            a = pow(2.0 / DCTMat.rows, 0.5);
        }
        q = ((2 * j + 1) * i * M_PI) / (2 * DCTMat.rows);
        DCTMat.at<double>(i, j) = a * cos(q);
    }
}
DCTMatT = DCTMat.t(); // 得到余弦变换转置矩阵
int rNum = doubleImgTmp.rows / 8;
int cNum = doubleImgTmp.cols / 8;
for (int i = 0; i < rNum; i++)
{
    for (int j = 0; j < cNum; j++)
    {
        /*
			RECT(x,y,width,height)
			x：左上角的列坐标
			y：左上角的行坐标
			width：裁剪几列
			height：裁剪几行
			*/
        ROIMat = doubleImgTmp(Rect(j * 8, i * 8, 8, 8)); //裁剪出8*8的块
        ROIMat = DCTMat * ROIMat * DCTMatT;	//T*x*T'，公式3
    }
}

这里的ROIMat矩阵，就相当于是一个滑块，每次取出图像中的一个8*8的块，然后对这个块进行离散余弦变换，块的执行顺序如下图：

其实这一步让我联想到了机器学习中的卷积层，卷积层是由一组滤波器组成，滤波器其实就可以理解为这里的8*8的DCT变换矩阵，然后进行如下操作：

在图像的某个位置上覆盖滤波器；
将滤波器中的值与图像中的对应像素的值相乘；
把上面的乘积加起来，得到的和是输出图像中目标像素的值；
对图像的所有位置重复此操作。

接着需要复现掩码矩阵对DCT变换后的图像进行区域编码处理，舍弃高频系数，达到图像压缩，这里也需要对图像分块处理。首先构造mask掩码矩阵，将其左上角赋值为1，其余部分赋值为0，然后将掩码矩阵与图像上每个块做点乘，达到舍弃高频系数的作用。

void regionalCoding(Mat doubleImgTmp, int retain)
{
	int rNum = doubleImgTmp.rows / 8;
	int cNum = doubleImgTmp.cols / 8;
	//分块处理
	Mat winMat = Mat(8, 8, CV_64FC1);
	Mat mask = Mat::ones(8, 8, CV_64FC1);
	for (int r = 0; r < 8; r++) {
		for (int c = 0; c < 8; c++) {
			//8*8块中，保留左上角retain * retain的上三角区域
			if (r + c > retain - 1) {
				mask.at<double>(r, c) = 0.0;
			}
		}
	}
	for (int i = 0; i < rNum; i++)
	{
		for (int j = 0; j < cNum; j++)
		{
			winMat = doubleImgTmp(Rect(j * 8, i * 8, 8, 8));
			winMat = winMat.mul(mask);  //与掩码矩阵做点乘，舍弃高频系数
		}
	}
	doubleImgTmp.convertTo(doubleImgTmp, CV_8U); // CV_8U: 8位无符号整数
}

接着就只需要将进行掩码操作后的矩阵进行复原，即DCT逆变换，与DCT变换操作一致，这里就不放代码了，在操作完成后，就得到了压缩后的图像。

压缩后的大小和原图对比：

查看分辨率：

由此，可以发现压缩后的图像在没有改变分辨率的情况下，压缩了画质，并且只减少了细节部分，整体图像仍可以分辨出。但是问题4到此没有结束，在之前的图片中，细心的读者会发现图片有不完整的块，这里我选择对不完整的块做填充操作，参考blkproc官方文档：

我选择采用replicate操作进行块填充，为了讲解更清楚，另外作图，图像右边和下边会有未被处理的块，如下：

以14*13的图片为例算法分块时发现只能分出一个块，剩下的区域需要做填充，如下：

将最外层的边缘复制给边缘的不完整块，代码实现如下：

//获得行方向和列方向的块数，向下取整，不完整的块做"replicate"填充处理
	int rNum = doubleImgTmp.rows / 8;
	int cNum = doubleImgTmp.cols / 8;
	int row = doubleImgTmp.rows;
	int col = doubleImgTmp.cols;
	if (row % 8 != 0 || col % 8 != 0) {
		rNum++;
		cNum++;
		ImgTmp = Mat(rNum * 8, cNum * 8, CV_64FC1);
		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				ImgTmp.at<double>(i, j) = doubleImgTmp.at<double>(i, j);
			}
		}
		for (int i = 0; i < rNum * 8; i++) {
			for (int j = (cNum - 1) * 8; j < cNum * 8; j++) {
				ImgTmp.at<double>(i, j) = ImgTmp.at<double>(i, j - 1);
			}
		}    
		for (int i = (rNum - 1) * 8; i < rNum * 8; i++) {
			for (int j = 0; j < cNum * 8; j++) {
				ImgTmp.at<double>(i, j) = ImgTmp.at<double>(i - 1, j);
			}
		}
	}

当然，如果就这样结束了，那么图像的分辨率就被我们人为改变了，如下：

由于进行了填充操作，导致图像分辨率强行扩充到了8的倍数，破坏了原始图像。

所以我们需要在图像做完DCT逆变换后，将其恢复到原始的分辨率：

Mat rehabilitation(Mat doubleImgTmp, int rows, int cols) {
	Mat reha = Mat(rows, cols, CV_64FC1);
	for (int i = 0; i < rows; i++) {
		for (int j = 0; j < cols; j++) {
			reha.at<double>(i, j) = doubleImgTmp.at<double>(i, j);
		}
	}
	return reha;
}

至此，代码部分的编写就结束了，我们试着将第一题的图片放入其中测试：

压缩后的大小和原图对比：

可以看到，在保留了大部分图像信息的同时，图像大小被我们减少了一半。

查看分辨率

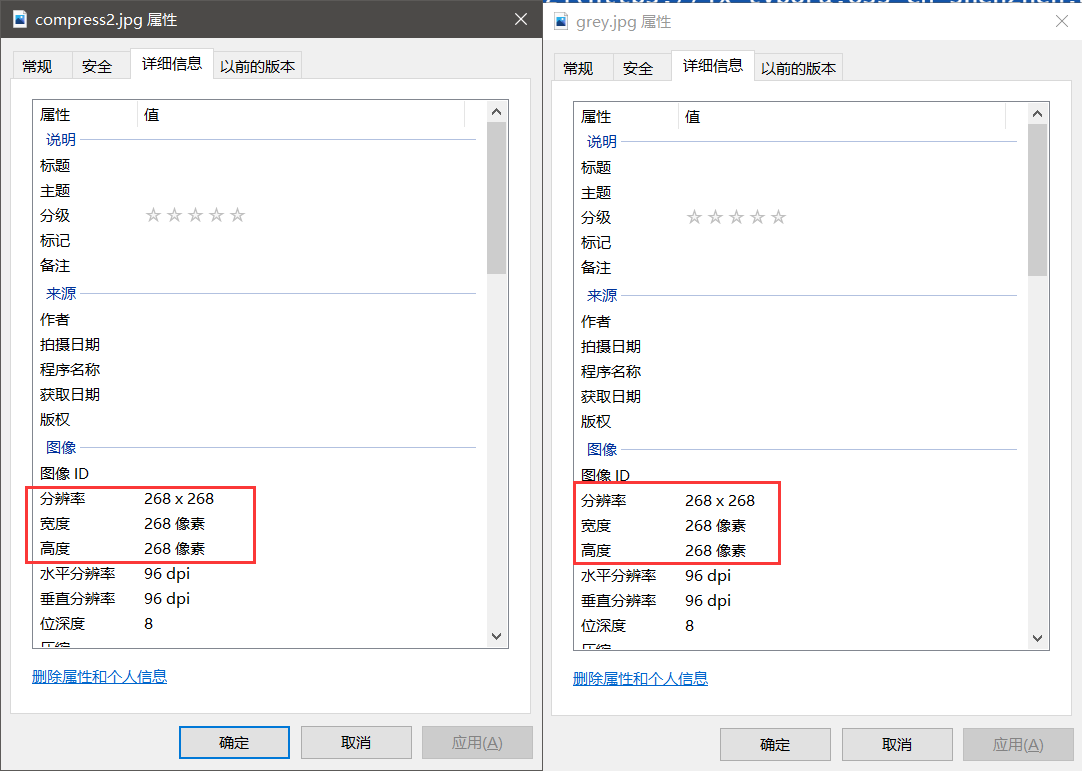
图像的分辨率没有改变，至此，代码编写完毕。

5. 编写程序实现图像的水平垂直和中心对称（注:不能用系统的旋转函数）

其实水平对称、垂直对称和中心对称的操作都比较类似，运用矩阵中坐标的对称性，将原图赋值给另一张新的图。

#include <opencv2/opencv.hpp>
using namespace cv;

int main()
{
	/*载入图像并显示*/
	Mat img = imread("...", 0);
	Mat newImg = Mat::zeros(img.rows, img.cols, CV_8UC1);
	imshow("原图", img);

	//flag = 1, 水平对称
	//flag = 2, 垂直对称
	//flag = 3, 中心对称
	int flag = 2;

	/*对称处理*/
	for (int i = 0; i < img.rows; i++)
	{
		for (int j = 0; j < img.cols; j++)
		{
			if (flag == 1) {
				newImg.at<uchar>(i, j) = img.at<uchar>(i, img.cols - j - 1);
			}
			else if (flag == 2) {
				newImg.at<uchar>(i, j) = img.at<uchar>(img.cols - i - 1, j);
			}
			else if (flag == 3) {
				newImg.at<uchar>(i, j) = img.at<uchar>(img.cols - i - 1, img.cols - j - 1);
			}
			else {
				printf("请重新输入flag！");
			}
		}
	}

	imshow("效果图", newImg);
	waitKey(0);
	imwrite("...", newImg);
	return 0;
}

这一部分比较简单，其实就是将图片（也就是二维矩阵）沿着某条线或某个点，把坐标相互颠倒一下。

总结

在本次实验中，主要深入学习了对图像的操作，基本操作比如读入、显示、计算图像大小、灰度平均值等，高级操作比如图像压缩、对称等操作。通过本次实验，对于DCT变换的理解更加深刻，对于图像的操作也更加熟练。

在实验中遇到了许多问题，比如在第一问中，一开始没有将图像转为灰度图，导致在求协方差矩阵时一直出错（matlab自带的函数conv()只能计算二维矩阵的协方差矩阵，RGB图像为三维矩阵）。在做DCT变换时，一开始不理解mask矩阵中的非0系数，后来发现mask矩阵可以理解为一个筛网，将0的部分给舍弃，将1的部分保留下来，原图被分成了8*8的64个块，每个块都对应了mask矩阵上的一个元素。在第四问时，在VS2017上配置OpenCV花费了我不少时间，具体的配置过程参考了这篇博客(36条消息) VS2017配置opencv教程（超详细！！！）_King_LJames的博客-优快云博客_opencv。

重点是第四问，一开始，我并没有按照老师第三题的算法去做，而是很敷衍地直接改分辨率达到压缩图像大小的效果，然后答辩的时候才知道是错的，需要使用DCT变换去做图像压缩，也就是复现第三题中的算法，于是开始使用opencv复现，其中遇到了很多问题，整体的难度也比之前的做法难了很多。我首先去查了DCT变换的公式，然后手写函数实现，然后需要使用掩码矩阵对原图像做区域编码，最后使用DCT逆变换恢复原始图像，在完成上述步骤后，我发现使用自己的图片做压缩会出错，因为不是每张图片都可以正好分成8*8块，于是又去查官方blkproc函数的[文档]图像的非重复块处理 - MATLAB blockproc - MathWorks 中国，发现确实有填充不完整快的超参数，于是模仿了replicate方式，写了算法去做边缘重复填充，然后老师又指出问题，没有将分辨率复原，于是又复工。第四问的代码参考了博客(36条消息) OpenCV 区域编码和阈值编码实现图像压缩（8*8DCT变换，保留50%的系数）_morning_sun_lee的博客-优快云博客。

总的来说，这次实验收获很多，老师真的也很负责任地指出了我的问题，从态度到学术上都给予了一定的批评和指正，希望自己能一直以严谨认真的态度对待之后每一次任务。

附（第四问代码）

头文件 compress.h:

#define _USE_MATH_DEFINES
#include <iostream>
#include <math.h>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;


//功能等同于Matlab的blkproc函数（blkproc(I,[8 8],'P1*x*P2',g,g')），用于对图像做8*8分块DCT
Mat blkproc_DCT(Mat doubleImgTmp);
//功能等同于Matlab的blkproc函数（blkproc(I,[8 8],'P1*x*P2',g',g)），用于做8*8分块DCT逆变换，恢复原始图像
Mat blkproc_IDCT(Mat doubleImgTmp, int flag, int rows, int cols);
//区域编码函数，功能等同于Matlab的blkproc函数（blkproc(I1,[8 8],'P1.*x',a)）
void regionalCoding(Mat doubleImgTmp, int retain);
//将图像恢复成原始分辨率
Mat rehabilitation(Mat doubleImgTmp, int rows, int cols);


Mat blkproc_DCT(Mat doubleImgTmp)
{
	Mat ucharImgTmp;
	Mat DCTMat = Mat(8, 8, CV_64FC1);	//用于DCT变换的8*8的余弦变换矩阵
	Mat DCTMatT;	//DCTMat矩阵的转置
	Mat ROIMat = Mat(8, 8, CV_64FC1);	//用于分块处理的时候在原图像上面移动
	double a = 0, q;	//DCT变换的系数

	//构造8*8的余弦变换矩阵
	for (int i = 0; i < DCTMat.rows; i++)
	{
		for (int j = 0; j < DCTMat.cols; j++)
		{
			if (i == 0)
			{
				a = pow(1.0 / DCTMat.rows, 0.5);
			}
			else
			{
				a = pow(2.0 / DCTMat.rows, 0.5);
			}
			q = ((2 * j + 1) * i * M_PI) / (2 * DCTMat.rows);
			DCTMat.at<double>(i, j) = a * cos(q);
		}
	}
	DCTMatT = DCTMat.t(); // 得到余弦变换转置矩阵

	//ROIMat在doubleImgTmp以8为步长移动，达到与Matlab中的分块处理函数blkproc相同的效果
	Mat ImgTmp;
	//获得行方向和列方向的块数，向下取整，不完整的块做"replicate"填充处理
	int rNum = doubleImgTmp.rows / 8;
	int cNum = doubleImgTmp.cols / 8;
	int row = doubleImgTmp.rows;
	int col = doubleImgTmp.cols;
	if (row % 8 != 0 || col % 8 != 0) {
		rNum++;
		cNum++;
		ImgTmp = Mat(rNum * 8, cNum * 8, CV_64FC1);
		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				ImgTmp.at<double>(i, j) = doubleImgTmp.at<double>(i, j);
			}
		}
		for (int i = 0; i < rNum * 8; i++) {
			for (int j = (cNum - 1) * 8; j < cNum * 8; j++) {
				ImgTmp.at<double>(i, j) = ImgTmp.at<double>(i, j - 1);
			}
		}
		for (int i = (rNum - 1) * 8; i < rNum * 8; i++) {
			for (int j = 0; j < cNum * 8; j++) {
				ImgTmp.at<double>(i, j) = ImgTmp.at<double>(i - 1, j);
			}
		}
	}
	else ImgTmp = doubleImgTmp.clone();

	for (int i = 0; i < rNum; i++)
	{
		for (int j = 0; j < cNum; j++)
		{
			/*
			RECT(x,y,width,height)
			x：左上角的列坐标
			y：左上角的行坐标
			width：裁剪几列
			height：裁剪几行
			*/
			ROIMat = ImgTmp(Rect(j * 8, i * 8, 8, 8)); //裁剪出8*8的块
			ROIMat = DCTMat * ROIMat * DCTMatT;	//T*x*T'
		}
	}
	ImgTmp.convertTo(ucharImgTmp, CV_8U);
	return ImgTmp;
}

Mat blkproc_IDCT(Mat doubleImgTmp, int flag, int rows, int cols)
{
	//与blkproc_DCT几乎一样，唯一的差别在于：ROIMat = DCTMatT*ROIMat*DCTMat
	//（转置矩阵DCTMatT和DCTMat交换了位置）
	Mat ImgTmp;
	//64FC1代表每一个像素点元素占64位浮点数，通道数为1
	Mat DCTMat = Mat(8, 8, CV_64FC1); 
	Mat DCTMatT;
	Mat ROIMat = Mat(8, 8, CV_64FC1);
	double a = 0, q;
	for (int i = 0; i < DCTMat.rows; i++)
	{
		for (int j = 0; j < DCTMat.cols; j++)
		{
			if (i == 0)
			{
				a = pow(1.0 / DCTMat.rows, 0.5);
			}
			else
			{
				a = pow(2.0 / DCTMat.rows, 0.5);
			}
			q = ((2 * j + 1) * i * M_PI) / (2 * DCTMat.rows);
			DCTMat.at<double>(i, j) = a * cos(q);
		}
	}

	DCTMatT = DCTMat.t();
	int rNum = doubleImgTmp.rows / 8;
	int cNum = doubleImgTmp.cols / 8;
	for (int i = 0; i < rNum; i++)
	{
		for (int j = 0; j < cNum; j++)
		{
			ROIMat = doubleImgTmp(Rect(j * 8, i * 8, 8, 8));
			ROIMat = DCTMatT * ROIMat * DCTMat;
		}
	}
	if (flag) {
		Mat reha = rehabilitation(doubleImgTmp, rows, cols);
		reha.convertTo(ImgTmp, CV_8U);
	}
	else doubleImgTmp.convertTo(ImgTmp, CV_8U);
	return ImgTmp;
}

void regionalCoding(Mat doubleImgTmp, int retain)
{
	int rNum = doubleImgTmp.rows / 8;
	int cNum = doubleImgTmp.cols / 8;
	//分块处理
	Mat winMat = Mat(8, 8, CV_64FC1);
	Mat mask = Mat::ones(8, 8, CV_64FC1);
	for (int r = 0; r < 8; r++) {
		for (int c = 0; c < 8; c++) {
			//8*8块中，保留左上角retain * retain的上三角区域
			if (r + c > retain - 1) {
				mask.at<double>(r, c) = 0.0;
			}
		}
	}
	for (int i = 0; i < rNum; i++)
	{
		for (int j = 0; j < cNum; j++)
		{
			winMat = doubleImgTmp(Rect(j * 8, i * 8, 8, 8));
			winMat = winMat.mul(mask); //与掩码矩阵做点乘，舍弃高频系数
		}
	}
	doubleImgTmp.convertTo(doubleImgTmp, CV_8U); // CV_8U: 8位无符号整数
}

Mat rehabilitation(Mat doubleImgTmp, int rows, int cols) {
	Mat reha = Mat(rows, cols, CV_64FC1);
	for (int i = 0; i < rows; i++) {
		for (int j = 0; j < cols; j++) {
			reha.at<double>(i, j) = doubleImgTmp.at<double>(i, j);
		}
	}
	return reha;
}

main:

#include "compress.h"

int main()
{
	//以灰度图的形式读入原始的图像
	Mat OriImg = imread("读取路径", 0);
	imshow("srcImg", OriImg);
	int flag = 0; //判断图像是否需要做填充
	if (OriImg.rows % 8 || OriImg.cols % 8) {
		flag = 1;
	}
	Mat doubleImg;
	//将原始图像转换成double类型的图像，方便后面的8*8分块DCT变换
	OriImg.convertTo(doubleImg, CV_64F);

	//对原图片做8*8分块DCT变换
	Mat ImagDCT = blkproc_DCT(doubleImg);

	/*需要注意MAT数据结构在进行函数调用时，
	传值或传引用都会改变实参，因为传值时，
	只将MAT结构体复制了一份，并没有拷贝图像的内存信息，
	操作仍是在同一内存中进行的*/

	//对DCT变换后的系数进行区域编码，舍弃
	regionalCoding(ImagDCT, 4);
	//进行逆DCT变换
	Mat ImgIDCT = blkproc_IDCT(ImagDCT, flag, OriImg.rows, OriImg.cols);
	imshow("compress", ImgIDCT);
	imwrite("目标路径", ImgIDCT);
	waitKey(0);
}