numpy 广播_二维array 广播机制 python-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_59131972/article/details/135431467

本文详细解释了Python中的numpy数组广播机制，包括一维、二维和三维数组的广播示例，以及广播规则：当数组在某些维度上长度不同时，只要有一个长度为1，即可通过广播扩展至相同长度进行操作。最后强调了维度相同和长度不同时的广播要求。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

现在有两个数组分别为：

arr1 = [0, 1, 2, 3, 4, 5, 6]

arr2 = [1]

这两个数组可以进行广播吗？

二维数组广播：

arr1 = np.arange(0,3).reshape(1,3)
array([[0, 1, 2]])
arr2 = np.arange(4,7).reshape(3,1)
array([[4],
       [5],
       [6]])

这两个数组可以进行广播吗？

这两个三维数组可以进行广播吗？

array4 = np.array(np.arange(4).reshape(2,2,1))
      [[[0],
        [1]],

       [[2],
        [3]]]
array5 = np.array(np.arange(12).reshape(2, 1, 6))
[[[ 0,  1,  2,  3,  4,  5]],

       [[ 6,  7,  8,  9, 10, 11]]]

显然可以这是为什么？

我们再看两个数组，它们之间可以通过广播操作，进行计算吗？

我们先看看这段话：

当两个或多个数组在某个维度上的长度不相等时，如果其中至少有一个数组在这个维度上的长度为1，则它们可以进行广播运算。

array5 = np.array(np.arange(24).reshape(2, 2, 6))

[[[ 0,  1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10, 11]],

       [[12, 13, 14, 15, 16, 17],
        [18, 19, 20, 21, 22, 23]]]

array6 = np.array(np.arange(6,14).reshape(2, 1, 4))

[[[ 6,  7,  8,  9]],

       [[10, 11, 12, 13]]]

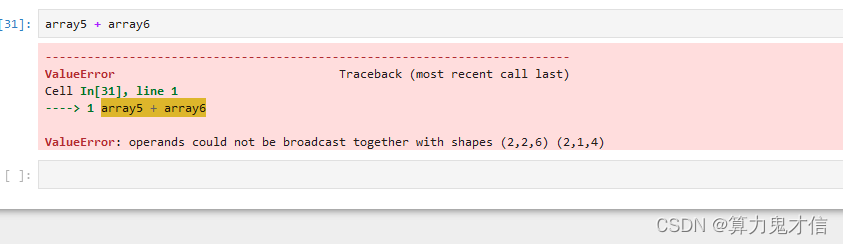
显然不行？这是为什么？看看报错：

ValueError: operands could not be broadcast together with shapes (2,2,6) (2,1,4)

我们来讲讲吧？首先我给大家举例的都是？维度相同相同的数组，两个进行相加的数组的维度都相同，维度不相通的数组我们在后面举例，以维度相同的数组先开始.

先看这两个数组， arr1 = [0, 1, 2, 3, 4, 5, 6] 和 arr2 = [1] arr1 和 arr2 都是一位数组，而且  arr2 一维的长度只有 1 ，所以在它们之间进行操作时，arr2 可以进行扩展延伸至另一方在该维度上相同的长度。

arr2 = [1] 进行广播后 arr2 = [1, 1, 1, 1, 1, 1, 1 ]，然后利用 [1, 1, 1, 1, 1, 1, 1 ] 和[0, 1, 2, 3, 4, 5, 6] 进行求和操作。

我们看看结果是不是我们想的那样？

这两个二维数组是怎样完成的呢？

arr1 = np.arange(0,3).reshape(1,3)

arr2 = np.arange(4,7).reshape(3,1)

arr1 和 arr2 都是2维数组， arr1 数组形状是|（1，3） arr2 的数组形状是 (3,1)请看这段话：

两个数组在所有维度上的长度要么相等，要么其中一个数组在对应维度的长度为1

当两个相同维度的数组上，出现一个维度的长度不相等时，若其中任一数组在该维度上的长度为1，则可以进行广播。

arr1 怎么扩展延伸： arr1 数组在第一个维度上与arr2 不相同，但因长度为1 所以可以进行扩展，扩展到什么程度呢？长度为1的维度就可以被“延伸到”以匹配另一个数组在该维度上的长度，从而实现广播。

arr1 原数组： arr2 原数组

[[0, 1, 2]]                                    [[4],
                                                [5],
                                                [6]]

arr1 广播后的数组 arr2 广播后的数组

[[0, 1, 2], [[4,4,4],

[0, 1, 2] , [5,5,5],

[0, 1, 2]] [6,6,6] ]

然后对扩展后的数组做操作（对应位置的元素进行求和）：

大家计算一下是不是没有问题。

三维数组也是这样玩的，但是需要大家自己主动思考我把运行数组打印给大家，大家思考如何扩展，如何求和？

array5 = np.array(np.arange(8,12).reshape(2, 2, 1))
array6 = np.array(np.arange(6,18).reshape(2, 1, 6 ))

也很简单：大家看相同维度的数组元素个数与排布，三维数组肯定只有三维以下数组，也即是两维和一维存在元素，四维肯定是四维以下，三维、二维、一维数组存在元素，更高维，同理。

现在这是三维，我们去看两个二维数组的元素个数和排布：

行和列分别指的是第二个维度和第三个维度，这是正确的示意，我为了大家和我理解将其解释为了红色子标注。

前提是数组维度相同，在相同维度的地方，有一个数组的维度长度为1，这一个维度长度为1 的维度长度，会扩展到与另一个数组维度长度相同的长度。

什么意思？ arr5 二维数组的地方，是两行一列，它就会通过广播，将列扩展到和arr6列的长度七一样大小的长度，也是七列

arr6二维数组的地方的长度，一行七列，它会通过广播，将行扩展到与arr5 行一样大小 2 的长度，也是 2行。

到时候，arr5 和 arr6 都是两行七列，这就回到了，相同数组进行求和操作。它们分别通过广播完成。

那维度不相同的两个数组怎么通过广播进行加法操作

前提是它们满足以下条件：

所有参与运算的数组在每个对应的维度上的长度要么相同，要么其中至少有一个数组在该维度上的长度为1。
在长度为1的维度上，这个维度将被“拉伸”以匹配其他数组的相应维度。

# 三维数组

arr1 = np.arange(0,9).reshape(3,1,3)
      [[[0, 1, 2]],

       [[3, 4, 5]],

       [[6, 7, 8]]]   
# 二维数组

arr2 = np.arange(6,9).reshape(1,3)
[[6, 7, 8]]

注意：这句话所有参与运算的数组在每个对应的维度上的长度要么相同

arr1 的形状是 (3,1,3) 第一个维度长度是： 3 ，第二个维度长度是： 1，第三个维度长度是： 3

arr2 的形状是（1，3）第一个维度长度是: 1, 第二个维度长度： 3，

啊？它们对应的维度的长度不相同啊？不要忘了 arr1 是三维数组，它里面的二维的第一个维度的长度是：1，第二个维度长度是： 3，这样不就对应了。

因为arr2 的是二维，它如何变成三维，给他再加上一个方向，他就变成了三维，二维数组是一张表格，在深度上加一个方向，也就是再给一些表格让其垒起来。那我们再去看ndarray 数组结构是怎样表示

arr2 ：

[[6, 7, 8]]

arr2变三维：

[

[[6, 7, 8]]

]

给它外层加了一个括号。

我们对比一下arr 变成三维后和三维数组arr1的区别：

arr1：
[[[0, 1, 2]],

  [[3, 4, 5]],

  [[6, 7, 8]]]
是不是将arr2 多给两个，它们的维度、维度长度都相同了。

[

[[6, 7, 8]]，

[[6, 7, 8]]，

[[6, 7, 8]]

]