Python-LBM(格子玻尔兹曼)程序源码实例分析—圆柱绕流篇

最新推荐文章于 2025-03-14 15:31:03 发布

weixin_58913471

最新推荐文章于 2025-03-14 15:31:03 发布

阅读量1.4w

点赞数 34

文章标签： python 流体力学

本文链接：https://blog.youkuaiyun.com/weixin_58913471/article/details/117561995

版权

初次学习LBM计算方法，找到一个比较优秀的用python语言编写的圆柱绕流的实例，对每段代码详细添加了注释，帮助自己总结，也为初学的朋友们提供一点帮助（全部代码在文章最后）。

先放一张结果图像：

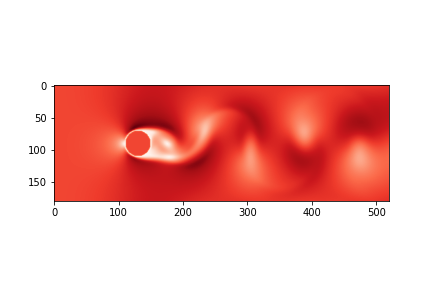
1、导入模块，只需要两个

from numpy import *
from numpy.linalg import *
import matplotlib.pyplot as plt
from matplotlib import cm

2、定义LBM程序所需要的变量：

maxIter = 200000 #总计算次数
Re      = 100.0  #模型要模拟的雷诺数
nx = 520         #模型x轴长度
ny = 180         #模型y轴长度
ly=ny-1.0        #稍后用于计算入口速度，为模型增加扰动，因为当雷诺数较小时，计算缺少扰动。
q = 9            #本文选择的时D2Q9模型
cx = nx/4        #圆柱圆心x坐标
cy=ny/2          #圆柱圆心y坐标
r=ny/9           #圆柱半径长度
uLB = 0.04       #模型的入口速度
nulb=uLB*r/Re    #模型流体的粘性系数，（这里用的是半径，严格来说应该用直径）
omega = 1.0 / (3.*nulb+0.5)  #LBGK(单松弛模型)的弛豫时间

需要有一点注意的就是弛豫时间（有的说松弛时间，我也不确定）的计算，在LBM中模拟流动问题，只需要控制雷诺数相同即可。

雷诺数为：

$Re=\frac{UD}{v}$

在圆柱绕流中U表示入口平均速度，D表示圆柱的直径，v（代码中的nulb）表示流体粘性系数

在LBGK中流体粘性系数和松弛时间的关系则是：

$\tau =\frac{c^{2}}{3}\left ( v-0.5 \right )dt$

其中 $\tau$ 代表松弛时间，c代表格子速度（dx/dt），v代表粘性系数，dt表示时间步长

通过这两个公式就可以将速度、雷诺数、粘性系数和松弛时间联系起来，方便以后模型参数灵活调控。

3、定义分布函数、格子方向等变量

#c代表格子速度，形状为（9，2），9代表有9个方向，2分别代表x,y方向，具体参加示意图
c = array([(x,y) for x in [0,-1,1] for y in [0,-1,1]])

#t代表权重系数，N-S方程的权重系数有三个取值：1/36，1/9，4/9
t = 1./36. * ones(q)            
t[asarray([norm(ci)<1.1 for ci in c])] = 1./9.
t[0] = 4./9.

#noslip为格子速度的反方向
noslip = [c.tolist().index((-c[i]).tolist()) for i in range(q)] 

#i1为6，7，8方向，用于出口边界（右边界）边界处理
i1 = arange(q)[asarray([ci[0]<0  for ci in c])] # Unknown on right wall.

#i2为0，1，2方向，用于入口边界（左边界）边界处理
i2 = arange(q)[asarray([ci[0]==0 for ci in c])] # Vertical middle.

#i3为3，4，5方向，用于入口边界（左边界）边界处理
i3 = arange(q)[asarray([ci[0]>0  for ci in c])] # Unknown on left wall.

本算例中的格子方向的编号和一般情况有所不同：