考研数据结构——C语言实现二叉树和前，中，后，层序遍历

1. 二叉树结构定义：定义了一个名为 BTree 的结构体，它包含一个整型值 value 和两个指向其子树的指针 LeftChild 和 RightChild。

2. 节点访问函数：visit 函数用于输出节点的值，即打印整数值。

3. 节点创建函数：createNode 函数用于动态分配内存以创建一个新的二叉树节点，并初始化其值和子树指针。

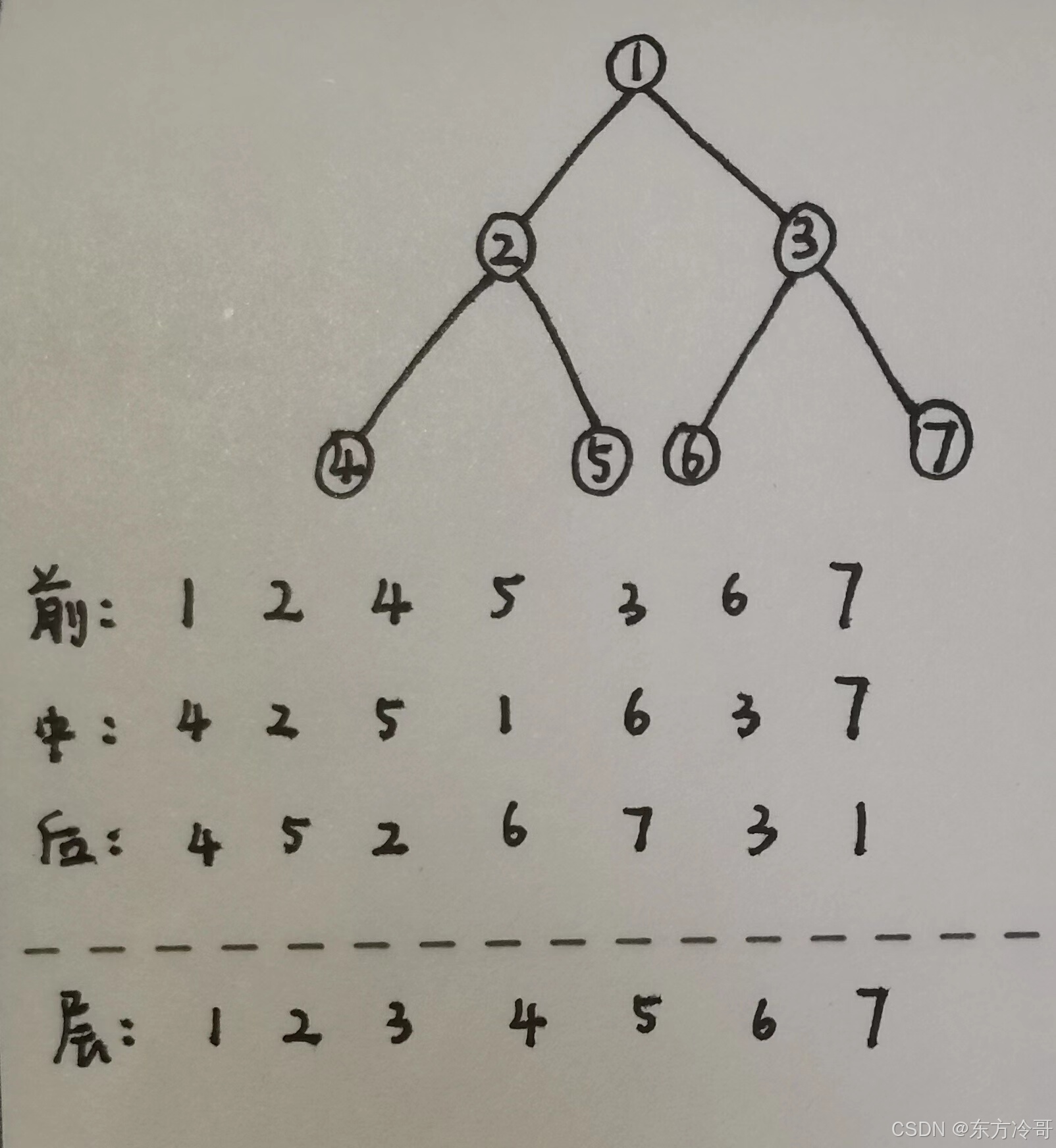
4. 二叉树遍历函数：

   • 前序遍历 (preorderTraversal)：先访问根节点，然后递归地遍历左子树，最后递归地遍历右子树。
   • 中序遍历 (inorderTraversal)：先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。
   • 后序遍历 (postorderTraversal)：先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。

5. 队列结构和操作：为了实现层序遍历，定义了一个队列结构 Queue 和相关的操作函数，包括初始化队列 (initQueue)、检查队列是否为空 (IsEmpty)、入队 (EnQueue) 和出队 (DeQueue)。

6. 层序遍历函数：LevelOrder 函数使用队列来实现层序遍历，即按照从上到下、从左到右的顺序访问二叉树的节点。

7. 主函数 (main)：在主函数中，创建了一个简单的二叉树，并调用了前序、中序、后序和层序遍历函数来展示遍历的结果。最后，主函数应该包含释放二叉树节点所占用内存的代码，但在这段代码中并未实现。

#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;

typedef struct BTree{
	ElemType value;
	BTree* LeftChild;
	BTree* RightChild;
}BTree;

// 访问节点的函数
void visit(ElemType value) {
	printf("%d ", value);
}

// 创建新节点
BTree* createNode(ElemType value) {
	BTree* newNode = (BTree*)malloc(sizeof(BTree));
	if (newNode == NULL) {
		printf("Memory allocation failed!\n");
		exit(1);
	}
	newNode->value = value;
	newNode->LeftChild = NULL;
	newNode->RightChild = NULL;
	return newNode;
}

//前
void preorderTraversal(BTree* root) {
	if (root == NULL) 
		return;
	visit(root->value);
	preorderTraversal(root->LeftChild);
	preorderTraversal(root->RightChild);
}

//中
void inorderTraversal(BTree* root) {
	if (root == NULL) 
		return;
	inorderTraversal(root->LeftChild);
	visit(root->value);
	inorderTraversal(root->RightChild);
}

//后
void postorderTraversal(BTree* root) {
	if (root == NULL)
		return;
	postorderTraversal(root->LeftChild);
	postorderTraversal(root->RightChild);
	visit(root->value);
}

// 队列相关函数的声明
typedef struct Queue {
	BTree* elements[100]; // 假设队列最大长度为100
	int front;
	int rear;
} Queue;

void initQueue(Queue* Q) {
	Q->front = 0;
	Q->rear = 0;
}

int IsEmpty(Queue Q) {
	return Q.front == Q.rear;
}

void EnQueue(Queue* Q, BTree* p) {
	if ((Q->rear + 1) % 100 == Q->front) {
		printf("Queue is full!\n");
		return;
	}
	Q->elements[Q->rear] = p;
	Q->rear = (Q->rear + 1) % 100;
}

void DeQueue(Queue* Q, BTree** p) {
	if (IsEmpty(*Q)) {
		printf("Queue is empty!\n");
		return;
	}
	*p = Q->elements[Q->front];
	Q->front = (Q->front + 1) % 100;
}

//层
void LevelOrder(BTree* T) {
	if (T == NULL)
		return;
	Queue Q;
	initQueue(&Q);
	EnQueue(&Q, T);
	while (!IsEmpty(Q)) {
		BTree* p;
		DeQueue(&Q, &p);
		visit(p->value);
		if (p->LeftChild != NULL)
			EnQueue(&Q, p->LeftChild);
		if (p->RightChild != NULL)
			EnQueue(&Q, p->RightChild);
	}
}

int main() {
	// 创建一个简单的二叉树进行测试
	BTree* root = createNode(1);
	root->LeftChild = createNode(2);
	root->RightChild = createNode(3);
	root->LeftChild->LeftChild = createNode(4);
	root->LeftChild->RightChild = createNode(5);
	root->RightChild->LeftChild = createNode(6);
	root->RightChild->RightChild = createNode(7);

	printf("Preorder traversal: ");
	preorderTraversal(root);
	printf("\n");

	printf("Inorder traversal: ");
	inorderTraversal(root);
	printf("\n");

	printf("Postorder traversal: ");
	postorderTraversal(root);
	printf("\n");

	printf("Level order traversal: ");
	LevelOrder(root);
	printf("\n");

	// 释放内存
	// ... (需要实现释放内存的函数)

	return 0;
}

运行结果如下：