HIT-SC-Lab1 BFS算法求图(边权为1)中两顶点之间最短距离(JAVA)

一、前言

1、广度优先搜索算法（Breadth First Search）

广度优先搜索算法(BFS)是最简便的连通图的搜索算法之一，这一算法也是很多重要的图的算法的原型。

BFS 是一种图形遍历方法，从源节点开始，通过图形逐层分析与源节点相邻的节点。然后，在 BFS 遍历中，依次移动到下一级相邻节点。

BFS在广度方向上遍历图形：

① 首先，水平移动并访问当前层的所有节点。

② 继续访问下一层，直至遍历完整个连通图。

广度优先搜索使用队列(Queue)数据结构来存储节点并将其标记为“已访问”，直到它标记了所有相邻顶点。队列按先进先出(FIFO)原则运行，因此将按照节点中插入邻居的顺序查看节点的邻居，从首先插入的节点开始。

2、广度优先搜索算法(BFS)的优点

 ① BFS 算法具有简单可靠的体系结构。

 ② BFS 算法有助于评估图形中的节点，并确定遍历节点的最短路径。

 ③ BFS 算法可以在尽可能少的迭代次数内遍历图形。

 ④ BFS算法中的迭代是平滑的，并且此方法无法陷入无限循环。

二、BFS求图中两顶点之间距离的基本思想

1、基本思想

① 首先访问起始节点，距离为0。

② 继续访问下一层节点。当访问到该层最后一个节点时，距离加1。

③ 重复步骤②，直至访问到终点节点，结果为距离加1。若搜索结束仍未访问到终点节点，则距离为-1，表示两节点不连通。

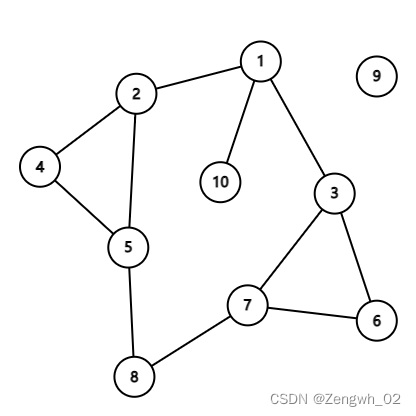
 2、示例

①首先访问第一层节点，即起点1，距离初始化为0

 ②然后访问第二层节点。若终点为节点2或节点10或节点3，则返回距离加1，即为1。否则，访问完第二层最后一个节点3时，距离加1，即为1，然后继续访问第三层。

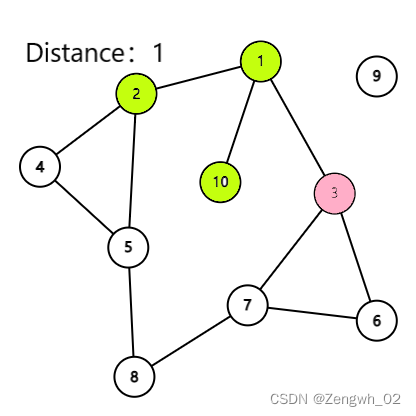
③ 然后访问第三层节点。若终点为节点4或节点5或节点7或节点6，则返回距离加1，即为2。否则，访问完第三层最后一个节点6时，距离加1，即为2，然后继续访问第四层。

 ④ 然后访问第四层节点。若终点为节点8，则返回距离加1，即为3。否则，若终点为节点9，那么在访问完节点8之后队列为空，未访问到节点9，则返回-1。

 三、实现代码如下

1、构造Person类

public class Person {
    private String name;
    private boolean flag = false;//flag代表BFS中是否访问过
    
    //带参构造
    public Person(String name) {
        this.name = name;
    }

    //返回Person的名字
    public String getName() {
        return name;
    }

    //更改Person的名字
    public void setName(String name) {
        this.name = name;
    }

    //返回flag值
    public boolean getFlag() {
        return flag;
    }

    //更改flag的值
    public void setFlag(boolean flag) {
        this.flag = flag;
    }
}

2、构建图(graph)

用哈希表(HashMap)构造图(graph)，其中键值(Key)对应顶点Person，数值(Value)对应邻居List<Person>。

Map<Person, List<Person>> graph = new HashMap<>();

3、实现getDistance()方法

public int getDistance(Person person1, Person person2) {
        //当是同一个人时
        if (person1 == person2) {
            return 0;
        }
        //将图中顶点Person.flag初始化
        Set<Person> set = graph.keySet();
        Person[] ps = new Person[set.size()];
        set.toArray(ps);
        for (int i = 0; i < ps.length; i++) {
            ps[i].setFlag(false);
        }
        //构建队列，并将第一个人person1加入队列
        Queue<Person> queue = new LinkedList<>();
        queue.add(person1);
        person1.setFlag(true);
        int result = 0;//result记录距离
        Person last = person1;//记录遍历的每一行最后一个顶点
        Person latest = person1;//记录此时此刻遍历的最后一个顶点
        //循环直至队列非空，即图中顶点尚未遍历完全
        while (!queue.isEmpty()) {
            List<Person> edge = graph.get(queue.peek());//出队列顶点的相邻顶点集
            Person out = queue.poll();
            //遍历该顶点集
            for (int i = 0; i < edge.size(); i++) {
                //当遍历到目标顶点person2时，直接返回
                if (edge.get(i) == person2) {
                    return result + 1;
                }
                //当该顶点未遍历过，加入队列并更新latest顶点
                if (!edge.get(i).getFlag()) {
                    queue.add(edge.get(i));
                    latest = edge.get(i);
                    edge.get(i).setFlag(true);
                }
            }
            //当遍历完该层最后一个顶点时，距离加1，并更新该层最后一个顶点
            if (out == last) {
                result++;
                last = latest;
            }
        }
        //当遍历完person1的所在连通集仍未找到person2
        return -1;
    }