C++位图

最新推荐文章于 2025-03-14 20:12:48 发布

Hero 2021

最新推荐文章于 2025-03-14 20:12:48 发布

阅读量719

点赞数

分类专栏： C++ 文章标签： c++ 开发语言

本文链接：https://blog.youkuaiyun.com/weixin_57675461/article/details/130733145

版权

C++ 专栏收录该内容

33 篇文章

订阅专栏

文章目录

一、面试题

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

遍历，时间复杂度O(N)
排序(O(NlogN))，利用二分查找: logN （2³⁰ =30亿，大概找32次即可找到）

1G空间=1024* 1024 * 1024Byte=10亿Byte
40亿个整数=40亿个int = 160亿Byte=16G内存
这在内存中一次能够放的下吗？
答案显而易见
如果使用哈希表或者红黑树来存储这些数字，那么附带的消耗也是巨大的

位图解决

位图是一种直接定址法的哈希，因此效率很高，用O(1)就可以探测到对应位是0还是1，效率非常高，因此可以快速判断
数据是否在给定的整形数据中，结果是在(1)或者不在(0)，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在。

40亿个整数=我们要开40亿个比特位
40亿bit = 40亿b / 8 /10亿 = 0.5G=500M 空间
可想而知，这是多么的省空间

但是我们这里要开42亿个比特位！这是为啥呢？
因为我们采用的直接定址法，要是我开40亿个位置，注意unsigned int范围：0-42亿，那么万一有个数是MAX，岂不是没有办法映射了。

咱们C++开空间是怎么开的？
是不是要先确定一个类型，才能开，那么最小的类型就是char 了
我们可以控制这个char，来实现控制bit位

std::vector<char> _bits;

二、位图核心函数的实现

set 设置指定位或所有位
reset 清空指定位或所有位
test 获取指定位的状态

简单的使用：

#include <iostream>
#include <bitset>

using namespace std;

int main()
{
	bitset<8> bs;
	cout << bs << endl; // 00000000
	bs.set(1); // 设置第1位
	bs.set(7); // 设置第7位
	cout << bs << endl; // 10000010

	cout << bs.test(1) << endl; // 看看第1位是啥  1 
	cout<< bs.test(2) << endl;  // 看看第2位是啥  0
	cout << bs.test(7) << endl; // 看看第7位是啥  1
	cout << bs << endl; // 10000010

	bs.reset(1); // 清空第1位
	cout << bs << endl; // 10000000
	return 0;
}

在这里插入图片描述

如何把第j位置为1？其他位都是0

在这里插入图片描述

在这里插入图片描述
测试：

所以：
第一个char 0010 0000
第二个char 0000 0100
第三个char 0001 0000

如何把第j位置为0？其他位都不变

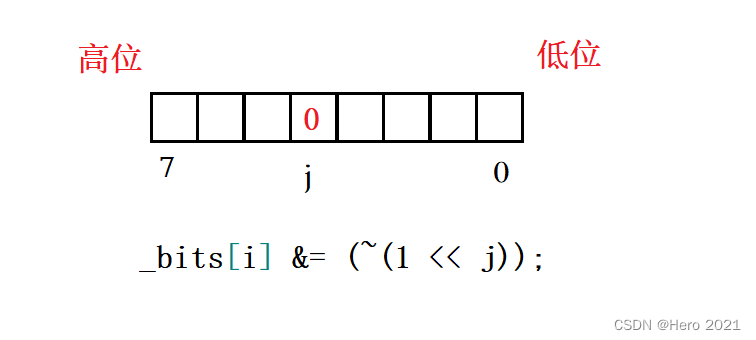
在这里插入图片描述

在这里插入图片描述
最后只剩下2了

如何检测第j位为0还是1？

在这里插入图片描述

模拟实现

namespace sjj
{
	template<size_t N>
	class bit_set
	{
	public:
		bit_set()
		{
			_bits.resize(N / 8 + 1);// 比如我要开10个比特位 N=10 ， 10/8=1 那么很明显不够，那么我们就多加1，现在相当于我们有2个char，16比特位
		}

		//
		///  三个核心函数接口
		//
		void set(size_t x)
		{
			size_t i = x / 8; // 确定它在哪个char上
			size_t j = x % 8; // 确定它在该char的具体第几个位置

			_bits[i] |= (1 << j);
		}
		void reset(size_t x)
		{
			size_t i = x / 8; 
			size_t j = x % 8;

			_bits[i] &= (~(1 << j));
		}
		bool test(size_t x)
		{
			size_t i = x / 8;
			size_t j = x % 8;

			return _bits[i] & (1 << j);
		}
	private:
		std::vector<char> _bits;
	
	};
	void test_bit_set()
	{
		bit_set<100> bs;
		bs.set(5);
		bs.set(10);
		bs.set(20);
		bs.set(1);

		cout << bs.test(5) << endl;
		cout << bs.test(20) << endl;
		bs.reset(20);
		bs.reset(10);
		bs.reset(5);

		cout << bs.test(5) << endl;
		cout << bs.test(20) << endl;
	}
}

解决开头的面试题

首先文件读取，将这40亿个数分批次读取到内存(fstream)，然后设置到我们的位图结构中

这样开空间：

bit_set<0xffffffff> bs;
bit_set<-1> bs; // -1存的是补码，原码是全1，就是最大值

三、位图的应用

1、给定100亿个整数，设计算法找到只出现一次的整数？

位图的变形题
100亿个整数=100亿个int=40G内存
注意题目是找只出现一次的数字，那么难免会有的数字出现多次，所以的数字共有42亿个

所以我们要分为三种状态：

出现0次
出现1次
出现2次及以上

一个位可以表示两个(0 1)状态，三种状态我们需要2个比特位，意思就是说，我们需要开两个位图，这两个位图的对应位置分别表示该位置整数的第一个位和第二个位。
三种状态定义为：00 01 10，当我们读取到重复的整数时，就可以让其对应的两个位按照00→01→10的顺序进行递增变化，最后状态是01的整数就是只出现一次的整数。
在这里插入图片描述

template <size_t N>
class TwoBitSet
{
public:
	
	void Set(size_t x)
	{
		if (!bs1.test(x) && !bs2.test(x)) // 00 ->01
		{
			bs2.set(x);
		}
		else if (!bs1.test(x) && bs2.test(x)) // 01 ->11
		{
			bs1.set(x);
			bs2.reset(x);
		}
		// 表示x已经出现过2次以上的了，不用处理了
	}

	void PrintfOnceNum()
	{
		for (size_t i = 0; i < N; i++)
		{
			if (!bs1.test(i) && bs2.test(i))
			{
				cout << i << endl;
			}
		}
	}
private:
	bitset<N> bs1;
	bitset<N> bs2;
};

void testTwoBitSet()
{
	int a[] = { 1,1,2,2,99,55,55 };
	TwoBitSet<100> tbs;
	for (auto e: a)
	{
		tbs.Set(e);
	}
	tbs.PrintfOnceNum();
}