插入，选择和冒泡排序原理

插入排序

//插入排序的基本思想：
//1.外层循环控制每趟，一般是数组元素长度减一次，因为最后一次不需要在进行排序
//2.内层循环控制每趟的次数，每次让当前索引元素与下一个索引位置元素进行比较，将将大的放在后面
//并且每趟的次数是依次减少的
//例如,对于数组{13,24,1,25,67,54,37,28,81,2}
//第一趟{13} 24，1，25，67，54，37，28，81，2
//第二趟{13，24} 1，25，57，54，37，28，81，2
//第三趟{1，13，24} 25，57，54，37，28，81，2
//第四趟{1，13，24，25} 57，54，37，28，81，2
//第五趟{1，13，24，25，57} 54，37，28，81，2
//第五趟{1，13，24，25，54，57} 37，28，81，2
//第六趟{1，13，24，25，37，54，57} 28，81，2
//第七趟{1，13，24，25，28，37，54，57} 81，2
//第八趟{1，13，24，25，28，37，54，57，81} 2
//第九趟{1，2，13，24，25，28，37，54，57，81}
//数组长度为10，需要继续进行9趟排序，外层排序次数为(数组.length - 1)
//平均时间复杂度为O(n^2),最坏时间复杂度为O(n^2)
//对于第一趟排序{13,24,1,25,67,54,37,28,81,2}
//此时i为0指向13，j为0指向13，取24开始与13比较 13 < 24,不用交换24现在在13后
//且此时13，24保持在整个数组中保持局部有序
//第二趟j为0指向13，j+1为2指向1， 1 < 13,交换，然后j为1指向24，j+1 为2指向13，13 < 24,交换
//依次进行每趟，重复上述步骤
//第一轮一共比较了1次交换1次，比较次数一定但交换次数不定

//注：上图的名字写的是MaoPao但这部分是插入排序，（小小失误）冒泡排序随后会补充

选择排序

//选择排序的基本思想：
//选择排序的基本思想是每次挑一个最小的放到数组后面的位置
//例如对于数组{13,24,1,25,67,54,37,28,81,2}
//第一轮{1} 24,2,25,67,54,37,28,82,13
//第二轮{1,2} 13,25,67,54,37,28,82,24
//第三轮{1，2，13} 24，25，67，54，37，28，81
//第三轮{1，2，13，24} 25，67，54，37，28，81
//第四轮{1，2，13，24，25} 67，54，37，28，81
//第五轮{1，2，13，24，25，28} 67，54，37，81
//第六轮{1，2，13，24，25，28，37} 67，54，81
//第七轮{1，2，13，24，25，28，37，54} 67，81
//第八轮{1，2，13，24，25，28，37，54，67} 81
//第九轮{1，2，13，24，25，28，37，54，67，81}
//显然第几轮比较是非必要的，当进行完第八轮比较时，数组已经有序
//数组含有十个元素，比较八次，比较次数为（数组.length - 2）
//平均时间复杂度O(n^2) 最坏时间复杂度O(n^2)
//对于数组{13,24,1,25,67,54,37,28,81,2}
//第一轮：{1} 24,2,25,67,54,37,28,82,13
//分析:此时i为0指向13，j指向9指向2,2 < 13,因此交换2和13的位置
//接着i为0指向2，j为8指向82，82 !< 2，显然不用交换位置
//继续i为0指向2，j为7指向28，28 !< 2,显然不用交换位置
//...然后i不变，j一直--，并且一直比较
//直到i为0指向2，j为2指向1，此时 1 < 2,交换位置
//然后i为零指向1，j为1指向24，此时 1 < 24,不用交换位置
//然后j--为0，j !< i,第一轮循环结束，开始第二轮循环，重复上述步骤
//第一轮比较了9次，交换了两次，比较的次数是相对固定的，只要给定数组长度就行，与原始数组的内部序列无关
//而交换的次数不定，与原始数组内部序列有关，但是小于比较次数

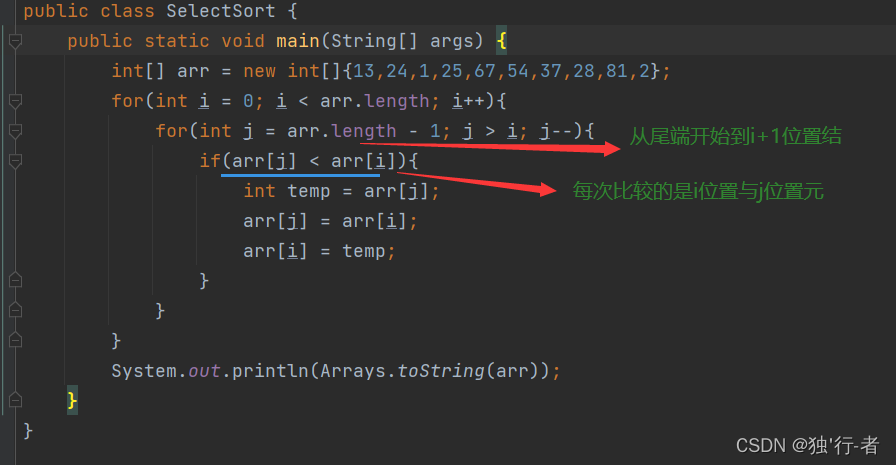
选择与插入排序的区别

选择排序是没次选一个最大或者最小的元素，放到部分有序序列中，选的时候需要比较，但是放入的时候并不需要比较（因为每次都是挑一个最大/最小的放在末尾，那么下一次的肯定比上一次末尾的元素还要大/小）。

插入排序是每次拿一个元素放在有序序列的合适位置，拿的时候不用比较，直接拿到索引位置元素，放入部分有序序列的时候，需要从末尾开始逐个比较，放入合适位置。

概括起来就是一句话：选择排序，先比后放，插入排序，先拿后比。

冒泡排序

//冒泡排序的基本思想：
//以升序为例，每次从数组首部向数组尾部处理，用一个辅助变量来指向第一个元素
//然后依次向后和下一个临近元素进行比较
//如果待比较元素比前一个元素大的话，将这个指针指向较大元素
//然后依次处理到最后，那么这个新出的元素就是可以添加到局部有序部分的首部，重复上述步骤即可
//举例如下：
//对于数组：{13,24,1,25,67,54,37,28,81,2}
//第一趟：{13，1，24，25，54，37，28，67，2} 81
//第二趟：{1，13，24，25，37，28，54，2} 67，81
//第三趟：{1，13，24，25，28，37，2} 54，67，81
//第四趟：{1，13，24，25，28，2} 37，54，67，81
//第五趟：{1，13，24，25，2} 28，37，54，67，81
//第六趟：{1，13，24，2} 25，28，37，54，67，81
//第七趟：{1，13，2} 24，25，28，37，54，67，81
//第八趟：{1，2} 13，24，25，28，37，54，67，81
//第九趟;{1 } 2，13，24，25，28，37，54，67，81
//第十趟未排序部分只剩一个元素，肯定是最小值，不用再比较，10个元素比较9趟，比较(数组.length-1)趟
//对于第一趟分析：{13,24,1,25,67,54,37,28,81,2} arrays[j]为最大值
//i=0，j=i=0指向13，13与24比较 13<24，24与1比较24 !< 1因而交换24和1的位置，继续向后24与25比较
//24 < 25不较换，25 < 67交换 67 !< 28交换...
//依次执行上述操作，每次最大值都会“浮”到最后，这也是冒泡排序的由来

 

目录

插入排序

 选择排序

 选择与插入排序的区别

冒泡排序

---