【PyTorch深度学习实践】01_线性模型

线性模型

1.深度学习的数据

训练集、测试集、验证集

2.线性回归

已知如下数据集（dataset），目的是解决预测的问题：

因为数据集并不复杂，可以考虑构建线性回归模型进行预测，为了简化，可以构造如下模型：

其中，不同的w会产生不同的直线，可以通过损失函数来计算误差，选择效果最好的一个。
损失函数有许多种，这里展示一种计算方式——MSE（平均平方误差）

图中上方的公式是针对单个样本的误差计算，下方的公式是针对整个训练集（training set）的误差计算。

3.实现代码

import numpy as np               # 导入必须的包
import matplotlib.pyplot as plt

# 1.建立线性模型
x_data = [1.0, 2.0, 3.0]  # 数据集整理
y_data = [2.0, 4.0, 6.0]

def forward(x):      # 定义线性模型
    return x * w

def loss(x,y):        # 定义损失函数
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)

w_list = []         # 权重w的列表
mse_list = []       # 每个w的mse值

for w in np.arange(0.0, 4.1, 0.1):  # 从0.0开始，步长0.1，一直到4.0
    print("w=" , w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)      # 仅为了输出，没什么特别意思
        loss_val = loss(x_val, y_val)
        l_sum += loss_val
        print('\t',x_val,y_val,y_pred_val,loss_val)
    print("MSE=",l_sum / 3)
    w_list.append(w)
    mse_list.append(l_sum / 3)

# 2.画图
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

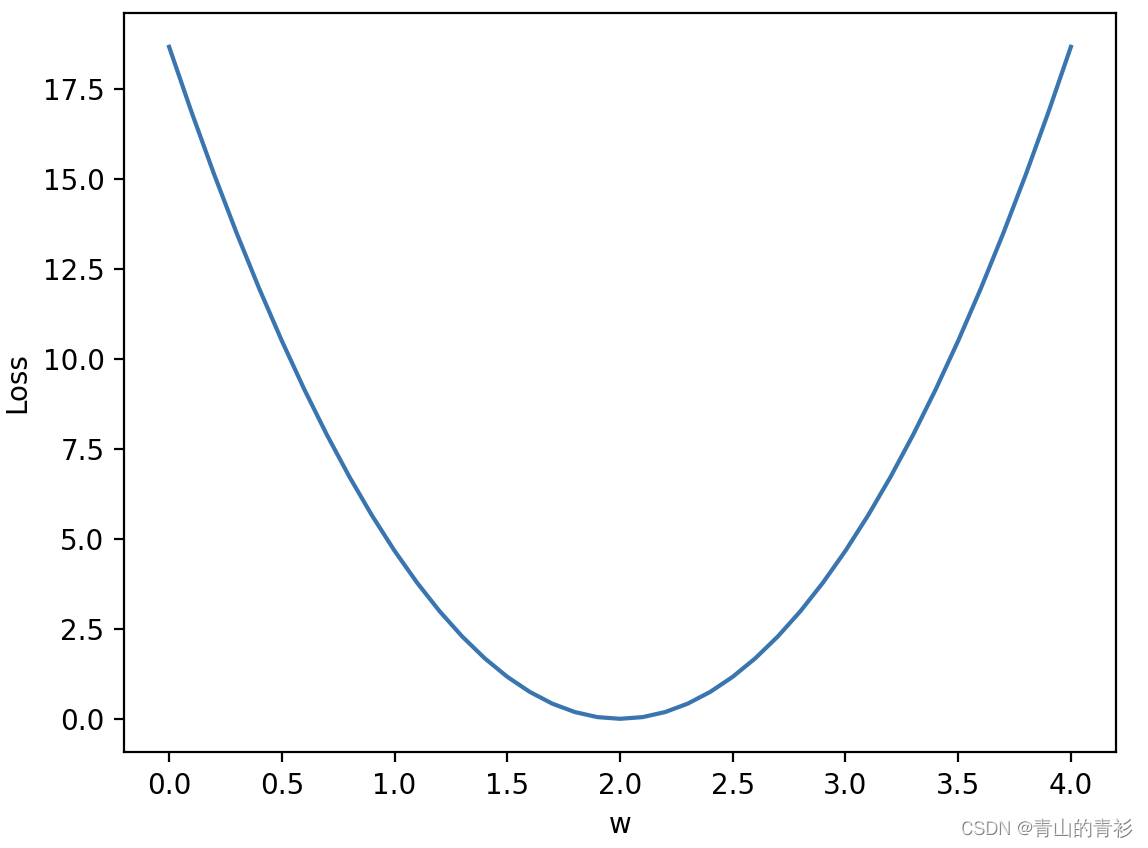
输出图片如下：