CF系列题解
Codeforces Round #788 (Div. 2)
题目
A. Prof. Slim
原题链接
题意
给定一个序列,每次操作可以交换一个正数和一个负数的符号,能否进行若干次操作后使得序列不降。
题解
思路
把所有的负号移到前面即可。(刚开始都错题以为是交换正负数然后写了个大模拟样例没过,有点恶心)
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve()
{
int n;
cin >> n;
vector<int> a(n);
int cnt = 0;
for (int i = 0; i < n; i ++ ) {
cin >> a[i];
if (a[i] < 0) cnt ++ ;
}
for (int i = 0; i < cnt; i ++ ) {
if (a[i] > 0) a[i] = -a[i];
}
for (int i = cnt; i < n; i ++ ) {
if (a[i] < 0) a[i] = -a[i];
}
if (is_sorted(a.begin(), a.end())) cout << "YES\n";
else cout << "NO\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T -- ) {
solve();
}
return 0;
}
B. Dorms War
原题链接
题意
给定一个字符串和一个字符集合,每次可以选择当前字符串中所有的在集合中出现过的字符,并删除其前方的字符,问需要操作多少次后不能再继续操作。
题解
思路
首先我们不考虑边界,假设 c i c_i ci 为前一个出现在集合中的字符, c j c_j cj 为后一个,且 c i + 1 c i + 2 . . . c j − 1 c_{i+1}c_{i+2}...c_{j-1} ci+1ci+2...cj−1 均不包含在集合内,因此需要的操作数为 j − i j-i j−i,即删除 c i c_{i} ci 到 c j − 1 c_{j-1} cj−1 需要进行 j − i j-i j−i 次操作,双指针即可。
对于出现在最左边的字符 c i c_i ci,倘若其在字符集合中,那么需要 i − 1 i-1 i−1 步可以把其前缀全部删除。
出现在最右边的字符,显然永远无法删除其及其后缀,跳过即可。
将上面的情况取最大即可。
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
void solve()
{
int n;
cin >> n;
string s;
cin >> s;
int k;
cin >> k;
set<char> S;
while (k -- ) {
char c;
cin >> c;
S.insert(c);
}
int ans = 0;
for (int i = 0; i < n; i ++ ) { // 处理最左边
if (S.count(s[i])) {
ans = i;
break;
}
}
for (int i = 0; i < n; i ++ ) {
if (S.count(s[i])) { // 经典双指针
int len = 1;
int j = i + 1;
while (j < n && !S.count(s[j])) {
j ++ ;
len ++ ;
}
if (j == n) break; // 倘若其右边没有字符,break即可
i = j - 1;
ans = max(ans, len);
}
}
cout << ans << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T -- ) {
solve();
}
return 0;
}
C. Where is the Pizza?
原题链接
题意
给定两个排列
a
a
a 和
b
b
b,以及一个序列
c
c
c,可以对
c
c
c 中为
0
0
0 的部分进行如下操作:
若
c
i
=
0
c_i=0
ci=0,可以令
c
i
=
a
i
c_i=a_i
ci=ai 或
c
i
=
b
i
c_i=b_i
ci=bi。
若使得最终得到的 c c c 序列也为一个排列,有多少种可能。
保证存在一组解。
题解
思路
首先确定一点,假设当前位置 a i ≠ b i a_i≠b_i ai=bi,倘若 c i = a i c_i=a_i ci=ai 时,我们找到 a j = b i a_j=b_i aj=bi,此时 c j c_j cj 只能等于 a j a_j aj,倘若 a j ≠ b j a_j≠b_j aj=bj,我们就可以重复上述步骤直到 b = a i b=a_i b=ai,而这些记录的位置都可以算在一起,因为你选择其中一个的话,其他所有的选择都已经确定了,因此每个这样的循环都对应 2 2 2 个方案,即每存在一个这样的循环答案乘 2 2 2。
根据题目给定的条件以及上述结论可以确定 c c c 中的一些位置,我们将其标记,这些位置是永远不会动的。
然后对无法确定的位置枚举找出一共有多少个上述循环即可。
(好像可以用并查集,先贴一个比赛时的shit代码,写了一百行的大模拟呜呜呜)
代码
#include <bits/stdc++.h>
using namespace std;
constexpr int P = 1e9+7;
using i64 = long long;
// assume -P <= x < 2P
int norm(int x) {
if (x < 0) {
x += P;
}
if (x >= P) {
x -= P;
}
return x;
}
template<class T>
T power(T a, int b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x % P)) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(P - x));
}
Z inv() const {
assert(x != 0);
return power(*this, P - 2);
}
Z &operator*=(const Z &rhs) {
x = i64(x) * rhs.x % P;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend istream& operator>> (istream& is, Z& z) {
is >> z.x;
z.x = (z.x % P + P) % P;
return is;
}
friend ostream& operator<< (ostream& out, const Z& z) {
out << z.x;
return out;
}
};
void solve()
{
int n;
cin >> n;
vector<int> a(n), b(n), c(n), ida(n + 1), idb(n + 1);
vector<bool> st(n), nst(n + 1);
for (int i = 0; i < n; i ++ ) {
cin >> a[i];
ida[a[i]] = i;
}
for (int i = 0; i < n; i ++ ) {
cin >> b[i];
idb[b[i]] = i;
}
for (int i = 0; i < n; i ++ ) {
cin >> c[i];
if (c[i]) {
nst[c[i]] = true;
st[i] = true;
}
}
vector<int> sst(n);
// 预处理确定的部分
for (int i = 0; i < n; i ++ ) {
if (c[i] && !sst[i]) {
sst[i] = true;
if (a[i] == b[i]) continue;
if (c[i] == a[i]) {
int t = a[i];
int d = t;
for (int j = 0; ; j ++ ) {
st[ida[d]] = true;
sst[ida[d]] = true;
c[ida[d]] = d;
nst[d] = true;
d = b[ida[d]];
if (d == t) break;
}
} else {
int t = b[i];
int d = t;
for (int j = 0; ; j ++ ) {
st[idb[d]] = true;
sst[idb[d]] = true;
c[idb[d]] = d;
nst[d] = true;
d = a[idb[d]];
if (d == t) break;
}
}
}
}
// 未确定的部分
for (int i = 0; i < n; i ++ ) {
if (!st[i]) {
if (nst[a[i]]) {
c[i] = b[i];
nst[c[i]] = true;
st[i] = true;
}
if (nst[b[i]]) {
c[i] = a[i];
nst[c[i]] = true;
st[i] = true;
}
if (a[i] == b[i]) {
c[i] = a[i];
nst[c[i]] = true;
st[i] = true;
}
}
}
// for (int i = 0; i < n; i ++ ) cout << st[i] << " ";
// cout << "\n";
Z ans = 1;
for (int i = 0; i < n; i ++ ) {
if (!st[i]) {
ans *= 2;
int t = a[i];
int d = t;
for (int j = 1; ; j ++ ) {
st[ida[d]] = true;
d = b[ida[d]];
if (d == a[i]) break;
}
}
}
cout << ans << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T -- ) {
solve();
}
return 0;
}
D. Very Suspicious
原题链接
题意
给定一个无限六边形网格,每次添加一条平行于六边形边的线,可以分割出若干个三角形。
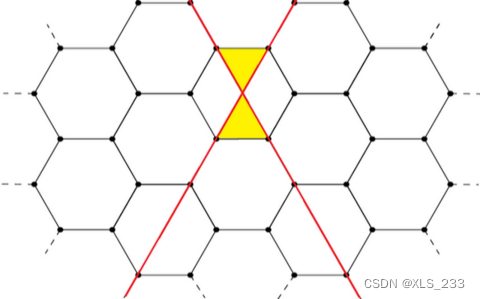
给定最终得到的三角形数目,问至少需要多少根线才能分割出这些数目的三角形。
题解
思路
首先明确一点,倘若两条线相交,会多出 2 2 2 个三角形。倘若我们新添加一条线与 c n t cnt cnt 条线相交,那么会多出 2 × c n t 2×cnt 2×cnt 个三角形。
接下来的任务就变为了计算添加一条线能与最多多少条线相交。
我们将线分为三类:

其中蓝色为
a
a
a 类,红色为
b
b
b 类,黄色为
c
c
c 类。
我们每次添加肯定是在数量最少的类别中添加,只有这样才能保证其与另外两类相交的最多。由于我们每次都在最少的类别中添加,因此三种线的数目之差不可能大于 1 1 1,因此假设我们当前要添加第 i i i 条线,那么其与之前 i − 1 i-1 i−1 条线相交最多应该为 i − 1 − ( i − 1 ) / 3 i-1-(i-1)/3 i−1−(i−1)/3,其中除法为下取整。
预处理出来直接二分查找即可,推荐使用 lower_bound。
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 40000;
int num[N], len;
void init()
{
for (int i = 2; i < N; i ++ ) {
int cnt = i - 1 - (i - 1) / 3;
num[i] = num[i - 1] + cnt * 2;
if (num[i] > (int)1e9) {
len = i;
break;
}
}
}
void solve()
{
int n;
cin >> n;
cout << lower_bound(num, num + len, n) - num << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
int T;
cin >> T;
while (T -- ) {
solve();
}
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








