本文适合明白kmp原理,但还有疑惑的朋友看,故而KMP原理不作讲解。kmp原理请自行百度。
kmp的常见疑惑:
- 为什么移动模式串的过程中不会有遗漏?
- 为什么要用最大相同前后缀?
- next数组到底是什么,怎么求?
- 理解原理,代码看不懂,不会写,怎么办?
1. 为什么移动模式串时不会有遗漏?
--------为完全匹配的任意字符
AB为最大相同前后缀,如果不了解什么是最大相同前后缀,请下滑先看3.关于前后缀的介绍
首先我们在下标9处失配

那么按照kmp 算法我们会移动子串至最大相同前后缀AB处

那么假设现在,我们有遗漏,在下图处恰好匹配

那么最大的相同前后缀应该是,红色框内的

但是前面已经说过了,最大相同前后缀是 AB,那么

这种情况与最大相同前后缀是 AB相冲突,所以不可能出现。
如果在移动过程中,出现了恰好完全匹配的情况,那么只能说明,我们找的最大相同前后缀是错的,并不是最大的。
2.为什么要用最大相同前后缀?
其实看到此处,且认真看懂了1.的话,应该已经明白了,使用最大相同前后缀,就是为了,避免移动模式串的过程中出现遗漏的情况。
3.next数组到底是什么,怎么求?
next数组只是一个工具,根据不同的定义,会得到不同的值。
常见的 是以-1 ,0 开头,或者以0 ,1开头的,考研用的也是这两种,但是我没有了解过这两种,而接下来我要介绍的是一种完全不同的next数组的定义。
next数组的值是代表着字符串的前缀与后缀相同的最大长度,即最大相同前后缀的长度,可能这句话现在让你无法理解,请耐心看下去。
介绍next数组就不可避免需要理清楚前后缀的脉络。
1.何为前后缀
那么假定模式串为“01010”
前缀不可包含最后一个字符,后缀不可包含第一个字符。
“0” 这个串既无前缀也无后缀,因为0既是第一个也是最后一个字符。 故next[0]=0
“01” 前缀:0 后缀:1 0和1没有相同处。故而next[1]=0
“010” 前缀:01 后缀:10 01和10,0相同,0为最大相同前后缀,故next[2]=1
“0101” 前缀:010 后缀:101 01和01相同,01为最大相同前后缀故next[3]=2
“01010” 前缀:0101 后缀:1010 010和010相同,010为最大相同前后缀故next[4]=3
2.那么如何求取next数组呢?
讲解未动,代码先行,看不懂没关系,继续往下看。
void GetNext(const string &s ,int* const next)
{
next[0] = 0;
int len = s.length();
for (int i = 1, j = 0;i < len;i++)
{
while (j > 0 && s[i] != s[j])
{
j = next[j - 1];
}
if (s[i] == s[j])
{
j++;
}
next[i] = j;
}
}代码大家应该是看不懂的,耐心看了讲解回头看代码就好。

假如黄色框内和绿色框内的第一个待匹配的字符串相同,由于黑色框内是长度j的最大相同前后缀,那么 next[ 黄色框第一个字符处 ] =j+1,假如黄色框内和绿色框内的第二个待匹配的字符串相同
,那么next[ 黄色框第二个字符处 ] =j+2;

上述是关于相等时的情况,那么假如s[i]!=s[j]呢?
重新举一个例子:
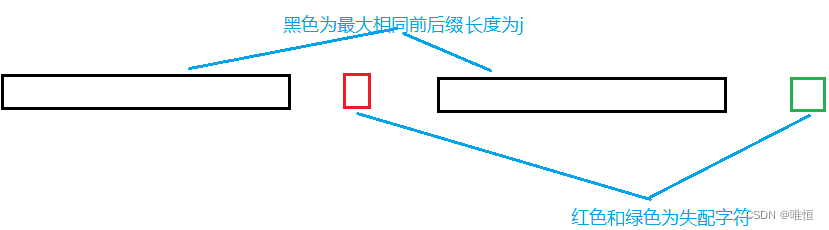
按照代码

当不相等时:j=next[j-1] ,即如下图:

好了,到此为止,大家应该已经明白了next数组的求法。
4.理解原理,代码看不懂,不会写,怎么办?
讲解未动,代码先行,看不懂没关系,继续往下看。:
/****************************************************
> File Name: KMP
> Author: 唯恒
> Mail: 2279811789@qq.com
> Created Time: 2022年10月22日
*******************************************************/
#include <iostream>
using namespace std;
void GetNext(const string &s ,int* const next)
{
next[0] = 0;
int len = s.length();
for (int i = 1, j = 0;i < len;i++)
{
while (j > 0 && s[i] != s[j])
{
j = next[j - 1];
}
if (s[i] == s[j])
{
j++;
}
next[i] = j;
}
}
int Kmp(const string &s,const string &t)
{
int* const next = new int[t.length()];
GetNext(t, next);
for (int i = 1, j = 0;i < s.length();i++)
{
while (j > 0 && s[i] != t[j])
{
j = next[j - 1];
}
if (s[i] == t[j])
{
j++;
}
if (j == t.length())
{
return i - j + 1;
}
}
return -1;
}
int main()
{
string s = "ABCDDDABA";
string t0 = "ABA";
int i= Kmp(s, t0);
if ( i!=-1)
{
cout << Kmp(s, t0) << endl;
}
else
{
cout << "主串中无子串" << endl;
}
string t1 = "ABc";
i = Kmp(s, t1);
if ( i != -1)
{
cout << Kmp(s, t1) << endl;
}
else
{
cout << "主串中无子串" << endl;
}
return 0;
}
//111,0,111,1首先i是主串的下标,kmp主串指针不会后移,故而在在for里i++,每一轮都要增加。

其次如果s[i]和t[j]相等那么移动模式串指针,让模式串下一个字符和主串下一个字符比较。
当j==模式串长度时,说明模式串已经比较到末尾了。返回i-j+1,因为返回的是模式串在主串中第一次出现的位置,所以需要减去模式串的长度,+1是因为人们习惯于从1开始计数,如果像数组一样从0开始,不+1也可以。
接下来:
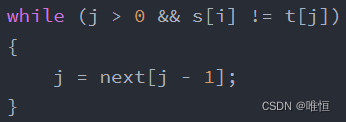
当s[i]!=t[j]时让j=next[j-1],即j=当前最大相同最大前后缀的长度。
举个例子吧

当0和1失配,那么0这个next[2]的最大相同前后缀为0,将j=0,下一次就差t[0]开始比较

假如一直找不到相等的,那么一直循环,当t[0]时还是!=的话,那么,因为![]()
退出循环,主串移动指针 ,让下一个指针和模式串的t[0]比较。
最后
![]()
当for结束还是没有找出的话,说明主串里找不到模式串,返回-1。
结语:
看不懂没关系,反复看就行,我也是看了很久才明白的,带入数据进程序手动运算,想想自己对kmp算法的原理是否彻底搞懂,再结合别的博客,b站上的视频理解。
姑妄言之,如是我闻,不喜勿喷。
大道唯恒,事注乃成;希翼列位斧正,愿同诸君共勉。

























 358
358

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








