zsjwl

分享-卷积神经网络基础

一、全连接神经网络

输入层->隐(藏)层->输出层，这个整称为全连接

神经元在隐藏层中

输入层常见的数据：(矩阵)图片。。。等

神经网络模型 y = model(x)

x是一个矩阵，可类比为图片的像素点

隐藏层有很多层隐藏层1、隐藏2

神经元的表达式 y = h（wx+b）

其中x、y分别是输入和输出，w是权重，b是偏置项，h是激活函数

二、激活函数

常见的激活函数 sigmoid

1.sigmoid函数常见的功能

二分类输出层：在二分类问题中，Sigmoid函数常用作输出层的激活函数，因为它能将输出解释为属于某一类的概率。

2.sigmoid函数的优点

输出结果介于0和1之间，非常适合用来表示概率，便于在二分类问题中作为输出层的激活函数

3.sigmoid函数的缺点

正向梯度消失和反向梯度爆炸的问题

三、卷积的简介

1.在通信领域中：

卷积是一种数学运算，它在信号处理、图像处理和深度学习中广泛应用。在一维卷积中，一个小的滤波器（或称为卷积核）在输入信号上滑动，计算滤波器与信号的局部区域的点积，生成一个新的输出信号，这有助于提取局部特征。

2.在卷积神经网络中

卷积神经网络（CNN）是一种深度学习架构，它利用卷积层来自动并有效地提取数据的层次结构特征。CNN在图像和视频识别、自然语言处理以及时间序列分析等领域表现出色。通过堆叠多个卷积层，CNN能够学习从简单到复杂的特征表示，从而在各种任务中实现高精度的预测和分类

3.卷积的参与对象

1.输入信号、输入图像或特征图（Feature Map）

可以简单理解为待处理的输入，可以是信号或者特征图

2.卷积核

一组可学习的权重，有助于识别和提取数据中的局部特征，如边缘、纹理、颜色等

四、不同的卷积

（设下列步长均为1，即stride=1）

1.一维卷积

1.*填充卷积 Valid卷积

常用的卷积

2.一维same卷积

same卷积基于卷积核的锚点，保持尺寸一致性，便于网络设计和后续层的尺寸匹配。

3.full卷积

输入特征图的边缘被扩展（通常填充零），以便卷积核可以覆盖到输入的边缘区域

卷积的计算规则

O代表输出，F代表卷积核

五、卷积在图像处理中的应用

对一张图片，我们需要通过卷积核来提取它的特征，如下动图

下图可以理解为一个9*9的图片经过3*3的卷积核valid卷积后的结果（下图只是模拟）

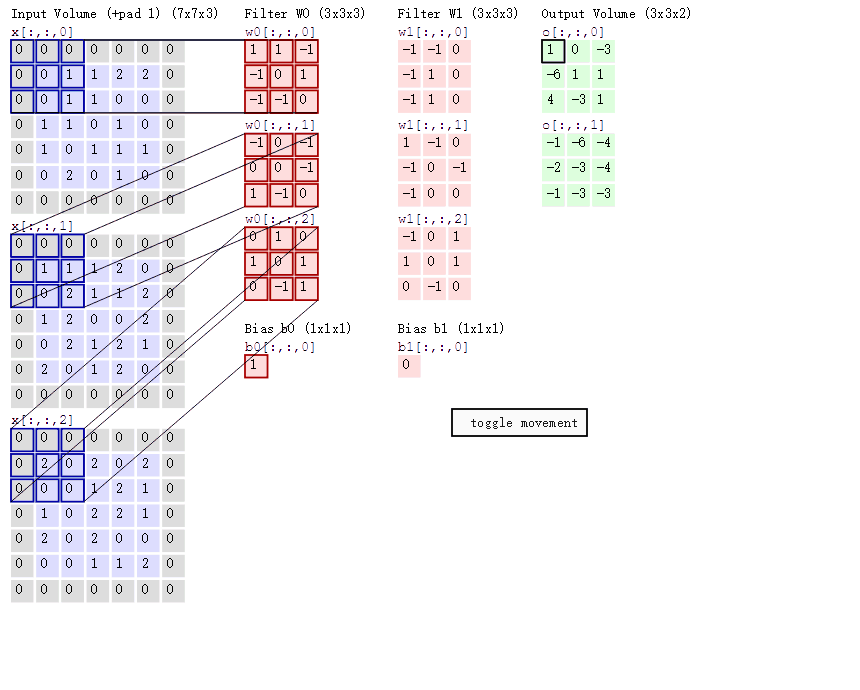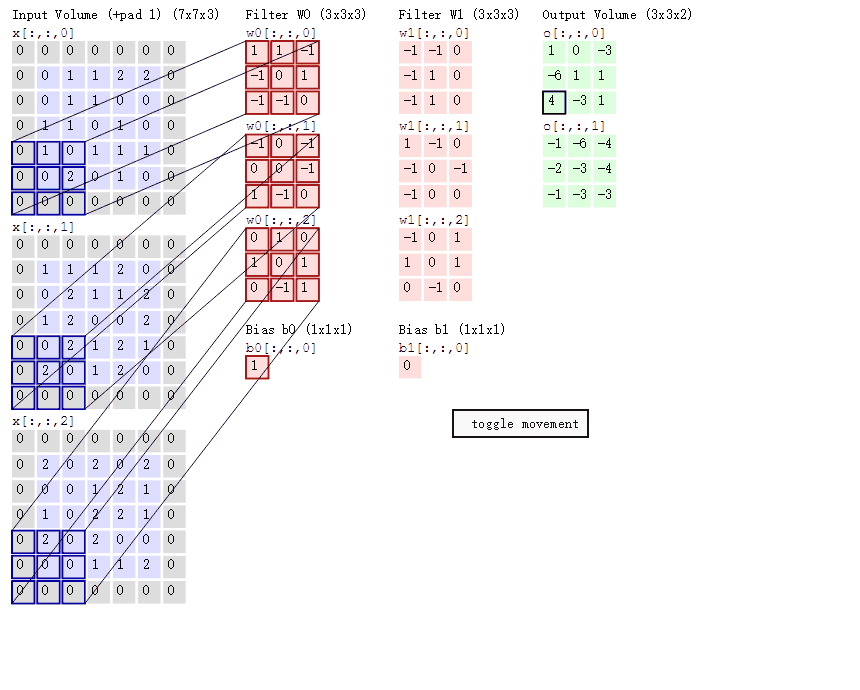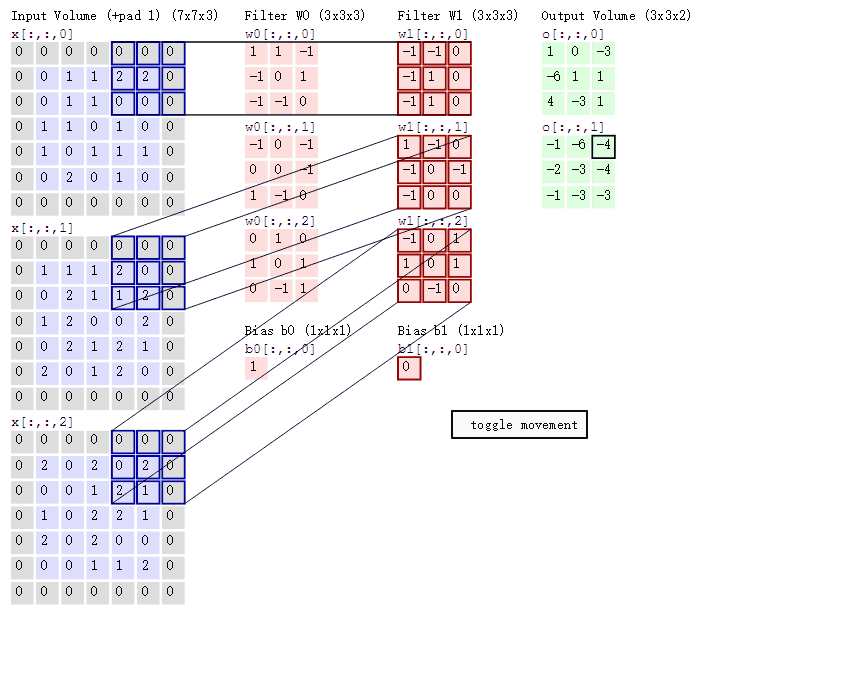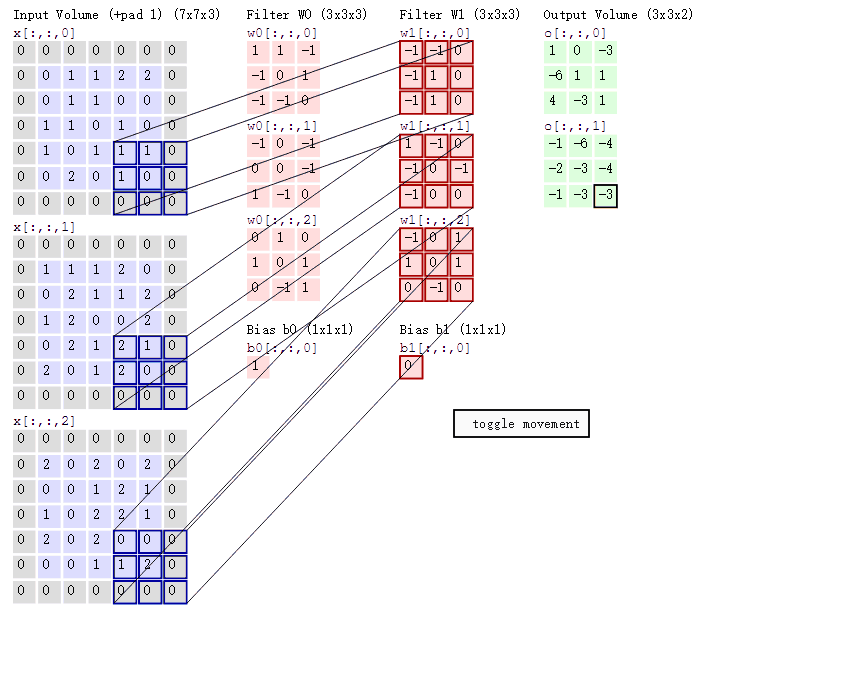
最终会生成一个7*7的结果，这个结果就可以是我们提取的一个特征

同样这个例子也可以用于对于同一图形翻转后的鉴定为同一图

六、池化

1. 池化-特征提取

最大池化

平均池化

七、整体结构

池化和卷积是卷积神经网络（CNN）中两种关键的操作，它们在特征提取和降维方面发挥着重要作用。以下是它们的主要区别：

卷积

• 定义：卷积是一种数学运算，通过滑动窗口（卷积核）在输入数据上滑动，并计算窗口内元素与对应卷积核元素的加权和，从而生成输出特征图

• 目的：用于特征提取，通过卷积核在输入数据上滑动计算加权和。

• 计算方式：卷积核在输入数据上滑动，计算每个位置上的加权和，并可能应用激活函数，以生成输出特征图

• 作用：通过滑动窗口(卷积核)与输入数据的局部区域进行卷积运算，从而提取出图像或信号的特定特征

池化

• 定义：池化是卷积神经网络中的一种下采样操作，通过定义一个空间邻域，并对该邻域内的特征进行统计处理（如取最大值、平均值等），从而生成新的特征图

• 目的：用于特征降维，通过聚合统计池化窗口内的元素来减少数据空间大小。

• 计算方式：通过定义一个空间邻域，并对该邻域内的特征进行统计处理（如取最大值、平均值等）。

• 作用：通过减少特征图的尺寸，降低了后续卷积层的计算量和参数数量，从而提高了计算效率