【Codeforces】CR984-Div3-d题-我爱1543

我爱 1543

每次测试时限：2 秒

每次测试内存限制：256 兆字节

输入：标准输入

输出：标准输出

一天早上，波利卡普一觉醒来，发现 $1543$ 是他一生中最喜欢的数字。

那天，波利卡普一睁开眼睛，首先看到的是一块面积为 $n$ 乘 $m$ 个单元的大墙毯； $n$ 和 $m$ 是偶数整数。每个单元格包含从 $0$ 到 $9$ 中的一个数字。

波利卡普好奇地想知道，如果按 顺时针方向穿过地毯的所有层 ，数字 $1543$ 会出现多少次。

大小为 $n\times m$ 的地毯的第一层被定义为长度为 $2\cdot (n+m-2)$ 、厚度为 $1$ 的封闭条带，环绕在其外部。之后的每一层都被定义为从原地毯上去除所有前几层后得到的地毯的第一层。

输入

输入的第一行包含一个整数 $t$ ( $1\le t\le 100$ ) - 测试用例的数量。下面几行描述测试用例。

每个测试用例的第一行包含一对数字 $n$ 和 $m$ （ $2\le n,m\le 10^3$ , $n,m$ - 偶数整数）。

之后是长度为 $m$ 的 $n$ 行，由 $0$ 至 $9$ 的数字组成，即地毯的描述。

保证所有测试用例中 $n\cdot m$ 的总和不超过 $10^6$ 。

输出

对于每个测试用例，输出一个数字— $1543$ 按照顺时针的顺序在地毯所有层中出现的总次数。

样例

input

8
2 4
1543
7777
2 4
7154
8903
2 4
3451
8888
2 2
54
13
2 2
51
43
2 6
432015
512034
4 4
5431
1435
5518
7634
6 4
5432
1152
4542
2432
2302
5942

output

1
1
0
1
0
2
2
2

注

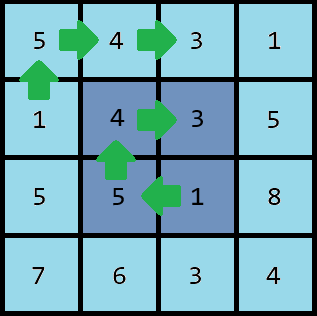
$1543$ 在第七个示例中的出现次数。不同层的颜色不同。

解法

这题目是一个“回”字形循环遍历的问题，可以首先用一个数组将每一层的所有数字先存起来，然后再循环遍历数组就可以了。

对于下标的判断，以及循环的初始条件，结束条件，在这道题显得非常重要。

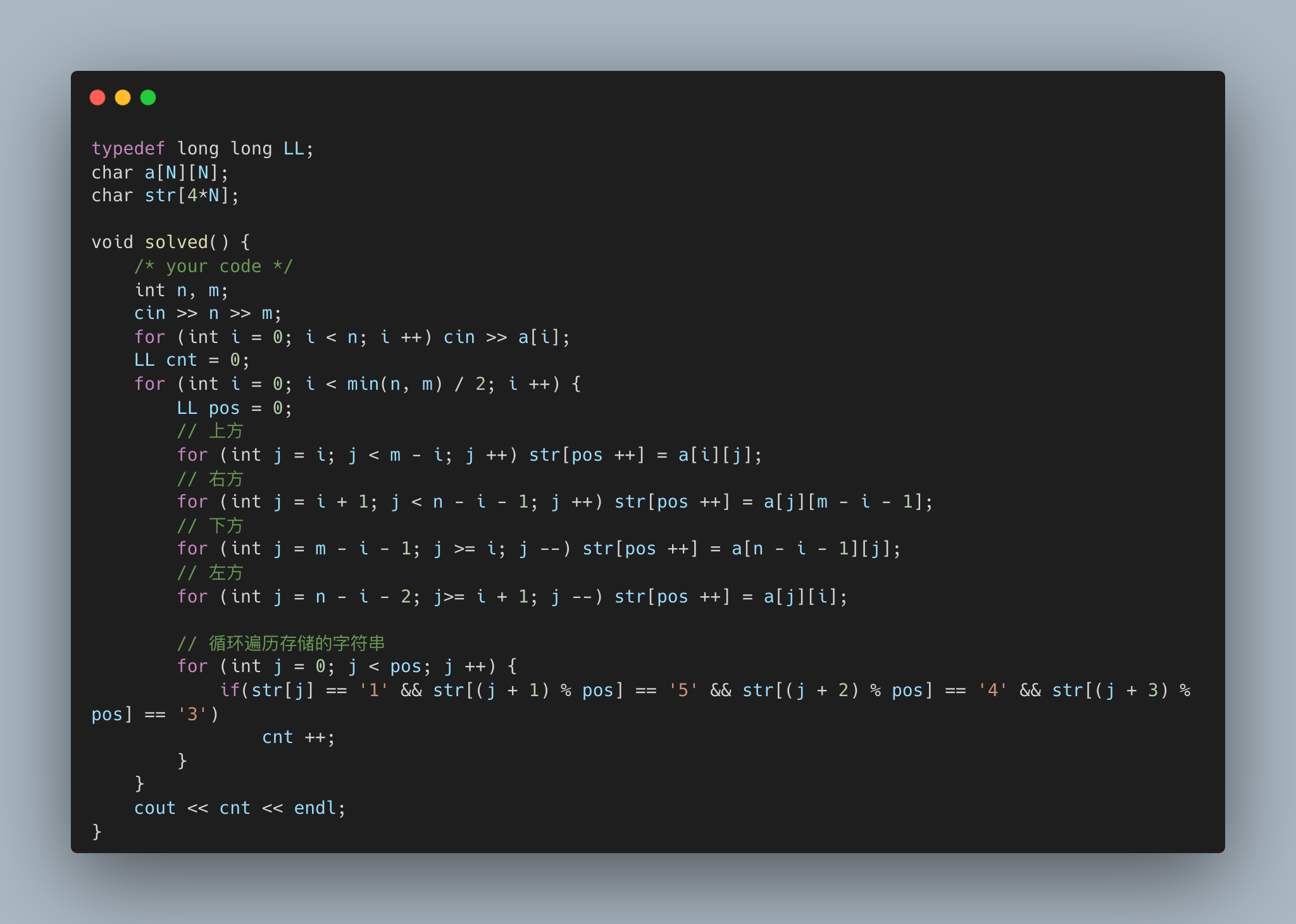
typedef long long LL;
char a[N][N];
char str[4*N];

void solved() {
	/* your code */
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < n; i ++) cin >> a[i];
	LL cnt = 0;
	for (int i = 0; i < min(n, m) / 2; i ++) {
		LL pos = 0;
		// 上方
		for (int j = i; j < m - i; j ++) str[pos ++] = a[i][j];
		// 右方	
		for (int j = i + 1; j < n - i - 1; j ++) str[pos ++] = a[j][m - i - 1];
		// 下方
		for (int j = m - i - 1; j >= i; j --) str[pos ++] = a[n - i - 1][j];
		// 左方
		for (int j = n - i - 2; j>= i + 1; j --) str[pos ++] = a[j][i]; 

		// 循环遍历存储的字符串
		for (int j = 0; j < pos; j ++) {
			if(str[j] == '1' && str[(j + 1) % pos] == '5' && str[(j + 2) % pos] == '4' && str[(j + 3) % pos] == '3')
				cnt ++;
		}	
	}
	cout << cnt << endl;
}

总结

今天的题目主要考察“回”字形遍历数组，难度较易，其中应该注意循环的初始条件和终止条件的判断，最后呢，需要循环遍历存储的数组。