深度学习知识整理---图神经网络（持续更新）

一、图基础知识

1 图的定义

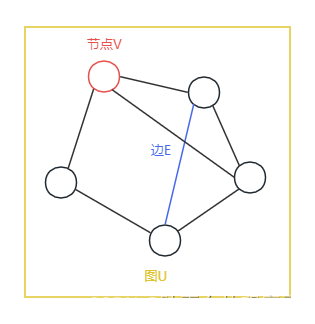
1. 节点：Vertex(Node) contains attributes，节点包含与节点相关的特征

2. 边：Edge(link) contains attributes and direction，边包含与边相关的特征与方向信息

3. 图：Global contains attributes，图包含与图相关的特征

2 邻接矩阵与邻接数组

以上图(无向图)为例，将无向图修改为更加广泛的无向图并给每个节点进行编号，如图所示：

图中共有n个节点，n值为5。

1.邻接矩阵则为n*n的矩阵结构，若i->j存在有向边，那么矩阵(i,j)位置为1，否则为0，如下所示：

节点编号	0	1	2	3	4
0	0	0	0	0	1
1	1	0	0	1	0
2	1	1	0	0	0
3	0	0	1	0	1
4	1	0	0	0	0

2.实际情况中图中边的数量是相对较少的，因此若使用邻接矩阵存储节点间关系会导致大量空间被“无用0”占用，导致存储空间的浪费，因此可以考虑使用邻接数组存储“有用1”的信息，如下所示：

Adjacency List：
[
    [0,1], # 举例：0号节点->1号节点有边
    [1,0],[1,3],
    [2,0],[2,1],
    [3,2],[3,4],
    [4,0]
]

3 图消息传递

图的消息传递也可理解为图中每个节点汇总周围其他节点的信息并对自己进行更新，简单举例如下：

若节点0想要进行消息传递（或称为0号节点想要更新自身信息），需要做两步操作：

1. 保留自身信息

2. 汇集周围信息

具体公式如下所示，其中hi代表i号节点自身信息（或称为各节点的特征向量），W为权重，Ni代表节点i的邻居节点（Neighbor）

二、图卷积网络GCN

1 GCN基本概念

GCN输入：

1. 各节点的输入特征h

2. 网络结构图

GCN天然支持半监督学习：

1. 不需要全部节点都有标签，部分节点有标签就行

2. 计算损失时只用带有标签的节点计算即可

如图所示，红色代表异常，蓝色代表正常，?代表没有标签，可以依靠图的消息传递去得到?最后的输出特征，在半监督学习下，可以只对有标签的（蓝色 and 红色）点计算损失，因为要是想红色 and 蓝色点效果好，其周围点效果应该也要训练好

 

2 GCN计算

注：这里的F（Feature）就是上文的h，即各节点的特征 

# 邻接矩阵A
A = [
        [0,0,0,0,1],
        [0,0,0,1,1],
        [0,0,0,1,1],
        [0,1,1,0,1],
        [1,1,1,1,0]
    ]

# 度矩阵D
D = [
        [1,0,0,0,0],
        [0,2,0,0,0],
        [0,0,2,0,0],
        [0,0,0,3,0],
        [0,0,0,0,4]
    ]
  
# 节点特征矩阵，一行代表一个节点的特征（也可以理解为一行一个样本）
Feature=[
            [-1.1,3.2,4.2],
            [0.4,5.1,-1.2],
            [1.2,1.3,2.1],
            [1.4,-1.2,2.5],
            [1.4,2.5,4.5]
        ]

现在要根据两步（结合自身信息 结合邻居信息）去计算新的特征矩阵Feature，则需要给A邻接矩阵的对角加1

# 对角加1后的邻接矩阵，也可以理解为 自己连自己
A_hat = [
            [1,0,0,0,1],
            [0,1,0,1,1],
            [0,0,1,1,1],
            [0,1,1,1,1],
            [1,1,1,1,1]
        ]

使用新的A_hat与Feature矩阵进行矩阵乘法即可实现 结合自身信息、结合邻居信息

# 注意此处是矩阵乘法，不是点乘
# 结果为5*3的矩阵，也就是说每行(每个节点)有了结合后的新的特征
A_hat*Feature = [
                    [...,...,...],
                    [...,...,...],
                    [...,...,...],
                    [...,...,...],
                    [...,...,...]
                ]

但是，这就导致新的问题：

1. 如果我的某个邻居的Feature的值很高，那么会导致我这行的数都很高（即i行的3个数比其他行的3个数都很高）

2. 如果我的邻居的Feature值不是很高，但是我邻居数量很多很多，这也会导致上述问题

因此，需要对每行进行归一化操作，因此需要应用到新的度矩阵D_hat，D_hat和D相比，对角位置加1，也可以理解为因为A_hat对角加1，导致所有节点的度数加1

D_hat = [
            [2,0,0,0,0],
            [0,3,0,0,0],
            [0,0,3,0,0],
            [0,0,0,4,0],
            [0,0,0,0,5]
        ]

再获取到新的度矩阵D_hat后，即可对行进行归一化

# 左乘D_hat的逆矩阵
(D_hat)^(-1)*A_hat*Feature = [
                                 [1/2,0,0,0,0],
                                 [0,1/3,0,0,0],
                                 [0,0,1/3,0,0],
                                 [0,0,0,1/4,0],
                                 [0,0,0,0,1/5]
                             ]*
                             [
                                 [...,...,...],
                                 [...,...,...],
                                 [...,...,...],
                                 [...,...,...],
                                 [...,...,...]
                             ]
# 取D_hat的逆矩阵就是为了除以度数，即达到求均值的目的

论文中，不仅对行做均值，也对列做均值，因此再在A_hat的右侧也乘以了D_hat的逆矩阵。同时，GCN中在乘以D_hat的逆矩阵时，并未乘以D_hat的-1次幂，而是-1/2次幂，这是为了让对角的信息（也就是自身信息）被归一化一次而不是两次。

问题：那为什么要对行列分别使用度进行归一化呢？重点!!!

原因：可以仔细研究一下，左乘的D_hat的逆是指除以当前行i节点自己的度，右乘的D_hat的逆是指除以当前列j节点自己的度，也就是(i,j)位置的值把当前行i节点的度值与当前列j节点的度值都除以了一次。假设我们只对行做一次归一化，也就是说每行的值只除以当前行i节点的度值，那么就会导致一个很严重的问题，即若i行的度很小（i节点只连1个节点j），而j列的度很大（j节点连接很多很多其他节点），每次每行只除以i节点的度那么就导致i节点学到了很多j节点的信息，而j行j节点只学很少的i。也就是说可能i节点只是穷人因此认识的人少（度数小），而j节点是富人因此认识的人多（度数大），这样学习下去的后果会导致穷人节点i越学习越会被误认为是富人，因为每次学到富人的信息很多，但其实从富人节点j角度，j认识很多人，可能与i只有很少的联系。因此需要行列都要进行归一化，这样的话(i,j)位置就会除以i的度与j的度，这样穷人节点i就不会过多学习富人的特征了。

以上步骤是面向邻接矩阵A，对于Feature矩阵，我们可以使用类似于线性层（W权重）的手段去对Feature的维度进行调整，比如Feature为5*3，W为3*10，这样Feature*W就能够将维度升至10。此外和神经网络类似，GCN中的线性层也可以有多个。

总结，GCN计算公式如下，需要注意：

1. H即为Feature

2. l为迭代次数

三、图注意力网络GAT

1 GAT基本概念

GAT与GCN相比，区别主要在于使用了注意力机制，进而影响邻接矩阵A。具体来讲，GCN中节点i在进行节点更新时邻接矩阵只做了归一化处理，但是实际上其对于邻居节点的信息汇总的权重均为1，并无法体现学习周围节点的不同程度，即无法体现i节点学习j节点信息的0.1、k节点信息的0.6、m节点信息的0.3（举例），因此图注意力网络诞生，使用attention机制。

2 GAT计算

 

GAN如图所示，在图中a0->1，a0->2，a0->4均为注意力系数，即从对应节点学习多少，且a0->1+a0->2+a0->4=1。

接下来说明如何计算注意力系数a，以计算a0->1为例：

1. 已知h0与h1，首先乘以线性层的权重W，得到Wh0与wh1

2. 然后将Wh0与Wh1进行拼接得到Wh，假设Wh维度为n

3. Wh与n*1的向量点乘（向量为可学习的新权重层）得到一个值e

4. 最后e经过ReLU层后保留大于0的数值得到e_hat

5. 计算所有邻居节点的e_hat，并使用softmax函数处理，最终得到每个邻居节点的注意力系数a

6. 进而得到a0->1

 

四、图采样聚合网络GraphSAGE

1 GraphSAGE基本概念

无论是GCN还是GAT，在计算时都要将全图的邻接矩阵加载到内存，然后计算。但有时全图很大，因此会导致无法计算的情况出现，因此GraphSAGE被提出。其思想可以概括为：先采样再聚合。

这里强调一下，阶、层数、跳数是同一概念，以图2为例：

1. 若想要让红色节点聚合1阶的信息（跳数为1的节点信息），那么就是让红色节点聚合所有蓝色节点的信息

2. 若想要让红色节点聚合2阶的信息（跳数为1和跳数为2的节点信息），那么就是让红色节点先聚合蓝色节点的信息得到红色自己的h0，蓝色节点也同时聚合绿色节点的信息得到蓝色自己的h0；然后红色节点再去聚合蓝色节点的h0信息得到红色自己的h1

2 GraphSAGE计算

2.1 邻居节点采样

这里对邻居采样直接上代码：

1. sample函数：对多个节点的邻居进行1阶采样

2. multihop_sampling函数：对多个节点的邻居进行n阶采样

def sample(src_nodes,sample_num,graph):
    # src_nodes：要对哪些节点的邻居进行采样
    # sample_num：对邻居的采样的数量
    # graph：可以理解为邻接数组
    results = []
    
    # 遍历所有的节点
    for id in src_nodes:
        # 这里说的是
        # len(graph[id])：获取当前id节点的邻居数量
        # sample_num为要采样出的邻居数量
        if len(graph[id])>=sample_num：
            # 如果邻居数量超过采样数量，那么就不放回抽样
            res = np.random.choice(graph[id],size=(sample_num,),replace=False)
        else:
            # 否则有放回抽样
            res = np.random.choice(graph[id],size=(sample_num,),replace=True)
        results.append(res)
     return np.asarray(results).flatten()
     
# 测试
sample([1],3,graph) # 代表要对1节点采样3个邻居出来

 

def multihop_sampling(src_nodes,sample_num,graph):
    # src_nodes：要对哪些节点的邻居进行采样
    # sample_num：每阶采样邻居的数量，是list
    # graph：可以理解为邻接数组
    sampling_results = [src_nodes] # 原始要采样邻居的节点是第一层
    
    for k,hopk_num in enumerate(sample_num):
        hopk_result = sample(sampling_results[k],hopk_num,graph)# 对第k层节点采样hopk_num个邻居
        sampling_results .append(hopk_result) # 将第k层采样出来的邻居，放入第k+1层，后面循环对第k+1层的节点的邻居进行采样
        
    return sampling_results
    
# 测试
multihop_sampling([1],[2,3],graph) # 代表对1号节点进行2阶采样，即1号节点要采样2个邻居，1号节点的2个邻居分别要采样3个邻居

2.2 邻居节点聚合

在获取到每个节点采样后的邻居节点后，即可缩小每个节点聚合时的邻接矩阵（其实是换了另一种计算思路），进而对邻居节点信息进行聚合