并查集

普通并查集（朋友的朋友是朋友）

​ 思路：

​ 1.用一个数组 $f$ 表示 $i$ 的上一层是 $f[i]$ ，初始情况下 $f[i]=i$ 全部满足；

​ 2.每当两个点连接时，都可以将其中一个点的 $f$ 值修改为另一个点的 $f$ 值，表示此两点的上一层相同——两个点为同一整体；

​ 3.每次连接时，必须将 $a$ 的最上层 $f$ 值和 $b$ 的最上层 $f$ 值连接，这样 $a$ 、$b$ 以及 $a$、$b$ 过程中连接过得所有点的 $f$ 值都相同，他们都在同一个整体中；

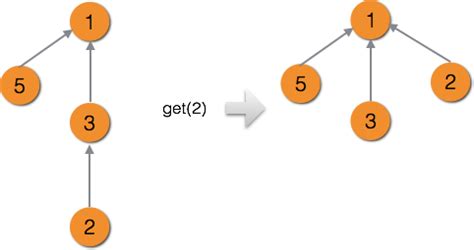
public static int find(int x){
    if(f[x] ！= x)
    	f[x] = find(f[x]);//将过程中的所有点的f值全部赋值为顶点的f值
    return f[x];
}

public static void merge(int x,int y){
    int xx = find(x);
    int yy = find(y);
    if(xx!=yy)
        f[yy] = xx;
}

例题：蓝桥幼儿园

题目链接：蓝桥幼儿园 - 蓝桥云课 (lanqiao.cn)

​ 思路：用 $f$ 数组表示关系，如果 $op$ 为 $1$ ，便进行 $merge$ 操作，如果 $op$ 为 $2$ ，判断两个学生的 $f$ 值是否相同。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class Main {
	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int[] p;//p[i]表示i的头结点是p[i]
	public static void main(String[] args) throws IOException{
		String[] s = in.readLine().split(" ");
		int n = Integer.parseInt(s[0]);
		int m = Integer.parseInt(s[1]);
		p = new int[n+1];
		for(int i=1;i<=n;i++) {
			p[i] = i;//第i个小朋友的根节点
		}
		for(int i=0;i<m;i++) {
			s = in.readLine().split(" ");
			int op = Integer.parseInt(s[0]);
			int x = Integer.parseInt(s[1]);
			int y = Integer.parseInt(s[2]);
			if(op==1) 
				merge(x,y);
			else 
				System.out.println(find(x)==find(y)?"YES":"NO");
		}
    }
    static int find(int x) {
        if(p[x]!=x)
            p[x]=find(p[x]);
        return p[x];
    }
    static void merge(int x,int y){
        int xx = find(x);
        int yy = find(y);
        if(xx != yy)
            f[yy] = xx;
    }
}

种类并查集（敌人的敌人是朋友）

​ 思路：

​ 1.在普通并查集的基础上进行完善，如果 $a$ 和 $b$ 是敌人，$b$ 和 $c$ 是敌人，那么 $a$ 和 $c$ 是朋友，这时可以表示为：$a$ 和 $!b$ 是朋友，$b$ 和 $!a$ 是朋友，$c$ 和 $!b$ 是朋友，$b$ 和 $!c$ 是朋友；

​ 2.数组 $f$ 的大小需要为普通并查集的二倍，前半部分表示 $i$ 的 $f[i]$ 值，后半部分表示 $!i$ 的 $f[i]$ 值；

例题：蓝桥侦探

题目链接：蓝桥侦探 - 蓝桥云课 (lanqiao.cn)

​ 思路：

​ 1.种类并查集，如果 $a$ 和 $b$ 不在一起， $b$ 和 $c$ 不在一起，那么 $a$ 和 $c$ 一定在一起，否则，有人说谎；

​ 2.题目输入 $x$，$y$ 表示 $x$ 和 $y$ 不在一起，那么便可以表示为：$x$ 和 $!y$ 在一起，$y$ 和 $!x$ 在一起，两个内容都进行 $merge$ 操作；

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
	static int[] f;
	public static void main(String[] args) throws IOException{
		String[] s = in.readLine().split(" ");
		int n = Integer.parseInt(s[0]);
		int m = Integer.parseInt(s[1]);
		f = new int[2*n+2];
		for(int i=0;i<2*n+2;i++) {
			f[i] = i;
		}
		for(int i=0;i<m;i++) {
			s = in.readLine().split(" ");
			int x = Integer.parseInt(s[0]);
			int y = Integer.parseInt(s[1]);
			if(find(x)!=find(y)) {
				merge(x, y+n);
				merge(x+n, y);
			}else {
				System.out.println(x);
				return;
			}
		}
	}
	static int find(int x) {
		if(f[x]!=x)//夫点不是自己
			f[x]=find(f[x]);
		return f[x];
	}
	static void merge(int x,int y) {
		x = find(x);
		y = find(y);
		f[y] = x;
	}
}

带全并查集

​ 思路：在普通并查集的基础上还需要记录长度。

例题：蓝桥部队

题目链接：蓝桥部队 - 蓝桥云课 (lanqiao.cn)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

public class Main {
	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
	static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
	static int[] f;//存放此列的排头元素
	static int[] length;//存放此列的军人数量
	static int[] num;//此军人前面有多少人
	public static void main(String[] args) throws IOException{
		String[] s = in.readLine().split(" ");
		int n = Integer.parseInt(s[0]);
		int m = Integer.parseInt(s[1]);
		f = new int[n+1];
		length = new int[n+1];
		num = new int[n+1];
		for(int i=1;i<=n;i++) {
			f[i] = i;
			length[i] = 1;
		}
		for(int i=0;i<m;i++) {
			s = in.readLine().split(" ");
			int op = Integer.parseInt(s[0]);
			int x = Integer.parseInt(s[1]);
			int y = Integer.parseInt(s[2]);
			if(op==1) {//合并x和y所在列 x到y后面 
				merge(x, y);
			}else {//求x和y间隔
				if(find(x)!=find(y)) {
					System.out.println(-1);
				}else {
					System.out.println(Math.abs(num[x]-num[y])-1);
				}
			}
		}
	}
	static void merge(int x,int y) {
		x = find(x);
		y = find(y);
		if(x==y)
			return;
		num[x] = num[x] + length[y];
		length[y] = length[y] + length[x];
		f[x] = y;
	}
	static int find(int x) {
		if(x!=f[x]) {
			int root = find(f[x]);
			num[x] = num[x] + num[f[x]];
			return f[x] = root;
		}
		return f[x];
	}
}