
原文信息(包括题目、发表期刊、原文链接等):Linear convergence of first order methods for non-strongly convex optimization
原文作者:I. Necoara, Yu. Nesterov, F. Glineur
论文解读者:陈宇文
编者按:
传统的一阶算法在强凸条件下是可以得到线性收敛速率的,但是非强凸条件下只有次线性收敛速率。近年来,最新的研究表明在某些特殊条件下,一阶算法的线性收敛速度仍然成立。本文将基于发表于Mathematical Programming上的Linear convergence of first order methods for non-strongly convex optimization一文[1]详细介绍有哪些非强凸条件可以使得一阶算法的收敛速率成立。
一、传统的一阶算法收敛速度
在对于一阶算法进行收敛性分析时,传统的一阶算法在强凸条件下是可以得到线性收敛速率的,但是非强凸条件下只有次线性收敛速率。对于一个在XXX集合上的凸优化问题
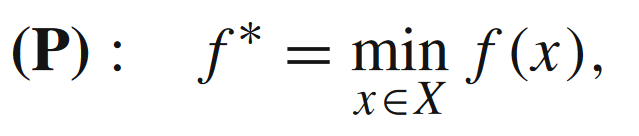
最常见的一阶算法是梯度下降法(GM),

最常见的加速方法是动量加速法(FGM),

这两个算是优化算法领域最经典的算法,算法收敛速度取决于函数f(x)f(x)f(x)的光滑性和强凸性:
- 当f(x)f(x)f(x)是LfL_fLf光滑时,即
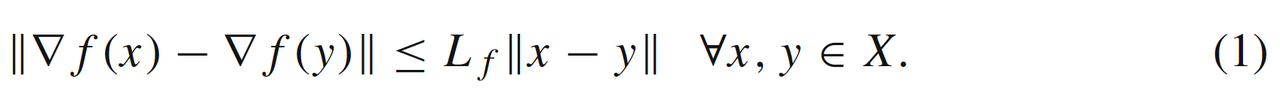
此时GM和FGM的收敛速率为次线性,依次为O(1/k)O\left({1}/{k}\right)O(1/k)和O(1/k2)O\left({1}/{k^2}\right)O(1/k2):
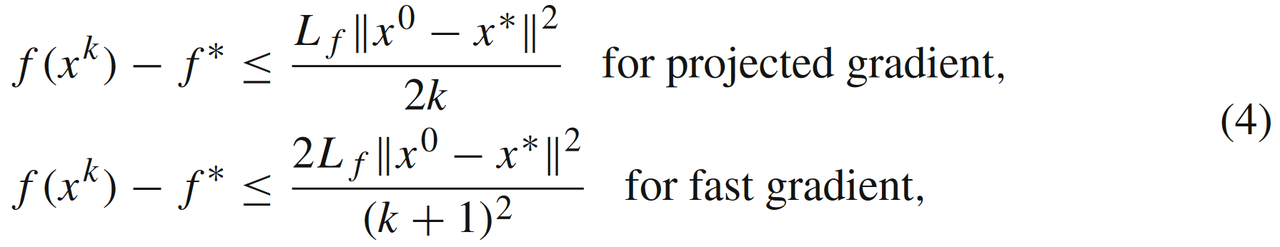
- 当f(x)f(x)f(x)是LfL_fLf光滑同时又满足σf\sigma_fσf强凸条件(我们称之为问题SLf,σf(X)\mathbf{S_{L_f,\sigma_f}(X)}SLf,σf(X)),即满足如下的(等价)强凸条件
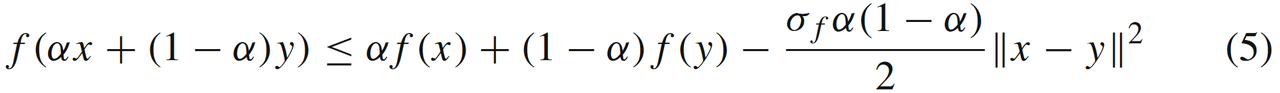
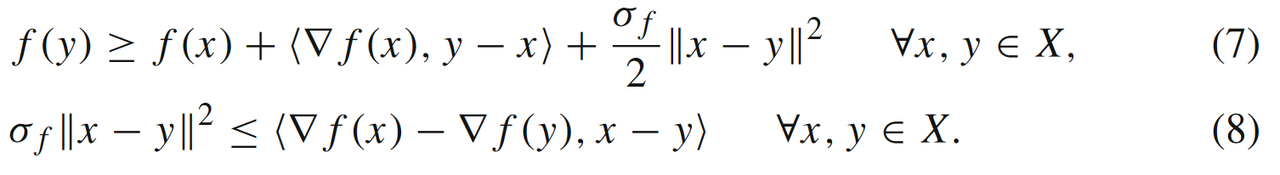
此时GM和FGM的收敛速度可以被提升到线性收敛,
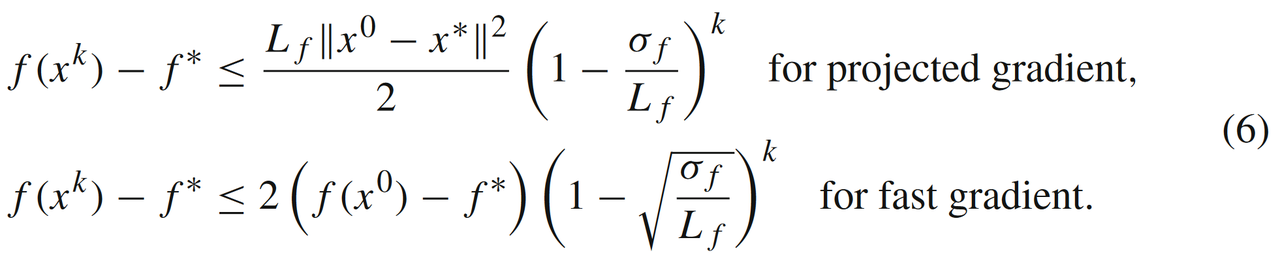
可以发现线性收敛速度取决于强凸条件σf\sigma_fσf参数(见公式(6))。那如果函数f(x)f(x)f(x)要是不满足强凸条件((5)或者(7)-(8)),我们是否能根据某些更弱的条件推出一阶算法的线性收敛速率?
我们首先定义梯度映射g(x)g(x)g(x)为
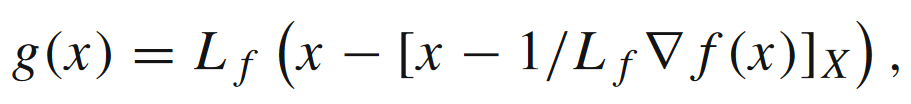
这个可以看成是根据相邻两个周期的xxx(基于投影梯度下降算法)做位移的近似。
根据强凸条件,我们可以得到如下的不等式
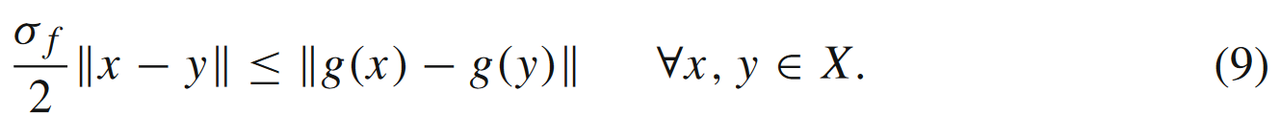
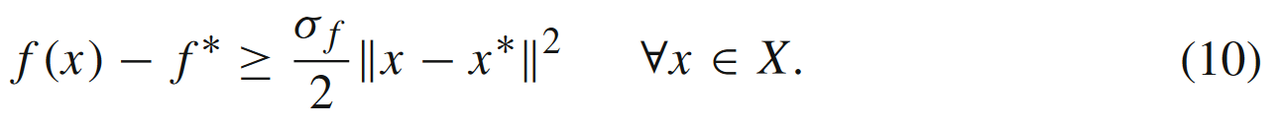
这将在接下来的分析中起着关键作用。
二、其他有用的非强凸条件
相较于强凸条件((5),(7)或者(8)),文中介绍了5种新的松弛条件。在之后的介绍中,我们都默认fff是LfL_fLf光滑的函数。
2.1 拟强凸模型
假设在强凸条件(7)中,我们取近似点y=xˉ≡[x]X∗y=\bar{x} \equiv [x]_{X^*}y=xˉ≡[x]X∗,则可以得到拟强凸模型qSLf,κf(X)\mathit{q}S_{L_f,\kappa_f}(X)qSLf,κf(X):
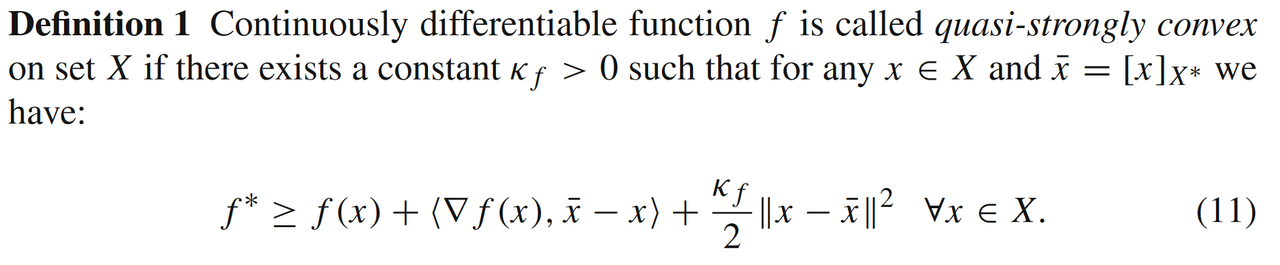
2.2 二次下估计模型
假设在强凸条件(7)中,我们取近似点y=x,x=xˉ≡[x]X∗y=x, x=\bar{x} \equiv [x]_{X^*}y=x,x=xˉ≡[x]X∗,则可以得到二次下估计模型ULf,κf(X)U_{L_f,\kappa_f}(X)ULf,κf(X):

此时条件数μf=κf/Lf∈(0,1]\mu_f = \kappa_f/L_f \in (0,1]μf=κf/Lf∈(0,1]。
2.3 二次梯度增长模型
把公式(11)和(14)相加,则可以得到二次增长型条件GLf,κf(X)G_{L_f, \kappa_f}(X)GLf,κf(X):

2.4 二次增长函数模型
熟悉凸优化的同学应该知道一阶最优条件
⟨∇f(x∗),y−x∗⟩≥0,∀y∈X,x∗∈X∗.\langle \nabla f(x^*), y - x^* \rangle \ge 0, \forall y \in X, x^* \in X^*.⟨∇f(x∗),y−x∗⟩≥0,∀y∈X,x∗∈X∗.
假设我们不考虑一阶部分在强凸条件(7)中的作用,同时公式(7)中带入y=x,x=xˉ≡[x]X∗y=x, x=\bar{x} \equiv [x]_{X^*}y=x,x=xˉ≡[x]X∗,则可以得到二次增长型条件FLf,κf(X)F_{L_f, \kappa_f}(X)FLf,κf(X):

2.5 各类条件的强弱关系
需要注意的是,如上的4种条件都不需要函数是凸的!!!这些关系的强弱程度在文中的定理4和图1中可见:

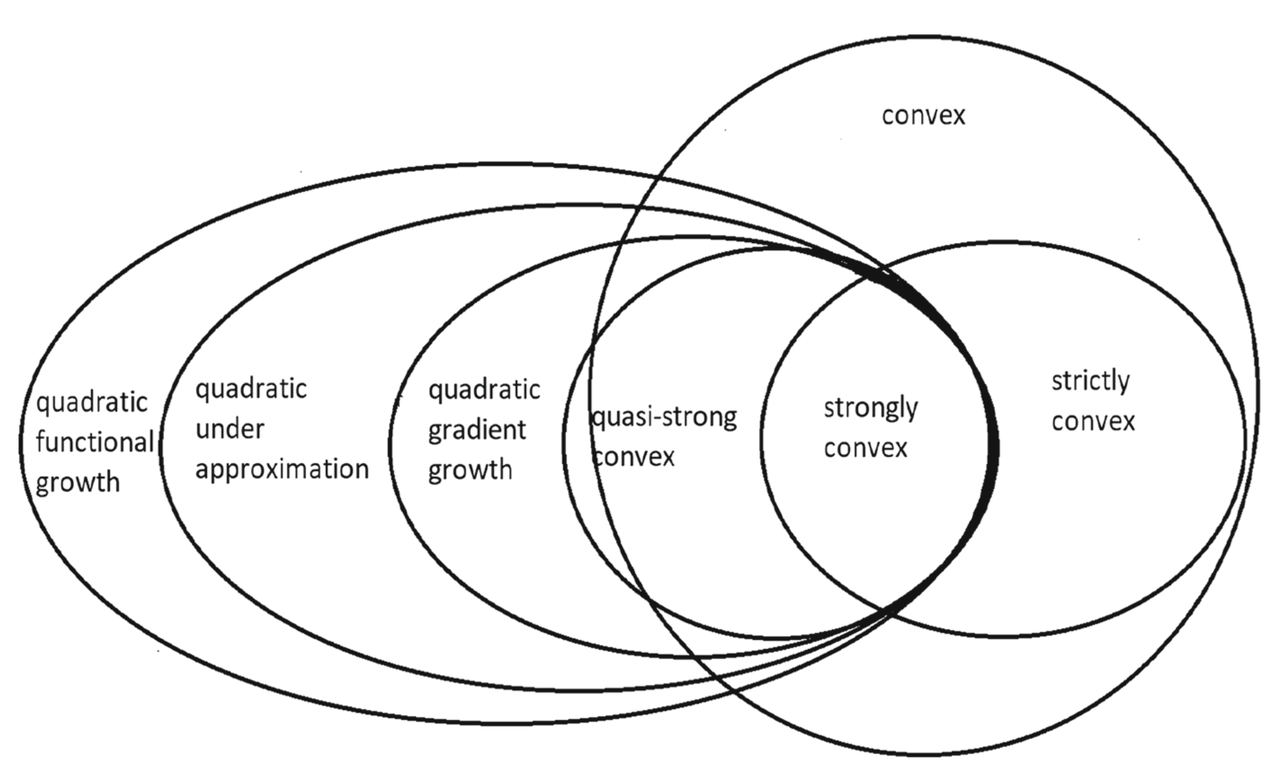
图1:各类条件之间的包含关系图
可以看出强凸条件(7)的条件最强,而二次函数增长条件(23)最弱。
对于投影梯度下降算法
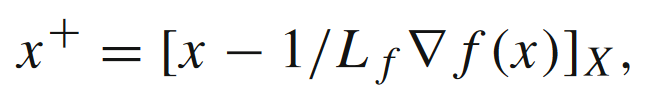
假设x+x^+x+在最优解集合X∗X^*X∗上面的结果xˉ+=[x+]X∗\bar{x}^+ = [x^+]_{X^*}xˉ+=[x+]X∗。如果能够证明每次迭代之后,x+x^+x+相对于X∗X^*X∗的距离要比xxx更近,那么可以证明函数fff本身是二次增长型条件FLf,κf(X)F_{L_f, \kappa_f}(X)FLf,κf(X):

2.6 误差边界条件
除此之外,文中还介绍了基于梯度映射
g(x)=Lf(x−x+)g(x) = L_f(x-x^+)g(x)=Lf(x−x+)
有关的误差边界条件。可以知道在最优解x∗x^*x∗时g(x∗)=0g(x^*)=0g(x∗)=0,当问题是无约束优化(X=RnX = \mathbb{R}^nX=Rn)时,g(x)=∇f(x)g(x) = \nabla f(x)g(x)=∇f(x)。对于梯度LfL_fLfLipschitz连续时,我们有
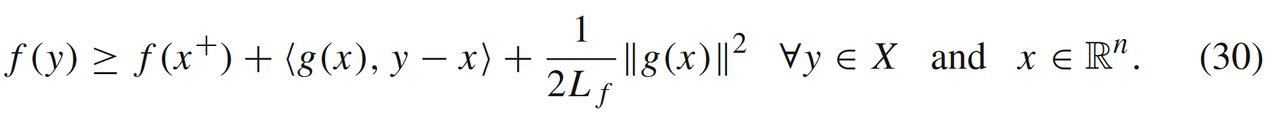
公式(30)中取y=xˉy=\bar{x}y=xˉ和f(x+)≥f∗f(x^+) \ge f^*f(x+)≥f∗可以得到
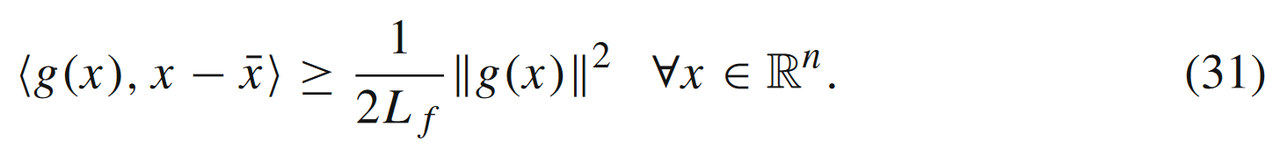
文中进一步定义了全局误差边界条件εLf,κf(X)\varepsilon_{L_f,\kappa_f}(X)εLf,κf(X):

此时条件数μf=κf/Lf∈(0,2]\mu_f = \kappa_f/L_f \in (0,2]μf=κf/Lf∈(0,2]。文中定理6和定理7证明了误差边界条件εLf,⋅(X)\varepsilon_{L_f,\cdot}(X)εLf,⋅(X)和二次增长型条件FLf,⋅(X)F_{L_f, \cdot}(X)FLf,⋅(X)是相互包含的关系:
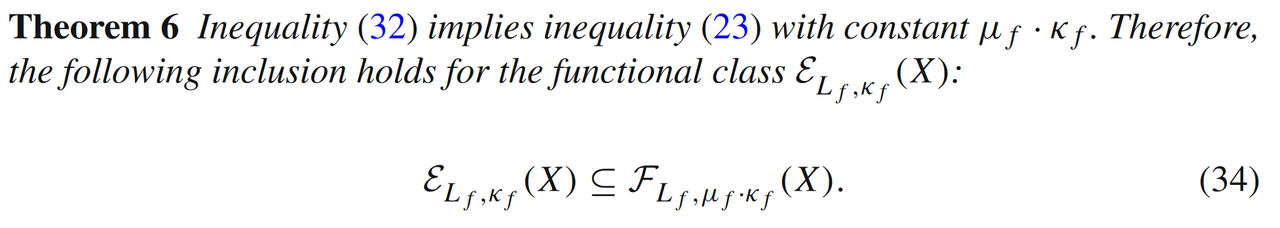
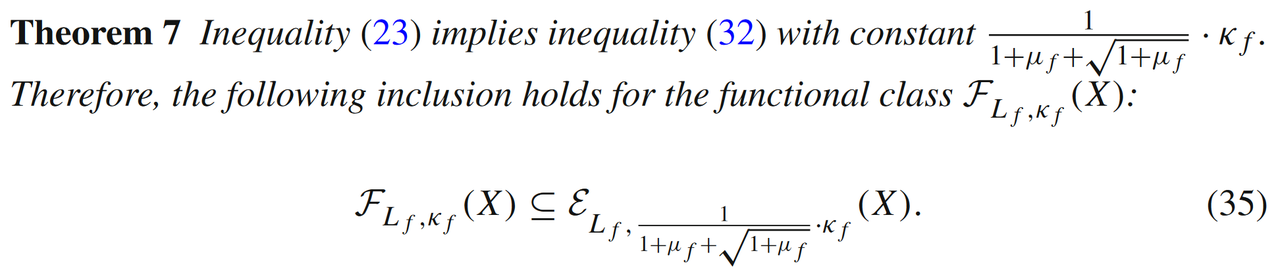
三、函数实例分析
对于上一节介绍的几种松弛强凸条件,文中也列举了几个相关的问题模型,问题的约束条件都是线性的,即可表示成多面体
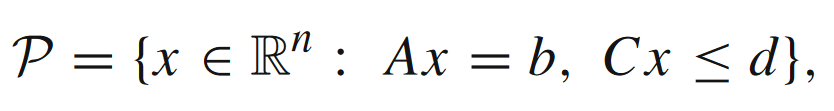
的形式。对于多面体P\mathcal{P}P,一定存在Hoffman常数θ(A,C)>0\theta(A,C) > 0θ(A,C)>0,满足如下不等式
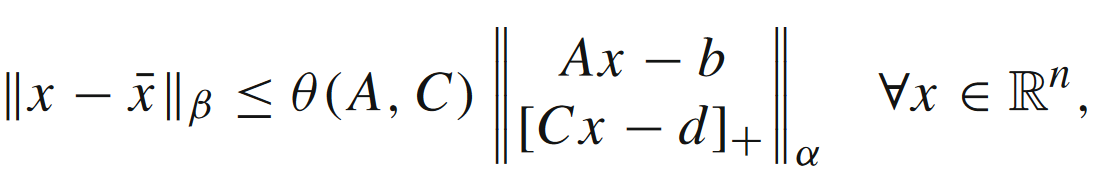
上式可以理解为,现有点xxx与最优集合X∗X^*X∗的距离是被xxx与多面体P\mathcal{P}P的距离控制住的(详情可见文献[2])。对于α=β=2\alpha=\beta=2α=β=2的情形,Hoffman常数θ(A,C)\theta(A,C)θ(A,C)满足
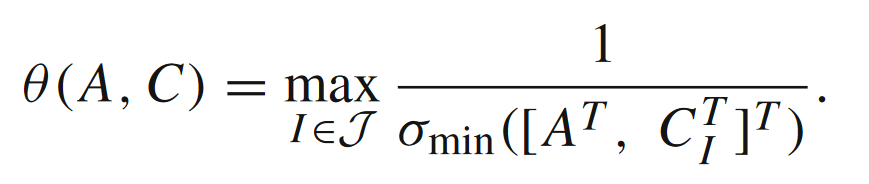
其中r=rank[A⊤,C⊤]r = \text{rank}[A^\top,C^\top]r=rank[A⊤,C⊤],
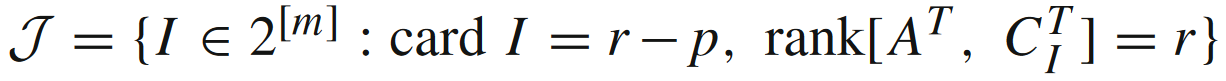
文中考虑了三种模型,都是函数有非满秩的二次惩罚项:
3.1 数学模型
模型1:
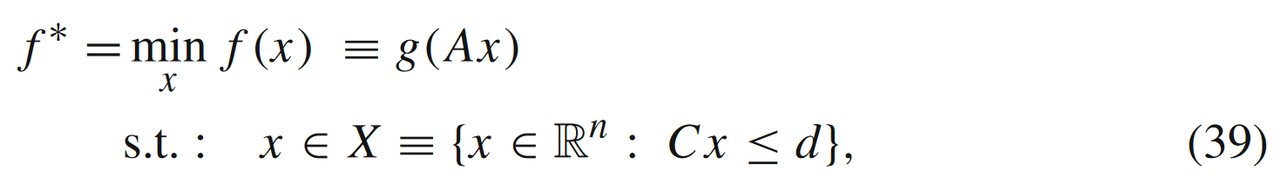
其中,ggg是强凸且光滑的函数,且A∈Rm×nA \in \mathbb{R}^{m \times n}A∈Rm×n。当AAA列满秩时,(39)是强凸函数。当AAA不是列满秩时,则有:
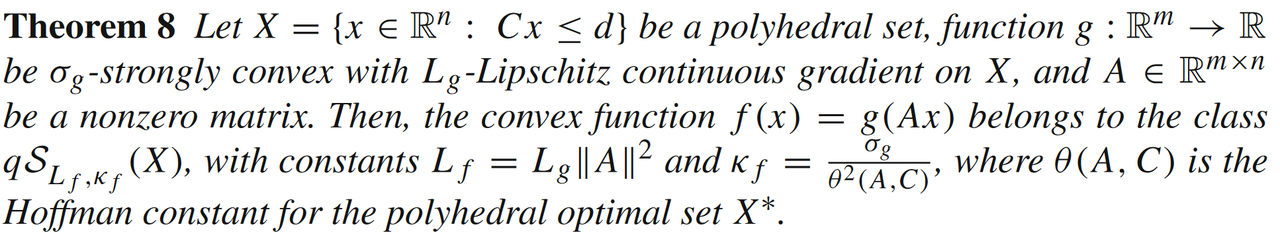
模型2:
当添加线性损失函数c⊤xc^\top xc⊤x但是无约束条件时,即
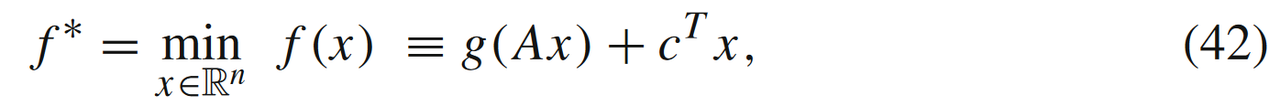
则有
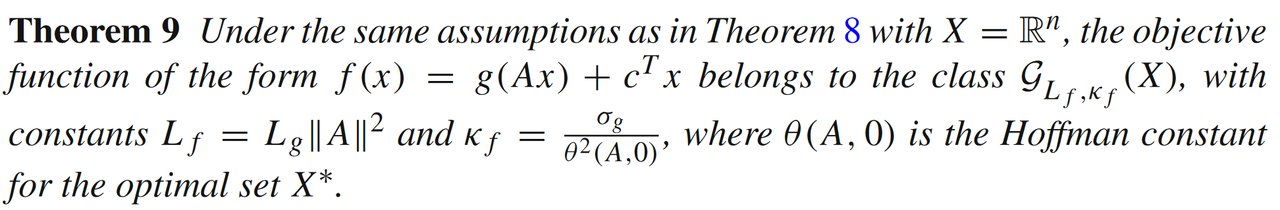
模型3:
相较于(42),当有线性约束条件时,即
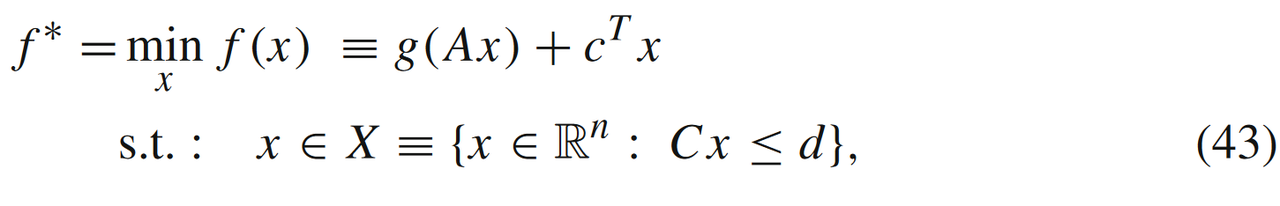
我们需要假设函数fff有一定的上界MMM(有界性),才能满足

可以发现,这三种问题都要求存在二次型损失函数(不需要满秩)部分。
另外再回过头看定理10,如果考虑映射A=IA = IA=I,那么公式(43)中的目标函数就是σg\sigma_gσg强凸的。因为(类)强凸性系数σg≥κf\sigma_g \ge \kappa_fσg≥κf(定义在定理10中的κf\kappa_fκf),所以我们可以发现通过松弛条件(定理10)得到的线性收敛速率要弱于强凸条件(7)下得到的线性收敛速率。
3.2 应用实例
对于上述几类问题模型,文中也给出了几个应用实例,例如Lasso问题和经典的线性规划问题:
Lasso问题
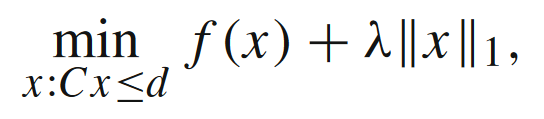
当f(x)=g(Ax)+c⊤xf(x) = g(Ax) + c^\top xf(x)=g(Ax)+c⊤x且ggg是强凸且光滑的函数时,如果重新定义$\mathbb{x} = [x_+ - x_-] ,那么问题可以转化成经典的QP问题,满足前面模型3,即,那么问题可以转化成经典的QP问题,满足前面模型3,即,那么问题可以转化成经典的QP问题,满足前面模型3,即f \in F_{L_f, \kappa_f}(X)$。
线性规划
线性规划问题(K=R+N\mathcal{K} = \mathbb{R}_+^NK=R+N)
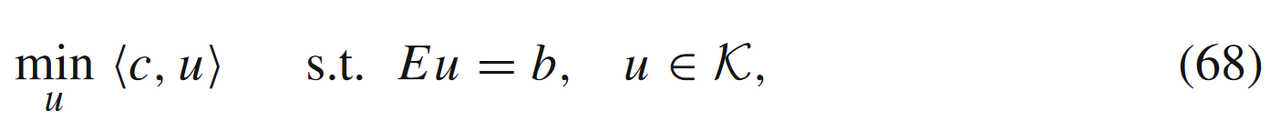
的最优性KKT条件为
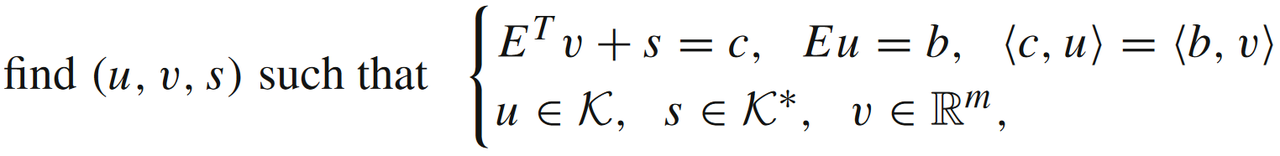
可以同时写成
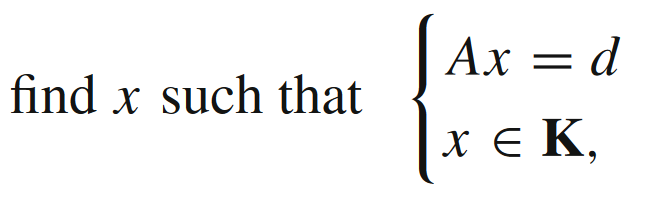
其中
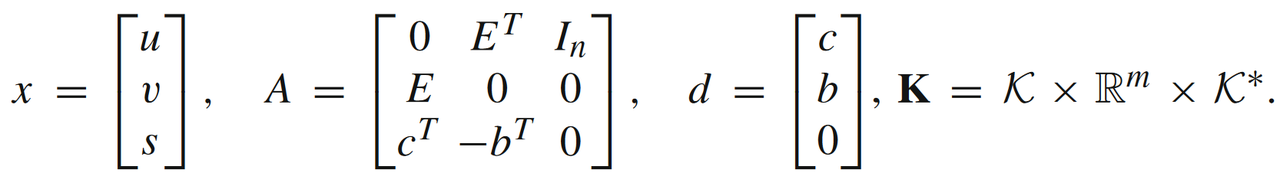
可以把上述寻找可行解问题转换成一个QP问题:

此时(71)满足模型1,f(x)=g(Ax),g(x)=∣∣x−d∣∣2f(x)=g(Ax), g(x)= ||x-d||^2f(x)=g(Ax),g(x)=∣∣x−d∣∣2。
五、其他算法在非强凸条件下收敛性分析
对于第二部分中讨论的几种非强凸条件,文中证明了梯度下降算法(GM)是可以保证线性收敛的:

而对于动量加速法(FGM),文中只证明对于拟强凸模型qSLf,κf(X)\mathit{q}S_{L_f,\kappa_f}(X)qSLf,κf(X),可以获得加速线性收敛速度


除此之外,文中还分析了重启动梯度下降(restarted fast gradient descent)和非精确梯度下降(inexact gradient descent)相关的线性收敛性分析,感兴趣的同学可以阅读原文[1]。
小结
文章中提出了好几种相比于强凸条件的松弛,其中最值得注意还是二次增长型条件FLf,κf(X)F_{L_f, \kappa_f}(X)FLf,κf(X)和全局误差边界条件εLf,κf(X)\varepsilon_{L_f,\kappa_f}(X)εLf,κf(X)。个人觉得这些松弛条件是一种相比于强凸条件不同的分析视角:强凸条件考虑的是函数f(x)f(x)f(x)的全局特征(∀x,y∈X\forall x, y \in X∀x,y∈X),而这些松弛条件刻画了迭代变量xxx与最优解集合X∗X^*X∗之间的几何关系(∀x∈X,∀y∈X∗\forall x \in X, \textcolor{red}{\forall y \in X^*}∀x∈X,∀y∈X∗)。
另外对于线性约束条件(多面体P\mathcal{P}P),一阶算法线性收敛速度与多面体的Hoffman常数θ(A,C)\theta(A,C)θ(A,C)相关,而这又和矩阵A,CA,CA,C的奇异值相关,这个也比较符合大家的直觉(约束条件越规则的几何形状,算法收敛速度越快)。
同时需要注意,(11), (14), (18)和(23)这些条件都不需要fff是凸函数,所以文中几类非强凸松弛条件对于非凸问题收敛性的研究也具有重要意义。
最近几年已经有很多关于非强凸但线性收敛的一阶算法研究,例如半正定规划转换为非凸问题后的局部线性收敛性质[3],一阶算法PDHG基于sharpness(公式(23)中的二次项变成一次项)的线性收敛性[4],也希望感兴趣的同学能在这个有趣的领域添砖加瓦。
[1] Necoara, I., Nesterov, Y. & Glineur, F. Linear convergence of first order methods for non-strongly convex optimization. Math. Program. 175, 69–107 (2019).
[2] Hoffman, A.J.: On approximate solutions of systems of linear inequalities. J. Res. Natl. Bur. Stand. 49(4), 263–265 (1952)
[3] Erdogdu, M.A., Ozdaglar, A., Parrilo, P.A. et al. Convergence rate of block-coordinate maximization Burer–Monteiro method for solving large SDPs. Math. Program. 195, 243–281 (2022).
[4] Applegate, D., Hinder, O., Lu, H. et al. Faster first-order primal-dual methods for linear programming using restarts and sharpness. Math. Program. 201, 133–184 (2023).




 文章详细探讨了一阶算法在非强凸优化问题中的线性收敛性,介绍了多种非强凸条件,如拟强凸模型、二次下估计模型等,以及它们与线性收敛速度的关系。研究指出,线性收敛速度与函数的几何特性及约束条件密切相关。
文章详细探讨了一阶算法在非强凸优化问题中的线性收敛性,介绍了多种非强凸条件,如拟强凸模型、二次下估计模型等,以及它们与线性收敛速度的关系。研究指出,线性收敛速度与函数的几何特性及约束条件密切相关。
















 2254
2254

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








