树形DP介绍+经典例题HDU2196_一棵有根树,根结点的编号是1,对其中的任意一个节点,求离它最远的节点的距离-优快云博客

本文介绍了树形动态规划（Tree DP）的概念及其应用，以HDU2196题为例，展示了如何利用树形DP解决寻找树中任意节点到最远节点距离的问题。通过将无根树转化为有根树，使用两个DFS分别计算节点在子树内的最大距离和沿着父节点路径的最大距离，从而避免了超时。最后，通过比较两种情况的最大距离得到最终答案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

树形DP是指在'树'上进行DP，通常用于解决规模较大，如果枚举会TLE，贪心不能得到最优解的问题。由于树有子结构的性质，具有递归性，因此树形DP的状态转移方程非常直观。

树形DP一般会用到以下几点：

1.常用vector建立关系树

2.用DFS从根结点开始记忆化搜索

3.状态转移方程

例题HDU 2196

https://acm.hdu.edu.cn/showproblem.php?pid=2196

题目大意为有一颗树，根结点的编号是1，对其中的任意一个结点，求离它最远的结点的距离。

分析，题目给的是一个无根树，从一个结点出发，做一次BFS找到最长距离复杂度为O(n)，n个结点是O( $n^{2}$ )，显然会TLE。运用树形DP的思维，把无根树转化为有根树(如图)，这样就需要两个DFS来算出。

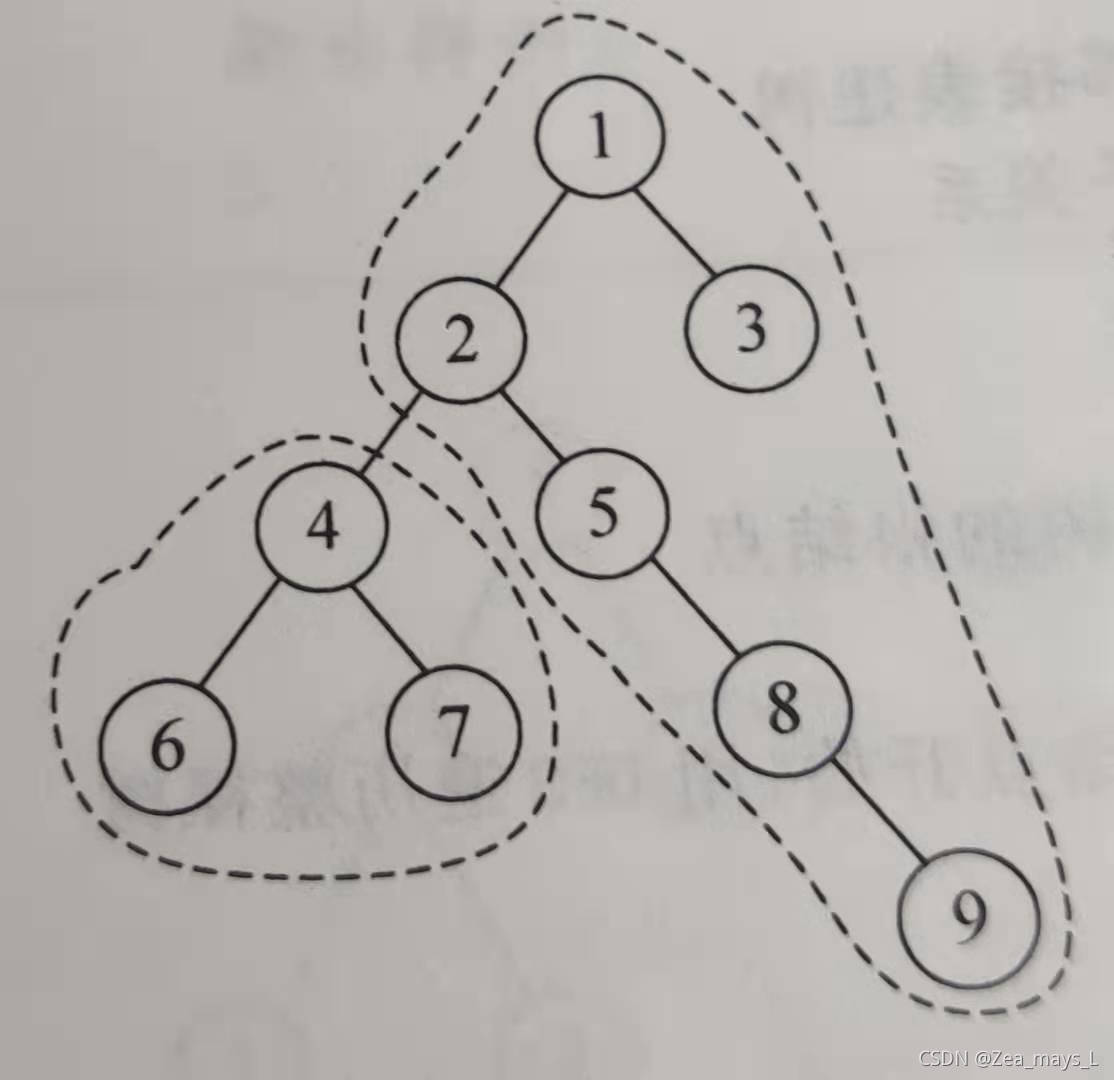
以节点4位例，它的最长距离分两种情况讨论。第一种是节点4在子树中的最大距离L1(对应图中左边圈的部分)，可以通过DFS求出所有节点的最大距离dp[i][0]和次最大距离dp[i][1](如果节点i的最大距离经过第二个子节点，则次最大距离是不经过第二个子节点的最大距离)。第二种是节点4往父节点方向的最大距离L2(对应图中右边圈的部分),L2=父节点2的最大距离+dist(2,4) (结点2,4的距离)，而父节点2的最大距离有两种情况：一种是节点4在父节点的最长子树上，此时L2=次最大距离+dist(2,4)。一种是节点4不在父节点的最长子树上，此时L2=最大距离+dist(2,4)。最后比较L1和L2的大小即可得到答案。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int MAX = 10100;
struct Node {
	int id,cost; //子结点的编号，子结点到父结点的距离大小 
};
vector<Node>tree[MAX];
int dp[MAX][3]; //0为最大距离，1为次最大距离，2位从该结点往上走的最大距离
int n;
void init() {     //初始化+读取数据
	for (int i = 1; i <= n; i++) tree[i].clear();
	memset(dp, 0, sizeof(dp));
	for (int i = 2; i <= n; i++) {
		int x, y;
		cin >> x >> y;
		tree[x].push_back({ i,y });
	}
}

void dfs1(int fa) {   //先处理子结点，再处理结结点
	int one = 0, two = 0; //记录最大距离和次最大距离
	for (int i = 0; i < tree[fa].size(); i++) {
		Node son = tree[fa][i];
		dfs1(son.id);  //递归到底层
		int cost = dp[son.id][0] + son.cost; 
		if (cost >= one) {  //更新
			two = one;
			one = cost;
		}
		if (cost<one && cost>two) {
			two = cost;
		}
	}
	dp[fa][0] = one;
	dp[fa][1] = two;
}

void dfs2(int fa) {  //先处理父结点，再处理子结点
	for (int i = 0; i < tree[fa].size(); i++) {
		Node son = tree[fa][i];
		if (dp[son.id][0] + son.cost == dp[fa][0]) //son在最大距离上时
			dp[son.id][2] = max(dp[fa][2], dp[fa][1]) + son.cost;
		else                                       //son不在最大距离上时
			dp[son.id][2] = max(dp[fa][2], dp[fa][0]) + son.cost;
		dfs2(son.id);
	}
}
int main() {
	while (~scanf("%d",&n)) {
		init();
		dfs1(1);  //得到所有结点的dp[][0],dp[][1]
		dp[1][2] = 0; //节点1为根结点，往上没有结点
		dfs2(1);  //得到所有结点的dp[][2]
		for (int i = 1; i <= n; i++) {
			printf("%d\n", max(dp[i][0], dp[i][2]));
		}
	}
	return 0;
}