matlab的求解方程组函数solve、dsolve、ode系列

一.求解方程组函数：solve

示例：求解含有参数的方程组  ax+by=10.ax-by=20

编程实现：

syms a b x y;
s=solve(a*x+b*y==10,a*x-b*y==20,x,y);
sol_x=s.x
sol_y=s.y

sol_x =
 
15/a
 
 
sol_y =
 
-5/b

二.求解微分方程：dsolve

1. 用字符串描述微分方程及其初始条件；

2. 导数的表示规则：以未知函数y为例,“Dy”表示 对y的1阶导数，“D2y”表示对y的2阶导数，其他各阶导数类似.

示例：

 

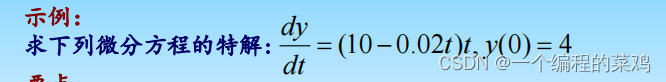
示例1：

syms y t;
ans=dsolve('Dy=(10-0.02*t)*t','y(0)=4',t)

ans =
 
4 - (t^2*(t - 750))/150



示例二：

三.求解微分方程的ode23函数

 

 

 

 

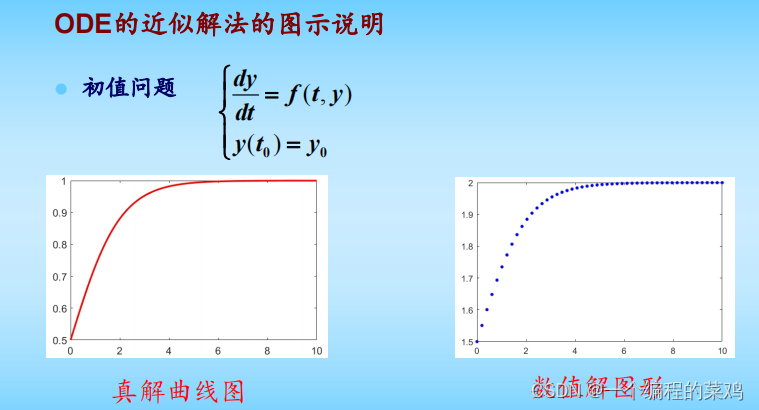
 示例如下：

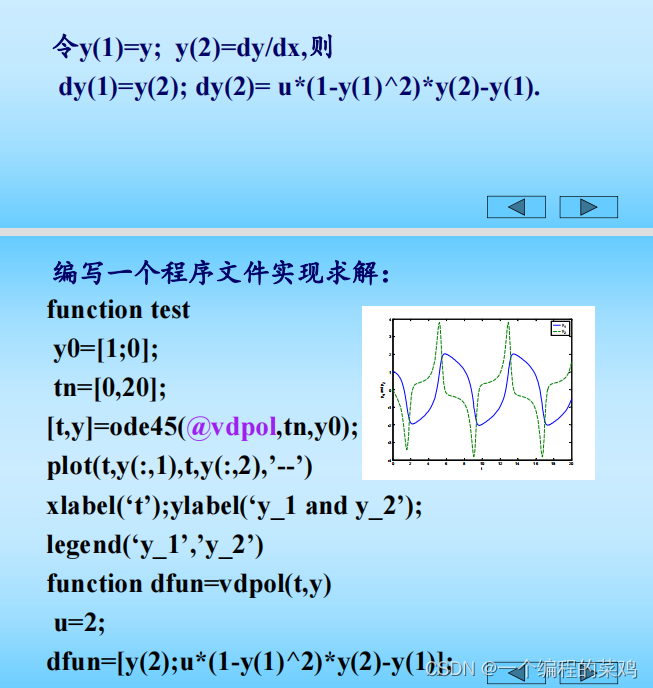
 代码如下：

function qiujiefangcheng=myfun
y0=[0;2];
tspan=[0,3];%求解的范围
[t,y]=ode23(@fun,tspan,y0)




function  dfun=fun(t,y)
dfun=[-exp(1-t)*y(1)+0.8*y(2);
    y(1)-y(2).^3]

代码如下：