数据结构的小理解

数据结构意义：

在有限的空间里规划较大的数据量

1.时间复杂度：

x>1,x足够大的时候，要想达到某个操作数据（增删改查）的目的，所需要的计算次数就是时间复杂度

=>; 代表箭头，推导出的意思

y=ax   = >   o(n)

y=ax+b    =>    o(n) (数据够大，常数可忽略)

y=ax^2+bx+c     =>     o(n^2)

时间复杂度就看x的最高次幂，就是0(n^N)

a^y=x    =>    y=logax   =>   o(logn)

y=a    =>    o(1)

时间复杂度的大小比较

o(1)<o(logn)<o(n)<o(nlogn)<o(n^2)<.....

o(1)经常运用在搜索编号的数组中

o(n)是一 一做比较

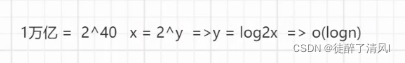
o(logn)比o(n)快很多

2.常见的数据结构

数组 ( 有序，无序)

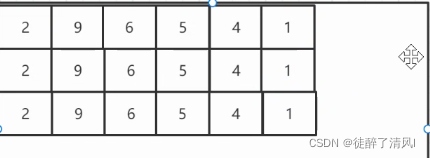
链表（有序，无序） 为了解决数组浪费情况而出现

栈（杯子 一个口）能够快速的增加，删除功能（都是o(1)级别）

队列（水管 两个口）能够快速的增加，删除功能

树（有序，无序）

无序树：

完全树 ：除了最后一层子节点可以不满且靠左的，其他层都是满的（从上到下，从左到右）

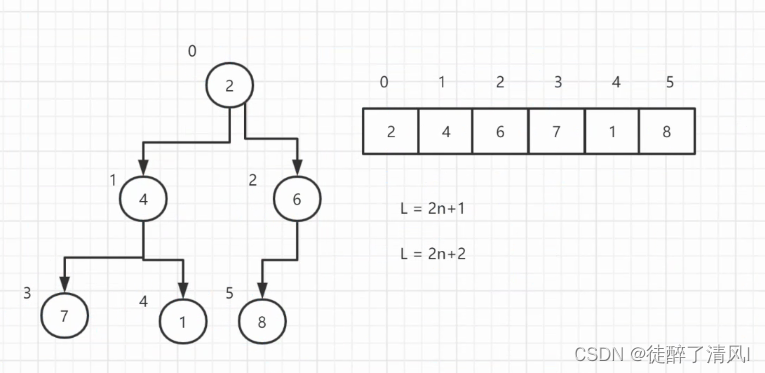
满树 ：除了叶子节点，每层都是满的

完美树 ：除了叶子节点，每个节点都是有两个孩子

哈夫曼树：最优二叉树

 有序树：（左大，右小）

 

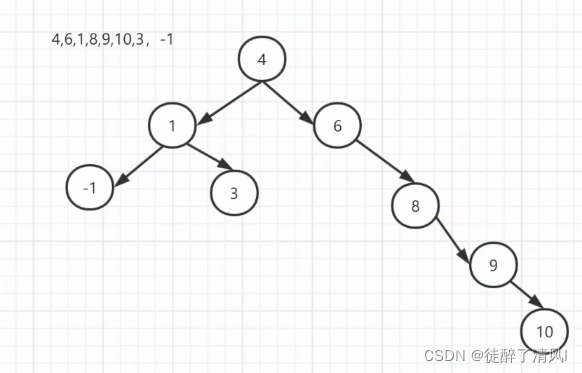
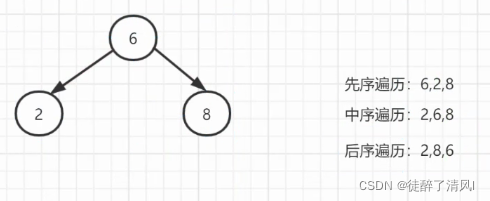
先序 中序 后序

先序遍历：4  1  -1  3  6  8  9  10

中序遍历：-1 1  3  4   6  8  9  10

后序遍历：-1 3 1  10  9  8   6  4

 

平衡树：每个节点左右孩子高度不超过1（红黑树 B类树（B树，B+树））

非平衡树

图

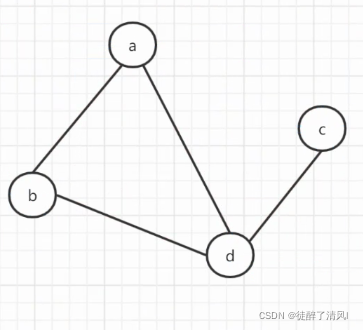
1.无向图

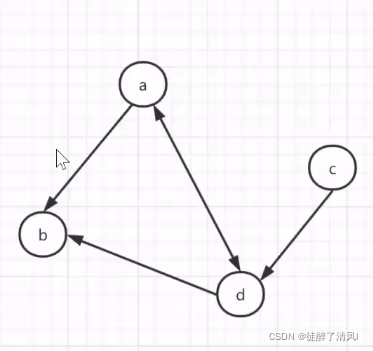
 2.有向图

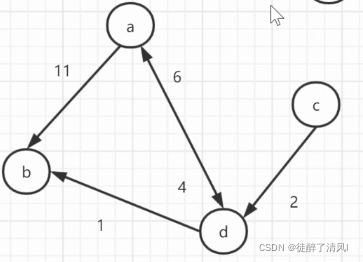
 3.有向带权图